Question
a.Determine the probability generating function for \(X \sim {\text{B}}(1,{\text{ }}p)\).[4]
b.Explain why the probability generating function for \({\text{B}}(n,{\text{ }}p)\) is a polynomial of degree \(n\).[2]
c.Two independent random variables \({X_1}\) and \({X_2}\) are such that \({X_1} \sim {\text{B}}(1,{\text{ }}{p_1})\) and \({X_2} \sim {\text{B}}(1,{\text{ }}{p_2})\). Prove that if \({X_1} + {X_2}\) has a binomial distribution then \({p_1} = {p_2}\).[5]
▶️Answer/Explanation
Markscheme
\({\text{P}}(X = 0) = 1 – p( = q);{\text{ P}}(X = 1) = p\) (M1)(A1)
\({{\text{G}}_x}(t) = \sum\limits_r {{\text{P}}(X = r){t^r}\;\;\;} \)(or writing out term by term) M1
\( = q + pt\) A1
[4 marks]
METHOD 1
\(PGF\) for \(B(n,{\text{ }}p)\) is \({(q + pt)^n}\) R1
which is a polynomial of degree \(n\) R1
METHOD 2
in \(n\) independent trials, it is not possible to obtain more than \(n\) successes (or equivalent, eg, \({\text{P}}(X > n) = 0\)) R1
so \({a_r} = 0\) for \(r > n\) R1
[2 marks]
let \(Y = {X_1} + {X_2}\)
\({G_Y}(t) = ({q_1} + {p_1}t)({q_2} + {p_2}t)\) A1
\({G_Y}(t)\) has degree two, so if \(Y\) is binomial then
\(Y \sim {\text{B}}(2,{\text{ }}p)\) for some \(p\) R1
\({(q + pt)^2} = ({q_1} + {p_1}t)({q_2} + {p_2}t)\) A1
Note: The \(LHS\) could be seen as \({q^2} + 2pqt + {p^2}{t^2}\).
METHOD 1
by considering the roots of both sides, \(\frac{{{q_1}}}{{{p_1}}} = \frac{{{q_2}}}{{{p_2}}}\) M1
\(\frac{{1 – {p_1}}}{{{p_1}}} = \frac{{1 – {p_2}}}{{{p_2}}}\) A1
so \({p_1} = {p_2}\) AG
METHOD 2
equating coefficients,
\({p_1}{p_2} = {p^2},{\text{ }}{q_1}{q_2} = {q^2}{\text{ or }}(1 – {p_1})(1 – {p_2}) = {(1 – p)^2}\) M1
expanding,
\({p_1} + {p_2} = 2p\) so \({p_1},{\text{ }}{p_2}\) are the roots of \({x^2} – 2px + {p^2} = 0\) A1
so \({p_1} = {p_2}\) AG
[5 marks]
Total [11 marks]
Examiners report
Solutions to (a) were often disappointing with some candidates simply writing down the answer. A common error was to forget the possibility of \(X\) being zero so that \(G(t) = pt\) was often seen.
Explanations in (b) were often poor, again indicating a lack of ability to give a verbal explanation.
Very few complete solutions to (c) were seen with few candidates even reaching the result that \(({q_1} + {p_1}t)({q_2} + {p_2}t)\) must equal \({(q + pt)^2}\) for some \(p\).
Question
A continuous random variable \(T\) has a probability density function defined by
\(f(t) = \left\{ {\begin{array}{*{20}{c}} {\frac{{t(4 – {t^2})}}{4}}&{0 \leqslant t \leqslant 2} \\ {0,}&{{\text{otherwise}}} \end{array}} \right.\).
a.Find the cumulative distribution function \(F(t)\), for \(0 \leqslant t \leqslant 2\).[3]
b.i.Sketch the graph of \(F(t)\) for \(0 \leqslant t \leqslant 2\), clearly indicating the coordinates of the endpoints.[2]
b.ii.Given that \(P(T < a) = 0.75\), find the value of \(a\).[2]
▶️Answer/Explanation
Markscheme
\(F(t) = \int_0^t {\left( {x – \frac{{{x^3}}}{4}} \right){\text{d}}x{\text{ }}\left( { = \int_0^t {\frac{{x(4 – {x^2})}}{4}{\text{d}}x} } \right)} \) M1
\( = \left[ {\frac{{{x^2}}}{2} – \frac{{{x^4}}}{{16}}} \right]_0^t{\text{ }}\left( { = \left[ {\frac{{{x^2}(8 – {x^2})}}{{16}}} \right]_0^t} \right){\text{ }}\left( { = \left[ {\frac{{ – 4 – {x^2}{)^2}}}{{16}}} \right]_0^t} \right)\) A1
\( = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}{\text{ }}\left( { = \frac{{{t^2}(8 – {t^2})}}{{16}}} \right){\text{ }}\left( { = 1 – \frac{{{{(4 – {t^2})}^2}}}{{16}}} \right)\) A1
Note: Condone integration involving \(t\) only.
Note: Award M1A0A0 for integration without limits eg, \(\int {\frac{{t(4 – {t^2})}}{4}{\text{d}}t = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}} \) or equivalent.
Note: But allow integration \( + \) \(C\) then showing \(C = 0\) or even integration without \(C\) if \(F(0) = 0\) or \(F(2) = 1\) is confirmed.
[3 marks]
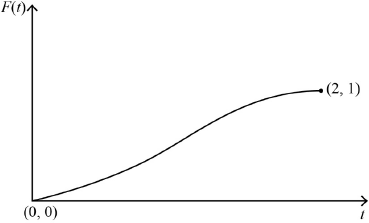
correct shape including correct concavity A1
clearly indicating starts at origin and ends at \((2,{\text{ }}1)\) A1
Note: Condone the absence of \((0,{\text{ }}0)\).
Note: Accept 2 on the \(x\)-axis and 1 on the \(y\)-axis correctly placed.
[2 marks]
attempt to solve \(\frac{{{a^2}}}{2} – \frac{{{a^4}}}{{16}} = 0.75\) (or equivalent) for \(a\) (M1)
\(a = 1.41{\text{ }}( = \sqrt 2 )\) A1
Note: Accept any answer that rounds to 1.4.
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
When Andrew throws a dart at a target, the probability that he hits it is \(\frac{1}{3}\) ; when Bill throws a dart at the target, the probability that he hits the it is \(\frac{1}{4}\) . Successive throws are independent. One evening, they throw darts at the target alternately, starting with Andrew, and stopping as soon as one of their darts hits the target. Let X denote the total number of darts thrown.
a.Write down the value of \({\text{P}}(X = 1)\) and show that \({\text{P}}(X = 2) = \frac{1}{6}\).[2]
b.Show that the probability generating function for X is given by
\[G(t) = \frac{{2t + {t^2}}}{{6 – 3{t^2}}}.\][6]
c.Hence determine \({\text{E}}(X)\).[4]
▶️Answer/Explanation
Markscheme
\({\text{P}}(X = 1) = \frac{1}{3}\) A1
\({\text{P}}(X = 2) = \frac{2}{3} \times \frac{1}{4}\) A1
\(= \frac{1}{6}\) AG
[2 marks]
\(G(t) = \frac{1}{3}t + \frac{2}{3} \times \frac{1}{4}{t^2} + \frac{2}{3} \times \frac{3}{4} \times \frac{1}{3}{t^3} + \frac{2}{3} \times \frac{3}{4} \times \frac{2}{3} \times \frac{1}{4}{t^4} + \ldots \) M1A1
\( = \frac{1}{3}t\left( {1 + \frac{1}{2}{t^2} + \ldots } \right) + \frac{1}{6}{t^2}\left( {1 + \frac{1}{2}{t^2} + \ldots } \right)\) M1A1
\( = \frac{{\frac{t}{3}}}{{1 – \frac{{{t^2}}}{2}}} + \frac{{\frac{{{t^2}}}{6}}}{{1 – \frac{{{t^2}}}{2}}}\) A1A1
\( = \frac{{2t + {t^2}}}{{6 – 3{t^2}}}\) AG
[6 marks]
\(G'(t) = \frac{{(2 + 2t)(6 – 3{t^2}) + 6t(2t + {t^2})}}{{{{(6 – 3{t^2})}^2}}}\) M1A1
\({\text{E}}(X) = G'(1) = \frac{{10}}{3}\) M1A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
