Question
Given the sets \(A\) and \(B\), use the properties of sets to prove that \(A \cup (B’ \cup A)’ = A \cup B\), justifying each step of the proof.
▶️Answer/Explanation
Markscheme
\(A \cup (B’ \cup A)’ = A \cup (B \cap A’)\) De Morgan M1A1
\( = (A \cup B) \cap (A \cup A’)\) Distributive property M1A1
\( = (A \cup B) \cap U\) (Union of set and its complement) A1
\( = A \cup B\) (Intersection with the universal set) AG
Note: Do not accept proofs using Venn diagrams unless the properties are clearly stated.
Note: Accept double inclusion proofs: M1A1 for each inclusion, final A1 for conclusion of equality of sets.
[5 marks]
Examiners report
Question
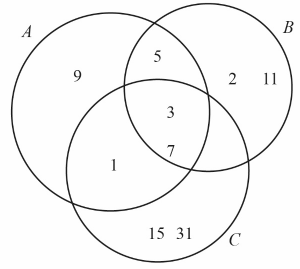
Consider the sets A = {1, 3, 5, 7, 9} , B = {2, 3, 5, 7, 11} and C = {1, 3, 7, 15, 31} .
Find \(\left( {A \cup B} \right) \cap \left( {A \cup C} \right)\).
Verify that A \ C ≠ C \ A.
Let S be a set containing \(n\) elements where \(n \in \mathbb{N}\).
Show that S has \({2^n}\) subsets.
▶️Answer/Explanation
Markscheme
EITHER
\(\left( {A \cup B} \right) \cap \left( {A \cup C} \right) = \left\{ {1,\,2,\,3,\,5,\,7,\,9,\,11} \right\} \cap \left\{ {1,\,3,\,5,\,7,\,9,\,15,\,31} \right\}\) M1A1
OR
\(A \cup \left( {B \cap C} \right) = \left\{ {1,\,3,\,5,\,7,\,9,\,11} \right\} \cup \left\{ {3,\,7} \right\}\) M1A1
OR
\({B \cap C}\) is contained within A (M1)A1
THEN
= {1, 3, 5, 7, 9} (= A) A1
Note: Accept a Venn diagram representation.
[3 marks]
A \ C = {5, 9} A1
C \ A = {15, 31} A1
so A \ C ≠ C \ A AG
Note: Accept a Venn diagram representation.
[2 marks]
METHOD 1
if \(S = \emptyset \) then \(n = 0\) and the number of subsets of S is given by 20 = 1 A1
if \(n > 0\)
for every subset of S, there are 2 possibilities for each element \(x \in S\) either \(x\) will be in the subset or it will not R1
so for all \(n\) elements there are \(\left( {2 \times 2 \times \ldots \times 2} \right){2^n}\) different choices in forming a subset of S R1
so S has \({2^n}\) subsets AG
Note: If candidates attempt induction, award A1 for case \(n = 0\), R1 for setting up the induction method (assume \(P\left( k \right)\) and consider \(P\left( {k + 1} \right)\) and R1 for showing how the \(P\left( k \right)\) true implies \(P\left( {k + 1} \right)\) true).
METHOD 2
\(\sum\limits_{k = 0}^n {\left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)} \) is the number of subsets of S (of all possible sizes from 0 to \(n\)) R1
\({\left( {1 + 1} \right)^n} = \sum\limits_{k = 0}^n {\left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)} \left( {{1^k}} \right)\left( {{1^{n – k}}} \right)\) M1
\({2^n} = \sum\limits_{k = 0}^n {\left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)} \) (= number of subsets of S) A1
so S has \({2^n}\) subsets AG
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
