Question
Prove that \((A \cap B)\backslash (A \cap C) = A \cap (B\backslash C)\) where A, B and C are three subsets of the universal set U.
▶️Answer/Explanation
Markscheme
\((A \cap B)\backslash (A \cap C) = (A \cap B) \cap (A \cap C)’\) M1
\( = (A \cap B) \cap (A’ \cup C’)\) A1
\( = (A \cap B \cap A’) \cup (A \cap B \cap C’)\) A1
\( = (A \cap A’ \cap B) \cup (A \cap B \cap C’)\) A1
\( = (\emptyset \cap B) \cup (A \cap B \cap C’)\) (A1)
\( = \emptyset \cup (A \cap B \cap C’)\)
\( = \left( {A \cap (B \cap C’)} \right)\) A1
\( = A \cap (B\backslash C)\) AG
Note: Do not accept proofs by Venn diagram.
[6 marks]
Examiners report
Venn diagram ‘proof’ are not acceptable. Those who used de Morgan’s laws usually were successful in this question.
Question
\(A\), \(B\), \(C\) and \(D\) are subsets of \(\mathbb{Z}\) .
\(A = \{ \left. m \right|m{\text{ is a prime number less than 15}}\}\)
\(B = \{ \left. m \right|{m^4} = 8m\} \)
\(C = \{ \left. m \right|(m + 1)(m – 2) < 0\} \)
\(D = \{ \left. m \right|{m^2} < 2m + 4\} \)
(a) List the elements of each of these sets.
(b) Determine, giving reasons, which of the following statements are true and which are false.
(i) \(n(D) = n(B) + n(B \cup C)\)
(ii) \(D\backslash B \subset A\)
(iii) \(B \cap A’ = \emptyset \)
(iv) \(n(B\Delta C) = 2\)
▶️Answer/Explanation
Markscheme
(a) by inspection, or otherwise,
A = {2, 3, 5, 7, 11, 13} A1
B = {0, 2} A1
C = {0, 1} A1
D = {–1, 0, 1, 2, 3} A1
[4 marks]
(b) (i) true A1
\(n(B) + n(B \cup C) = 2 + 3 = 5 = n(D)\) R1
(ii) false A1
\(D\backslash B = \{ – 1,{\text{ }}1,{\text{ }}3\} \not\subset A\) R1
(iii) false A1
\(B \cap A’ = \{ 0\} \ne \emptyset \) R1
(iv) true A1
\(n(B\Delta C) = n\{ 1,{\text{ }}2\} = 2\) R1
[8 marks]
Total [12 marks]
Examiners report
It was surprising and disappointing that many candidates regarded 1 as a prime number. One of the consequences of this error was that it simplified some of the set-theoretic calculations in part(b), with a loss of follow-through marks. Generally speaking, it was clear that the majority of candidates were familiar with the set operations in part(b).
Question
Prove that set difference is not associative.
▶️Answer/Explanation
Markscheme
we are trying to prove \((A\backslash B)\backslash C \ne A\backslash (B\backslash C)\) M1(A1)
\({\text{LHS}} = (A \cap B’)\backslash C\) (A1)
\( = (A \cap B’) \cap C’\) A1
\({\text{RHS}} = A\backslash (B \cap C’)\)
\( = A \cap (B \cap C’)’\) (A1)
\( = A \cap (B’ \cup C)\) A1
as LHS does not contain any element of C and RHS does, \({\text{LHS}} \ne {\text{RHS}}\) R1
hence set difference is not associative AG
Note: Accept answers which use a proof containing a counter example.
Total [7 marks]
Examiners report
This question was found difficult by a large number of candidates, but a number of correct solutions were seen. A number of candidates who understood what was required failed to gain the final reasoning mark. Many candidates seemed to be ill-prepared to deal with this style of question.
Question
Consider the set \(A\) consisting of all the permutations of the integers \(1,2,3,4,5\).
a.Two members of \(A\) are given by \(p = (1{\text{ }}2{\text{ }}5)\) and \(q = (1{\text{ }}3)(2{\text{ }}5)\).
Find the single permutation which is equivalent to \(q \circ p\).[4]
b. State a permutation belonging to \(A\) of order
(i) \(4\);
(ii) \(6\).[3]
c.Let \(P = \) {all permutations in \(A\) where exactly two integers change position},
and \(Q = \) {all permutations in \(A\) where the integer \(1\) changes position}.
(i) List all the elements in \(P \cap Q\).
(ii) Find \(n(P \cap Q’)\).[4]
▶️Answer/Explanation
Markscheme
\(q \circ p = (1{\text{ }}3)(2{\text{ }}5)(1{\text{ }}2{\text{ }}5)\) (M1)
\( = (1{\text{ }}5{\text{ }}3)\) M1A1A1
Note: M1 for an answer consisting of disjoint cycles, A1 for \((1{\text{ }}5{\text{ }}3)\),
A1 for either \((2)\) or \((2)\) omitted.
Note: Allow \(\left( {\begin{array}{*{20}{c}} 1&2&3&4&5 \\ 5&2&1&4&3 \end{array}} \right)\)
If done in the wrong order and obtained \((1{\text{ }}3{\text{ }}2)\), award A2.
[4 marks]
(i) any cycle with length \(4\) eg (\(1234\)) A1
(ii) any permutation with \(2\) disjoint cycles one of length \(2\) and one of length \(3\) eg (\(1\) \(2\)) (\(3\) \(4\) \(5\)) M1A1
Note: Award M1A0 for any permutation with \(2\) non-disjoint cycles one of length \(2\) and one of length \(3\).
Accept non cycle notation.
[3 marks]
(i) (\(1\), \(2\)), (\(1\), \(3\)), (\(1\), \(4\)), (\(1\), \(5\)) M1A1
(ii) (\(2\) \(3\)), (\(2\) \(4\)), (\(2\) \(5\)), (\(3\) \(4\)), (\(3\) \(5\)), (\(4\) \(5\)) (M1)
6 A1
Note: Award M1 for at least one correct cycle.
[4 marks]
Total [11 marks]
Examiners report
Many students were unable to start the question, seemingly as they did not understand the cyclic notation. Many of those that did understand found it quite straightforward to obtain good marks on this question.
Many students were unable to start the question, seemingly as they did not understand the cyclic notation. Many of those that did understand found it quite straightforward to obtain good marks on this question.
Many students were unable to start the question, seemingly as they did not understand the cyclic notation. Many of those that did understand found it quite straightforward to obtain good marks on this question.
Question
Given the sets \(A\) and \(B\), use the properties of sets to prove that \(A \cup (B’ \cup A)’ = A \cup B\), justifying each step of the proof.
▶️Answer/Explanation
Markscheme
\(A \cup (B’ \cup A)’ = A \cup (B \cap A’)\) De Morgan M1A1
\( = (A \cup B) \cap (A \cup A’)\) Distributive property M1A1
\( = (A \cup B) \cap U\) (Union of set and its complement) A1
\( = A \cup B\) (Intersection with the universal set) AG
Note: Do not accept proofs using Venn diagrams unless the properties are clearly stated.
Note: Accept double inclusion proofs: M1A1 for each inclusion, final A1 for conclusion of equality of sets.
[5 marks]
Examiners report
Question
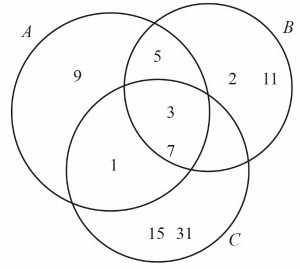
Consider the sets A = {1, 3, 5, 7, 9} , B = {2, 3, 5, 7, 11} and C = {1, 3, 7, 15, 31} .
a.i.Find \(\left( {A \cup B} \right) \cap \left( {A \cup C} \right)\).[3]
a.ii.Verify that A \ C ≠ C \ A.[2]
b.Let S be a set containing \(n\) elements where \(n \in \mathbb{N}\).
Show that S has \({2^n}\) subsets.[3]
▶️Answer/Explanation
Markscheme
EITHER
\(\left( {A \cup B} \right) \cap \left( {A \cup C} \right) = \left\{ {1,\,2,\,3,\,5,\,7,\,9,\,11} \right\} \cap \left\{ {1,\,3,\,5,\,7,\,9,\,15,\,31} \right\}\) M1A1
OR
\(A \cup \left( {B \cap C} \right) = \left\{ {1,\,3,\,5,\,7,\,9,\,11} \right\} \cup \left\{ {3,\,7} \right\}\) M1A1
OR
\({B \cap C}\) is contained within A (M1)A1
THEN
= {1, 3, 5, 7, 9} (= A) A1
Note: Accept a Venn diagram representation.
[3 marks]
A \ C = {5, 9} A1
C \ A = {15, 31} A1
so A \ C ≠ C \ A AG
Note: Accept a Venn diagram representation.
[2 marks]
METHOD 1
if \(S = \emptyset \) then \(n = 0\) and the number of subsets of S is given by 20 = 1 A1
if \(n > 0\)
for every subset of S, there are 2 possibilities for each element \(x \in S\) either \(x\) will be in the subset or it will not R1
so for all \(n\) elements there are \(\left( {2 \times 2 \times \ldots \times 2} \right){2^n}\) different choices in forming a subset of S R1
so S has \({2^n}\) subsets AG
Note: If candidates attempt induction, award A1 for case \(n = 0\), R1 for setting up the induction method (assume \(P\left( k \right)\) and consider \(P\left( {k + 1} \right)\) and R1 for showing how the \(P\left( k \right)\) true implies \(P\left( {k + 1} \right)\) true).
METHOD 2
\(\sum\limits_{k = 0}^n {\left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)} \) is the number of subsets of S (of all possible sizes from 0 to \(n\)) R1
\({\left( {1 + 1} \right)^n} = \sum\limits_{k = 0}^n {\left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)} \left( {{1^k}} \right)\left( {{1^{n – k}}} \right)\) M1
\({2^n} = \sum\limits_{k = 0}^n {\left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)} \) (= number of subsets of S) A1
so S has \({2^n}\) subsets AG
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
