Question
The permutation \({p_1}\) of the set {1, 2, 3, 4} is defined by
\[{p_1} = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
2&4&1&3
\end{array}} \right)\]
(a) (i) State the inverse of \({p_1}\).
(ii) Find the order of \({p_1}\).
(b) Another permutation \({p_2}\) is defined by
\[{p_2} = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
3&2&4&1
\end{array}} \right)\]
(i) Determine whether or not the composition of \({p_1}\) and \({p_2}\) is commutative.
(ii) Find the permutation \({p_3}\) which satisfies
\[{p_1}{p_3}{p_2} = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
1&2&3&4
\end{array}} \right){\text{.}}\]
▶️Answer/Explanation
Markscheme
(a) (i) the inverse is
\(\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
3&1&4&2
\end{array}} \right)\) A1
(ii) EITHER
\(1 \to 2 \to 4 \to 3 \to 1\) (is a cycle of length 4) R3
so \({p_1}\) is of order 4 A1 N2
OR
consider
\(p_1^2 = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
4&3&1&2
\end{array}} \right)\) M1A1
it is now clear that
\(p_1^4 = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
1&2&3&4
\end{array}} \right)\) A1
so \({p_1}\) is of order 4 A1 N2
[5 marks]
(b) (i) consider
\({p_1}{p_2} = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
2&4&1&3
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
3&2&4&1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
1&4&3&2
\end{array}} \right)\) M1A1
\({p_2}{p_1} = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
3&2&4&1
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
2&4&1&3
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
2&1&3&4
\end{array}} \right)\) A1
composition is not commutative A1
Note: In this part do not penalize candidates who incorrectly reverse the order both times.
(ii) EITHER
pre and postmultiply by \(p_1^{ – 1}\), \(p_2^{ – 1}\)to give
\({p_3} = p_1^{ – 1}p_2^{ – 1}\) (M1)(A1)
\( = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
3&1&4&2
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
4&2&1&3
\end{array}} \right)\) A1
\( = \left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
2&1&3&4
\end{array}} \right)\) A1
OR
starting from
\(\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
2&4&1&3
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
{}&{}&{}&{}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
3&2&4&1
\end{array}} \right)\) M1
successively deducing each missing number, to get
\(\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
2&4&1&3
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
2&1&3&4
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
1&2&3&4 \\
3&2&4&1
\end{array}} \right)\) A3
[8 marks]
Total [13 marks]
Examiners report
Many candidates scored well on this question although some gave the impression of not having studied this topic. The most common error in (b) was to believe incorrectly that \({p_1}{p_2}\) means \({p_1}\) followed by \({p_2}\). This was condoned in (i) but penalised in (ii). The Guide makes it quite clear that this is the notation to be used.
Question
Let \(\{ G,{\text{ }} \circ \} \) be the group of all permutations of \(1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6\) under the operation of composition of permutations.
Consider the following Venn diagram, where \(A = \{ 1,{\text{ }}2,{\text{ }}3,{\text{ }}4\} ,{\text{ }}B = \{ 3,{\text{ }}4,{\text{ }}5,{\text{ }}6\} \).
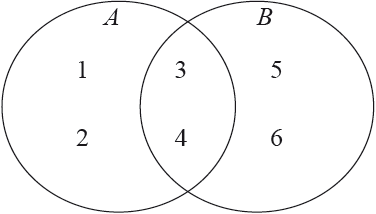
a.(i) Write the permutation \(\alpha = \left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 3&4&6&2&1&5 \end{array}} \right)\) as a composition of disjoint cycles.
(ii) State the order of \(\alpha \).[3]
b.(i) Write the permutation \(\beta = \left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 6&4&3&5&1&2 \end{array}} \right)\) as a composition of disjoint cycles.
(ii) State the order of \(\beta \).[2]
c.Write the permutation \(\alpha \circ \beta \) as a composition of disjoint cycles.[2]
d.Write the permutation \(\beta \circ \alpha \) as a composition of disjoint cycles.[2]
e.State the order of \(\{ G,{\text{ }} \circ \} \).[2]
f.Find the number of permutations in \(\{ G,{\text{ }} \circ \} \) which will result in \(A\), \(B\) and \(A \cap B\) remaining unchanged.[2]
▶️Answer/Explanation
Markscheme
(i) \((1{\text{ }}3{\text{ }}6{\text{ }}5)(2{\text{ }}4)\) A1A1
(ii) 4 A1
Note: In (b) (c) and (d) single cycles can be omitted.
[3 marks]
(i) \((1{\text{ }}6{\text{ }}2{\text{ }}4{\text{ }}5)(3)\) A1
(ii) 5 A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 5&2&6&1&3&4 \end{array}} \right) = (1{\text{ }}5{\text{ }}3{\text{ }}6{\text{ }}4)(2)\) (M1)A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 3&5&2&4&6&1 \end{array}} \right) = (1{\text{ }}3{\text{ }}2{\text{ }}5{\text{ }}6)(4)\) (M1)A1
Note: Award A2A0 for (c) and (d) combined, if answers are the wrong way round.
[2 marks]
\(6! = 720\) A2
[2 marks]
any composition of the cycles (1 2), (3 4) and (5 6) (M1)
so \({2^3} = 8\) A1
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Let \(\{ G,{\text{ }} \circ \} \) be the group of all permutations of \(1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6\) under the operation of composition of permutations.
Consider the following Venn diagram, where \(A = \{ 1,{\text{ }}2,{\text{ }}3,{\text{ }}4\} ,{\text{ }}B = \{ 3,{\text{ }}4,{\text{ }}5,{\text{ }}6\} \).

a.(i) Write the permutation \(\alpha = \left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 3&4&6&2&1&5 \end{array}} \right)\) as a composition of disjoint cycles.
(ii) State the order of \(\alpha \).[3]
b.(i) Write the permutation \(\beta = \left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 6&4&3&5&1&2 \end{array}} \right)\) as a composition of disjoint cycles.
(ii) State the order of \(\beta \).[2]
c.Write the permutation \(\alpha \circ \beta \) as a composition of disjoint cycles.[2]
d.Write the permutation \(\beta \circ \alpha \) as a composition of disjoint cycles.[2]
e.State the order of \(\{ G,{\text{ }} \circ \} \).[2]
f.Find the number of permutations in \(\{ G,{\text{ }} \circ \} \) which will result in \(A\), \(B\) and \(A \cap B\) remaining unchanged.[2]
▶️Answer/Explanation
Markscheme
(i) \((1{\text{ }}3{\text{ }}6{\text{ }}5)(2{\text{ }}4)\) A1A1
(ii) 4 A1
Note: In (b) (c) and (d) single cycles can be omitted.
[3 marks]
(i) \((1{\text{ }}6{\text{ }}2{\text{ }}4{\text{ }}5)(3)\) A1
(ii) 5 A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 5&2&6&1&3&4 \end{array}} \right) = (1{\text{ }}5{\text{ }}3{\text{ }}6{\text{ }}4)(2)\) (M1)A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 3&5&2&4&6&1 \end{array}} \right) = (1{\text{ }}3{\text{ }}2{\text{ }}5{\text{ }}6)(4)\) (M1)A1
Note: Award A2A0 for (c) and (d) combined, if answers are the wrong way round.
[2 marks]
\(6! = 720\) A2
[2 marks]
any composition of the cycles (1 2), (3 4) and (5 6) (M1)
so \({2^3} = 8\) A1
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
The set of all permutations of the list of the integers 1, 2, 3 4 is a group, S4, under the operation of function composition.
In the group S4 let \({p_1} = \left( \begin{gathered}
\begin{array}{*{20}{c}}
1&2&3&4
\end{array} \hfill \\
\begin{array}{*{20}{c}}
2&3&1&4
\end{array} \hfill \\
\end{gathered} \right)\) and \({p_2} = \left( \begin{gathered}
\begin{array}{*{20}{c}}
1&2&3&4
\end{array} \hfill \\
\begin{array}{*{20}{c}}
2&1&3&4
\end{array} \hfill \\
\end{gathered} \right)\).
a.Determine the order of S4.[2]
b.Find the proper subgroup H of order 6 containing \({p_1}\), \({p_2}\) and their compositions. Express each element of H in cycle form.[5]
c.Let \(f{\text{:}}\,{S_4} \to {S_4}\) be defined by \(f\left( p \right) = p \circ p\) for \(p \in {S_4}\).
Using \({p_1}\) and \({p_2}\), explain why \(f\) is not a homomorphism.[5]
▶️Answer/Explanation
Markscheme
number of possible permutations is 4 × 3 × 2 × 1 (M1)
= 24(= 4!) A1
[2 marks]
attempting to find one of \({p_1} \circ {p_1}\), \({p_1} \circ {p_2}\) or \({p_2} \circ {p_1}\) M1
\({p_1} \circ {p_1} = \left( {132} \right)\) or equivalent (eg, \({p_1}^{ – 1} = \left( {132} \right)\)) A1
\( {p_1} \circ {p_2} = \left( {13} \right)\) or equivalent (eg, \({p_2} \circ {p_1} \circ {p_1} = \left( {13} \right)\)) A1
\({p_2} \circ {p_1} = \left( {23} \right)\) or equivalent (eg, \({p_1} \circ {p_1} \circ {p_2} = \left( {23} \right)\)) A1
Note: Award A1A0A0 for one correct permutation in any form; A1A1A0 for two correct permutations in any form.
\(e = \left( 1 \right)\), \({p_1} = \left( {123} \right)\) and \({p_2} = \left( {12} \right)\) A1
Note: Condone omission of identity in cycle form as long as it is clear it is considered one of the elements of H.
[5 marks]
METHOD 1
if \(f\) is a homomorphism \(f\left( {{p_1} \circ {p_2}} \right) = f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\)
attempting to express one of \(f\left( {{p_1} \circ {p_2}} \right)\) or \(f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\) in terms of \({p_1}\) and \({p_2}\) M1
\(f\left( {{p_1} \circ {p_2}} \right) = {p_1} \circ {p_2} \circ {p_1} \circ {p_2}\) A1
\(f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right) = {p_1} \circ {p_1} \circ {p_2} \circ {p_2}\) A1
\( \Rightarrow {p_2} \circ {p_1} = {p_1} \circ {p_2}\) A1
but \({p_1} \circ {p_2} \ne {p_2} \circ {p_1}\) R1
so \(f\) is not a homomorphism AG
Note: Award R1 only if M1 is awarded.
Note: Award marks only if \({p_1}\) and \({p_2}\) are used; cycle form is not required.
METHOD 2
if \(f\) is a homomorphism \(f\left( {{p_1} \circ {p_2}} \right) = f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\)
attempting to find one of \(f\left( {{p_1} \circ {p_2}} \right)\) or \(f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\) M1
\(f\left( {{p_1} \circ {p_2}} \right) = e\) A1
\(f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right) = \left( {132} \right)\) (M1)A1
so \(f\left( {{p_1} \circ {p_2}} \right) \ne f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\) R1
so \(f\) is not a homomorphism AG
Note: Award R1 only if M1 is awarded.
Note: Award marks only if \({p_1}\) and \({p_2}\) are used; cycle form is not required.
[5 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
The group \(\{ G,{\text{ }}{ \times _7}\} \) is defined on the set {1, 2, 3, 4, 5, 6} where \({ \times _7}\) denotes multiplication modulo 7.
a.(i) Write down the Cayley table for \(\{ G,{\text{ }}{ \times _7}\} \) .
(ii) Determine whether or not \(\{ G,{\text{ }}{ \times _7}\} \) is cyclic.
(iii) Find the subgroup of G of order 3, denoting it by H .
(iv) Identify the element of order 2 in G and find its coset with respect to H .[10]
b.The group \(\{ K,{\text{ }} \circ \} \) is defined on the six permutations of the integers 1, 2, 3 and \( \circ \) denotes composition of permutations.
(i) Show that \(\{ K,{\text{ }} \circ \} \) is non-Abelian.
(ii) Giving a reason, state whether or not \(\{ G,{\text{ }}{ \times _7}\} \) and \(\{ K,{\text{ }} \circ \} \) are isomorphic.[6]
▶️Answer/Explanation
Markscheme
(i) the Cayley table is
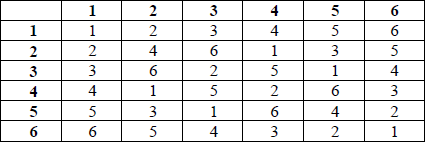 A3
A3
Note: Deduct 1 mark for each error up to a maximum of 3.
(ii) by considering powers of elements, (M1)
it follows that 3 (or 5) is of order 6 A1
so the group is cyclic A1
(iii) we see that 2 and 4 are of order 3 so the subgroup of order 3 is {1, 2, 4} M1A1
(iv) the element of order 2 is 6 A1
the coset is {3, 5, 6} A1
[10 marks]
(i) consider for example
\(\left( {\begin{array}{*{20}{c}}
1&2&3 \\
2&1&3
\end{array}} \right) \circ \left( {\begin{array}{*{20}{c}}
1&2&3 \\
2&3&1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1&2&3 \\
1&3&2
\end{array}} \right)\) M1A1
\(\left( {\begin{array}{*{20}{c}}
1&2&3 \\
2&3&1
\end{array}} \right) \circ \left( {\begin{array}{*{20}{c}}
1&2&3 \\
2&1&3
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1&2&3 \\
3&2&1
\end{array}} \right)\) M1A1
Note: Award M1A1M1A0 if both compositions are done in the wrong order.
Note: Award M1A1M0A0 if the two compositions give the same result, if no further attempt is made to find two permutations which are not commutative.
these are different so the group is not Abelian R1AG
(ii) they are not isomorphic because \(\{ G,{\text{ }}{ \times _7}\} \) is Abelian and \(\{ K,{\text{ }} \circ \} \) is not R1
[6 marks]
Examiners report
[N/A]
[N/A]
