Question
The set of all permutations of the list of the integers 1, 2, 3 4 is a group, S4, under the operation of function composition.
In the group S4 let \({p_1} = \left( \begin{gathered}
\begin{array}{*{20}{c}}
1&2&3&4
\end{array} \hfill \\
\begin{array}{*{20}{c}}
2&3&1&4
\end{array} \hfill \\
\end{gathered} \right)\) and \({p_2} = \left( \begin{gathered}
\begin{array}{*{20}{c}}
1&2&3&4
\end{array} \hfill \\
\begin{array}{*{20}{c}}
2&1&3&4
\end{array} \hfill \\
\end{gathered} \right)\).
a.Determine the order of S4.[2]
b.Find the proper subgroup H of order 6 containing \({p_1}\), \({p_2}\) and their compositions. Express each element of H in cycle form.[5]
c.Let \(f{\text{:}}\,{S_4} \to {S_4}\) be defined by \(f\left( p \right) = p \circ p\) for \(p \in {S_4}\).
Using \({p_1}\) and \({p_2}\), explain why \(f\) is not a homomorphism.[5]
▶️Answer/Explanation
Markscheme
number of possible permutations is 4 × 3 × 2 × 1 (M1)
= 24(= 4!) A1
[2 marks]
attempting to find one of \({p_1} \circ {p_1}\), \({p_1} \circ {p_2}\) or \({p_2} \circ {p_1}\) M1
\({p_1} \circ {p_1} = \left( {132} \right)\) or equivalent (eg, \({p_1}^{ – 1} = \left( {132} \right)\)) A1
\( {p_1} \circ {p_2} = \left( {13} \right)\) or equivalent (eg, \({p_2} \circ {p_1} \circ {p_1} = \left( {13} \right)\)) A1
\({p_2} \circ {p_1} = \left( {23} \right)\) or equivalent (eg, \({p_1} \circ {p_1} \circ {p_2} = \left( {23} \right)\)) A1
Note: Award A1A0A0 for one correct permutation in any form; A1A1A0 for two correct permutations in any form.
\(e = \left( 1 \right)\), \({p_1} = \left( {123} \right)\) and \({p_2} = \left( {12} \right)\) A1
Note: Condone omission of identity in cycle form as long as it is clear it is considered one of the elements of H.
[5 marks]
METHOD 1
if \(f\) is a homomorphism \(f\left( {{p_1} \circ {p_2}} \right) = f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\)
attempting to express one of \(f\left( {{p_1} \circ {p_2}} \right)\) or \(f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\) in terms of \({p_1}\) and \({p_2}\) M1
\(f\left( {{p_1} \circ {p_2}} \right) = {p_1} \circ {p_2} \circ {p_1} \circ {p_2}\) A1
\(f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right) = {p_1} \circ {p_1} \circ {p_2} \circ {p_2}\) A1
\( \Rightarrow {p_2} \circ {p_1} = {p_1} \circ {p_2}\) A1
but \({p_1} \circ {p_2} \ne {p_2} \circ {p_1}\) R1
so \(f\) is not a homomorphism AG
Note: Award R1 only if M1 is awarded.
Note: Award marks only if \({p_1}\) and \({p_2}\) are used; cycle form is not required.
METHOD 2
if \(f\) is a homomorphism \(f\left( {{p_1} \circ {p_2}} \right) = f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\)
attempting to find one of \(f\left( {{p_1} \circ {p_2}} \right)\) or \(f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\) M1
\(f\left( {{p_1} \circ {p_2}} \right) = e\) A1
\(f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right) = \left( {132} \right)\) (M1)A1
so \(f\left( {{p_1} \circ {p_2}} \right) \ne f\left( {{p_1}} \right) \circ f\left( {{p_2}} \right)\) R1
so \(f\) is not a homomorphism AG
Note: Award R1 only if M1 is awarded.
Note: Award marks only if \({p_1}\) and \({p_2}\) are used; cycle form is not required.
[5 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Let \(\{ G,{\text{ }} \circ \} \) be the group of all permutations of \(1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6\) under the operation of composition of permutations.
Consider the following Venn diagram, where \(A = \{ 1,{\text{ }}2,{\text{ }}3,{\text{ }}4\} ,{\text{ }}B = \{ 3,{\text{ }}4,{\text{ }}5,{\text{ }}6\} \).
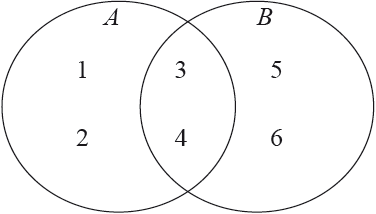
a.(i) Write the permutation \(\alpha = \left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 3&4&6&2&1&5 \end{array}} \right)\) as a composition of disjoint cycles.
(ii) State the order of \(\alpha \).[3]
b.(i) Write the permutation \(\beta = \left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 6&4&3&5&1&2 \end{array}} \right)\) as a composition of disjoint cycles.
(ii) State the order of \(\beta \).[2]
c.Write the permutation \(\alpha \circ \beta \) as a composition of disjoint cycles.[2]
d.Write the permutation \(\beta \circ \alpha \) as a composition of disjoint cycles.[2]
e.State the order of \(\{ G,{\text{ }} \circ \} \).[2]
f.Find the number of permutations in \(\{ G,{\text{ }} \circ \} \) which will result in \(A\), \(B\) and \(A \cap B\) remaining unchanged.[2]
▶️Answer/Explanation
Markscheme
(i) \((1{\text{ }}3{\text{ }}6{\text{ }}5)(2{\text{ }}4)\) A1A1
(ii) 4 A1
Note: In (b) (c) and (d) single cycles can be omitted.
[3 marks]
(i) \((1{\text{ }}6{\text{ }}2{\text{ }}4{\text{ }}5)(3)\) A1
(ii) 5 A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 5&2&6&1&3&4 \end{array}} \right) = (1{\text{ }}5{\text{ }}3{\text{ }}6{\text{ }}4)(2)\) (M1)A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 3&5&2&4&6&1 \end{array}} \right) = (1{\text{ }}3{\text{ }}2{\text{ }}5{\text{ }}6)(4)\) (M1)A1
Note: Award A2A0 for (c) and (d) combined, if answers are the wrong way round.
[2 marks]
\(6! = 720\) A2
[2 marks]
any composition of the cycles (1 2), (3 4) and (5 6) (M1)
so \({2^3} = 8\) A1
[2 marks]
Question
The set of all permutations of the elements \(1,{\text{ }}2,{\text{ }} \ldots 10\) is denoted by \(H\) and the binary operation \( \circ \) represents the composition of permutations.
The permutation \(p = (1{\text{ }}2{\text{ }}3{\text{ }}4{\text{ }}5{\text{ }}6)(7{\text{ }}8{\text{ }}9{\text{ }}10)\) generates the subgroup \(\{ G,{\text{ }} \circ \} \) of the group \(\{ H,{\text{ }} \circ \} \).
a.Find the order of \(\{ G,{\text{ }} \circ \} \).[2]
b.State the identity element in \(\{ G,{\text{ }} \circ \} \).[1]
c.Find
(i) \(p \circ p\);
(ii) the inverse of \(p \circ p\).[4]
d.(i) Find the maximum possible order of an element in \(\{ H,{\text{ }} \circ \} \).
(ii) Give an example of an element with this order.[3]
▶️Answer/Explanation
Markscheme
the order of \((G,{\text{ }} \circ )\) is \({\text{lcm}}(6,{\text{ }}4)\) (M1)
\( = 12\) A1
[2 marks]
\(\left( 1 \right){\rm{ }}\left( 2 \right){\rm{ }}\left( 3 \right){\rm{ }}\left( 4 \right){\rm{ }}\left( 5 \right){\rm{ }}\left( 6 \right){\rm{ }}\left( 7 \right){\rm{ }}\left( 8 \right){\rm{ }}\left( 9 \right){\rm{ }}\left( {10} \right)\) A1
Note: Accept ( ) or a word description.
[1 mark]
(i) \(p \circ p = (1{\text{ }}3{\text{ }}5)(2{\text{ }}4{\text{ }}6)(7{\text{ }}9)(810)\) (M1)A1
(ii) its inverse \( = (1{\text{ }}5{\text{ }}3)(2{\text{ }}6{\text{ }}4)(7{\text{ }}9)(810)\) A1A1
Note: Award A1 for cycles of 2, A1 for cycles of 3.
[4 marks]
(i) considering LCM of length of cycles with length \(2\), \(3\) and \(5\) (M1)
\(30\) A1
(ii) eg\(\;\;\;(1{\text{ }}2)(3{\text{ }}4{\text{ }}5)(6{\text{ }}7{\text{ }}8{\text{ }}9{\text{ }}10)\) A1
Note: allow FT as long as the length of cycles adds to \(10\) and their LCM is consistent with answer to part (i).
Note: Accept alternative notation for each part
[3 marks]
Total [10 marks]
