Question
H and K are subgroups of a group G. By considering the four group axioms, prove that \(H \cap K\) is also a subgroup of G.
▶️Answer/Explanation
Markscheme
closure: let \(a,{\text{ }}b \in H \cap K\), so that \(a,{\text{ }}b \in H\) and \(a,{\text{ }}b \in K\) M1
therefore \(ab \in H\) and \(ab \in K\) so that \(ab \in H \cap K\) A1
associativity: this carries over from G R1
identity: the identity \(e \in H\) and \(e \in K\) M1
therefore \(e \in H \cap K\) A1
inverse:
\(a \in H \cap K\) implies \(a \in H\) and \(a \in K\) M1
it follows that \({a^{ – 1}} \in H\) and \({a^{ – 1}} \in K\) A1
and therefore that \({a^{ – 1}} \in H \cap K\) A1
the four group axioms are therefore satisfied AG
[8 marks]
Examiners report
This question presented the most difficulty for students. Overall the candidates showed a lack of ability to present a formal proof. Some gained points for the proof of the identity element in the intersection and the statement that the associative property carries over from the group. However, the vast majority gained no points for the proof of closure or the inverse axioms.
Question
The set of all permutations of the elements \(1,{\text{ }}2,{\text{ }} \ldots 10\) is denoted by \(H\) and the binary operation \( \circ \) represents the composition of permutations.
The permutation \(p = (1{\text{ }}2{\text{ }}3{\text{ }}4{\text{ }}5{\text{ }}6)(7{\text{ }}8{\text{ }}9{\text{ }}10)\) generates the subgroup \(\{ G,{\text{ }} \circ \} \) of the group \(\{ H,{\text{ }} \circ \} \).
a.Find the order of \(\{ G,{\text{ }} \circ \} \).[2]
b.State the identity element in \(\{ G,{\text{ }} \circ \} \).[1]
c.Find
(i) \(p \circ p\);
(ii) the inverse of \(p \circ p\).[4]
d.(i) Find the maximum possible order of an element in \(\{ H,{\text{ }} \circ \} \).
(ii) Give an example of an element with this order.[3]
▶️Answer/Explanation
Markscheme
the order of \((G,{\text{ }} \circ )\) is \({\text{lcm}}(6,{\text{ }}4)\) (M1)
\( = 12\) A1
[2 marks]
\(\left( 1 \right){\rm{ }}\left( 2 \right){\rm{ }}\left( 3 \right){\rm{ }}\left( 4 \right){\rm{ }}\left( 5 \right){\rm{ }}\left( 6 \right){\rm{ }}\left( 7 \right){\rm{ }}\left( 8 \right){\rm{ }}\left( 9 \right){\rm{ }}\left( {10} \right)\) A1
Note: Accept ( ) or a word description.
[1 mark]
(i) \(p \circ p = (1{\text{ }}3{\text{ }}5)(2{\text{ }}4{\text{ }}6)(7{\text{ }}9)(810)\) (M1)A1
(ii) its inverse \( = (1{\text{ }}5{\text{ }}3)(2{\text{ }}6{\text{ }}4)(7{\text{ }}9)(810)\) A1A1
Note: Award A1 for cycles of 2, A1 for cycles of 3.
[4 marks]
(i) considering LCM of length of cycles with length \(2\), \(3\) and \(5\) (M1)
\(30\) A1
(ii) eg\(\;\;\;(1{\text{ }}2)(3{\text{ }}4{\text{ }}5)(6{\text{ }}7{\text{ }}8{\text{ }}9{\text{ }}10)\) A1
Note: allow FT as long as the length of cycles adds to \(10\) and their LCM is consistent with answer to part (i).
Note: Accept alternative notation for each part
[3 marks]
Total [10 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
The group \(\{ G,{\text{ }} * \} \) is defined on the set \(G\) with binary operation \( * \). \(H\) is a subset of \(G\) defined by \(H = \{ x:{\text{ }}x \in G,{\text{ }}a * x * {a^{ – 1}} = x{\text{ for all }}a \in G\} \). Prove that \(\{ H,{\text{ }} * \} \) is a subgroup of \(\{ G,{\text{ }} * \} \).
▶️Answer/Explanation
Markscheme
associativity: This follows from associativity in \(\{ G,{\text{ }} * \} \) R1
the identity \(e \in H\) since \(a * e * {a^{ – 1}} = a * {a^{ – 1}} = e\) (for all \(a \in G\)) R1
Note: Condone the use of the commutativity of e if that is involved in an alternative simplification of the LHS.
closure: Let \(x,{\text{ }}y \in H\) so that \(a * x * {a^{ – 1}} = x\) and \(a * y * {a^{ – 1}} = y\) for all \(a \in G\) (M1)
multiplying, \(x * y = a * x * {a^{ – 1}} * a * y * {a^{ – 1}}\) (for all \(a \in G\)) A1
\( = a * x * y * {a^{ – 1}}\) A1
therefore \(x * y \in H\) (proving closure) R1
inverse: Let \(x \in H\) so that \(a * x * {a^{ – 1}} = x\) (for all \(a \in G\))
\({x^{ – 1}} = {(a * x * {a^{ – 1}})^{ – 1}}\) M1
\( = a * {x^{ – 1}} * {a^{ – 1}}\) A1
therefore \({x^{ – 1}} \in H\) R1
hence \(\{ H,{\text{ }} * \} \) is a subgroup of \(\{ G,{\text{ }} * \} \) AG
Note: Accuracy marks cannot be awarded if commutativity is assumed for general elements of \(G\).
[9 marks]
Examiners report
This is an abstract question, clearly defined on a subset. Far too many candidates almost immediately deduced, erroneously, that the full group was Abelian. Almost no marks were then available.
Question
Consider the group \(\{ G,{\text{ }}{ \times _{18}}\} \) defined on the set \(\{ 1,{\text{ }}5,{\text{ }}7,{\text{ }}11,{\text{ }}13,{\text{ }}17\} \) where \({ \times _{18}}\) denotes multiplication modulo 18. The group \(\{ G,{\text{ }}{ \times _{18}}\} \) is shown in the following Cayley table.
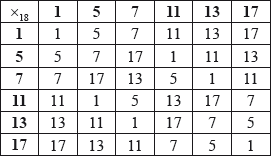
The subgroup of \(\{ G,{\text{ }}{ \times _{18}}\} \) of order two is denoted by \(\{ K,{\text{ }}{ \times _{18}}\} \).
a.i.Find the order of elements 5, 7 and 17 in \(\{ G,{\text{ }}{ \times _{18}}\} \).[4]
a.ii.State whether or not \(\{ G,{\text{ }}{ \times _{18}}\} \) is cyclic, justifying your answer.[2]
b.Write down the elements in set \(K\).[1]
c.Find the left cosets of \(K\) in \(\{ G,{\text{ }}{ \times _{18}}\} \).[4]
▶️Answer/Explanation
Markscheme
considering powers of elements (M1)
5 has order 6 A1
7 has order 3 A1
17 has order 2 A1
[4 marks]
\(G\) is cyclic A1
because there is an element (are elements) of order 6 R1
Note: Accept “there is a generator”; allow A1R0.
[3 marks]
\(\{ 1,{\text{ }}17\} \) A1
[1 mark]
multiplying \(\{ 1,{\text{ }}17\} \) by each element of \(G\) (M1)
\(\{ 1,{\text{ }}17\} ,{\text{ }}\{ 5,{\text{ }}13\} ,{\text{ }}\{ 7,{\text{ }}11\} \) A1A1A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
Let \(\{ G,{\text{ }} * \} \) be a finite group and let H be a non-empty subset of G . Prove that \(\{ H,{\text{ }} * \} \) is a group if H is closed under \( * \).
▶️Answer/Explanation
Markscheme
the associativity property carries over from G R1
closure is given R1
let \(h \in H\) and let n denote the order of h, (this is finite because G is finite) M1
it follows that \({h^n} = e\), the identity element R1
and since H is closed, \(e \in H\) R1
since \(h * {h^{n – 1}} = e\) M1
it follows that \({h^{n – 1}}\) is the inverse, \({h^{ – 1}}\), of h R1
and since H is closed, \({h^{ – 1}} \in H\) so each element of H has an inverse element R1
the four requirements for H to be a group are therefore satisfied AG
[8 marks]
