Question
Let \(f:G \to H\) be a homomorphism of finite groups.
a.Prove that \(f({e_G}) = {e_H}\), where \({e_G}\) is the identity element in \(G\) and \({e_H}\) is the identity
element in \(H\).[2]
b.(i) Prove that the kernel of \(f,{\text{ }}K = {\text{Ker}}(f)\), is closed under the group operation.
(ii) Deduce that \(K\) is a subgroup of \(G\).[6]
c.(i) Prove that \(gk{g^{ – 1}} \in K\) for all \(g \in G,{\text{ }}k \in K\).
(ii) Deduce that each left coset of K in G is also a right coset.[6]
▶️Answer/Explanation
Markscheme
\(f(g) = f({e_G}g) = f({e_G})f(g)\) for \(g \in G\) M1A1
\( \Rightarrow f({e_G}) = {e_H}\) AG
[2 marks]
(i) closure: let \({k_1}\) and \({k_2} \in K\), then \(f({k_1}{k_2}) = f({k_1})f({k_2})\) M1A1
\( = {e_H}{e_H} = {e_H}\) A1
hence \({k_1}{k_2} \in K\) R1
(ii) K is non-empty because \({e_G}\) belongs to K R1
a closed non-empty subset of a finite group is a subgroup R1AG
[6 marks]
(i) \(f(gk{g^{ – 1}}) = f(g)f(k)f({g^{ – 1}})\) M1
\( = f(g){e_H}f({g^{ – 1}}) = f(g{g^{ – 1}})\) A1
\( = f({e_G}) = {e_H}\) A1
\( \Rightarrow gk{g^{ – 1}} \in K\) AG
(ii) clear definition of both left and right cosets, seen somewhere. A1
use of part (i) to show \(gK \subseteq Kg\) M1
similarly \(Kg \subseteq gK\) A1
hence \(gK = Kg\) AG
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
A group \(\{ D,{\text{ }}{ \times _3}\} \) is defined so that \(D = \{ 1,{\text{ }}2\} \) and \({ \times _3}\) is multiplication modulo \(3\).
A function \(f:\mathbb{Z} \to D\) is defined as \(f:x \mapsto \left\{ {\begin{array}{*{20}{c}} {1,{\text{ }}x{\text{ is even}}} \\ {2,{\text{ }}x{\text{ is odd}}} \end{array}} \right.\).
a.Prove that the function \(f\) is a homomorphism from the group \(\{ \mathbb{Z},{\text{ }} + \} {\text{ to }}\{ D,{\text{ }}{ \times _3}\} \).[6]
b.Find the kernel of \(f\).[3]
c.Prove that \(\{ {\text{Ker}}(f),{\text{ }} + \} \) is a subgroup of \(\{ \mathbb{Z},{\text{ }} + \} \).[4]
▶️Answer/Explanation
Markscheme
consider the cases, \(a\) and \(b\) both even, one is even and one is odd and \(a\) and \(b\) are both odd (M1)
calculating \(f(a + b)\) and \(f(a){ \times _3}f(b)\) in at least one case M1
if \(a\) is even and \(b\) is even, then \(a + b\) is even
so\(\;\;\;f(a + b) = 1.\;\;\;f(a){ \times _3}f(b) = 1{ \times _3}1 = 1\) A1
so\(\;\;\;f(a + b) = f(a){ \times _3}f(b)\)
if one is even and the other is odd, then \(a + b\) is odd
so\(\;\;\;f(a + b) = 2.\;\;\;f(a){ \times _3}f(b) = 1{ \times _3}2 = 2\) A1
so\(\;\;\;f(a + b) = f(a){ \times _3}f(b)\)
if \(a\) is odd and \(b\) is odd, then \(a + b\) is even
so\(\;\;\;f(a + b) = 1.\;\;\;f(a){ \times _3}f(b) = 2{ \times _3}2 = 1\) A1
so\(\;\;\;f(a + b) = f(a){ \times _3}f(b)\)
as\(\;\;\;f(a + b) = f(a){ \times _3}f(b)\;\;\;\)in all cases, so\(\;\;\;f:\mathbb{Z} \to D\) is a homomorphism R1AG
[6 marks]
\(1\) is the identity of \(\{ D,{\text{ }}{ \times _3}\} \) (M1)(A1)
so\(\;\;\;{\text{Ker}}(f)\) is all even numbers A1
[3 marks]
METHOD 1
sum of any two even numbers is even so closure applies A1
associative as it is a subset of \(\{ \mathbb{Z},{\text{ }} + \} \) A1
identity is \(0\), which is in the kernel A1
the inverse of any even number is also even A1
METHOD 2
\({\text{ker}}(f) \ne \emptyset \)
\({b^{ – 1}} \in {\text{ker}}(f)\) for any \(b\)
\(a{b^{ – 1}} \in {\text{ker}}(f)\) for any \(a\) and \(b\)
Note: Allow a general proof that the Kernel is always a subgroup.
[4 marks]
Total [13 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
The group \(\{ G,{\text{ }} * \} \) is Abelian and the bijection \(f:{\text{ }}G \to G\) is defined by \(f(x) = {x^{ – 1}},{\text{ }}x \in G\).
Show that \(f\) is an isomorphism.
▶️Answer/Explanation
Markscheme
we need to show that \(f(a * b) = f(a) * f(b)\) R1
Note: This R1 may be awarded at any stage.
let \(a,{\text{ }}b \in G\) (M1)
consider \(f(a) * f(b)\) M1
\( = {a^{ – 1}} * {b^{ – 1}}\) A1
consider \(f(a * b) = {(a * b)^{ – 1}}\) M1
\( = {b^{ – 1}} * {a^{ – 1}}\) A1
\( = {a^{ – 1}} * {b^{ – 1}}\) since \(G\) is Abelian R1
hence \(f\) is an isomorphism AG
[7 marks]
Examiners report
A surprising number of candidates wasted time and unrewarded effort showing that the mapping \(f\), stated to be a bijection in the question, actually was a bijection. Many candidates failed to get full marks by not properly using the fact that the group was stated to be Abelian. There were also candidates who drew the graph of \(y = \frac{1}{x}\) or otherwise assumed that the inverse of \(x\) was its reciprocal – this is unacceptable in the context of an abstract group question.
Question
The groups \(\{ K,{\text{ }} * \} \) and \(\{ H,{\text{ }} \odot \} \) are defined by the following Cayley tables.
G 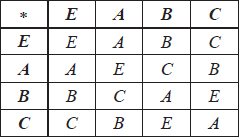
H 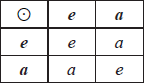
By considering a suitable function from G to H , show that a surjective homomorphism exists between these two groups. State the kernel of this homomorphism.
▶️Answer/Explanation
Markscheme
consider the function f given by
\(f(E) = e\)
\(f(A) = e\)
\(f(B) = a\) M1A1
\(f(C) = a\)
then, it has to be shown that
\(f(X * Y) = f(X) \odot f(Y){\text{ for all }}X{\text{ , }}Y \in G\) (M1)
consider
\(f\left( {(E{\text{ or }}A) * (E{\text{ or }}A)} \right) = f(E{\text{ or }}A) = e;{\text{ }}f(E{\text{ or }}A) \odot f(E{\text{ or }}A) = e \odot e = e\) M1A1
\(f\left( {(E{\text{ or }}A) * (B{\text{ or }}C)} \right) = f(B{\text{ or }}C) = a;{\text{ }}f(E{\text{ or }}A) \odot f(B{\text{ or }}C) = e \odot a = a\) A1
\(f\left( {(B{\text{ or }}C) * (B{\text{ or }}C)} \right) = f(E{\text{ or }}A) = e;{\text{ }}f(B{\text{ or }}C) \odot f(B{\text{ or }}C) = a \odot a = e\) A1
since the groups are Abelian, there is no need to consider \(f\left( {(B{\text{ or }}C) * (E{\text{ or }}A)} \right)\) R1
the required property is satisfied in all cases so the homomorphism exists
Note: A comprehensive proof using tables is acceptable.
the kernel is \(\{ E,{\text{ }}A\} \) A1
[9 marks]
