Question
(a) Find the six roots of the equation \({z^6} – 1 = 0\) , giving your answers in the form \(r\,{\text{cis}}\,\theta {\text{, }}r \in {\mathbb{R}^ + }{\text{, }}0 \leqslant \theta < 2\pi \) .
(b) (i) Show that these six roots form a group G under multiplication of complex numbers.
(ii) Show that G is cyclic and find all the generators.
(iii) Give an example of another group that is isomorphic to G, stating clearly the corresponding elements in the two groups.
▶️Answer/Explanation
Markscheme
(a) \({z^6} = 1 = {\text{cis}}\,2n\pi \) (M1)
The six roots are
\({\text{cis}}\,0(1),{\text{ cis}}\frac{\pi }{3},{\text{ cis}}\frac{{2\pi }}{3},{\text{ cis}}\,\pi ( – 1),{\text{ cis}}\frac{{4\pi }}{3},{\text{ cis}}\frac{{5\pi }}{3}\) A3
Note: Award A2 for 4 or 5 correct roots, A1 for 2 or 3 correct roots.
[4 marks]
(b) (i) Closure: Consider any two roots \({\text{cis}}\frac{{m\pi }}{3},{\text{ cis}}\frac{{n\pi }}{3}\). M1
\({\text{cis}}\frac{{m\pi }}{3} \times {\text{cis}}\frac{{n\pi }}{3} = {\text{cis}}\,(m + n){\text{(mod6)}}\frac{\pi }{3} \in G\) A1
Note: Award M1A1 for a correct Cayley table showing closure.
Identity: The identity is 1. A1
Inverse: The inverse of \({\text{cis}}\frac{{m\pi }}{3}{\text{ is cis}}\frac{{(6 – m)\pi }}{3} \in G\) . A2
Associative: This follows from the associativity of multiplication. R1
The 4 group axioms are satisfied. R1
(ii) Successive powers of \({\text{cis}}\frac{\pi }{3}\left( {{\text{or cis}}\frac{{5\pi }}{3}} \right)\)
generate the group which is therefore cyclic. R2
The (only) other generator is \({\text{cis}}\frac{{5\pi }}{3}\left( {{\text{or cis}}\frac{\pi }{3}} \right)\) . A1
Note: Award A0 for any additional answers.
(iii) The group of the integers 0, 1, 2, 3, 4, 5 under addition modulo 6. R2
The correspondence is
\(m \to {\text{cis}}\frac{{m\pi }}{3}\) R1
Note: Accept any other cyclic group of order 6.
[13 marks]
Total [17 marks]
Examiners report
This question was reasonably well answered by many candidates, although in (b)(iii), some candidates were unable to give another group isomorphic to G.
Question
(a) Consider the set A = {1, 3, 5, 7} under the binary operation \( * \), where \( * \) denotes multiplication modulo 8.
(i) Write down the Cayley table for \(\{ A,{\text{ }} * \} \).
(ii) Show that \(\{ A,{\text{ }} * \} \) is a group.
(iii) Find all solutions to the equation \(3 * x * 7 = y\). Give your answers in the form \((x,{\text{ }}y)\).
(b) Now consider the set B = {1, 3, 5, 7, 9} under the binary operation \( \otimes \), where \( \otimes \) denotes multiplication modulo 10. Show that \(\{ B,{\text{ }} \otimes \} \) is not a group.
(c) Another set C can be formed by removing an element from B so that \(\{ C,{\text{ }} \otimes \} \) is a group.
(i) State which element has to be removed.
(ii) Determine whether or not \(\{ A,{\text{ }} * \} \) and \(\{ C,{\text{ }} \otimes \} \) are isomorphic.
▶️Answer/Explanation
Markscheme
(a) (i) 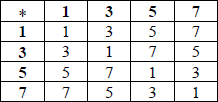 A3
A3
Note: Award A2 for 15 correct, A1 for 14 correct and A0 otherwise.
(ii) it is a group because:
the table shows closure A1
multiplication is associative A1
it possesses an identity 1 A1
justifying that every element has an inverse e.g. all self-inverse A1
(iii) (since \( * \) is commutative, \(5 * x = y\))
so solutions are (1, 5), (3, 7), (5, 1), (7, 3) A2
Notes: Award A1 for 3 correct and A0 otherwise.
Do not penalize extra incorrect solutions.
[9 marks]
(b) 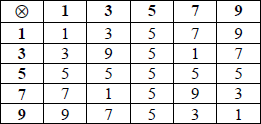
Note: It is not necessary to see the Cayley table.
a valid reason R2
e.g. from the Cayley table the 5 row does not give a Latin square, or 5 does not have an inverse, so it cannot be a group
[2 marks]
(c) (i) remove the 5 A1
(ii) they are not isomorphic because all elements in A are self-inverse this is not the case in C, (e.g. \(3 \otimes 3 = 9 \ne 1\)) R2
Note: Accept any valid reason.
[3 marks]
Total [14 marks]
Examiners report
Candidates are generally confident when dealing with a specific group and that was the situation again this year. Some candidates lost marks in (a)(ii) by not giving an adequate explanation for the truth of some of the group axioms, eg some wrote ‘every element has an inverse’. Since the question told the candidates that \(\{ A,{\text{ }} * )\) was a group, this had to be the case and the candidates were expected to justify their statement by noting that every element was self-inverse. Solutions to (c)(ii) were reasonably good in general, certainly better than solutions to questions involving isomorphisms set in previous years.
Question
Set \(S = \{ {x_0},{\text{ }}{x_1},{\text{ }}{x_2},{\text{ }}{x_3},{\text{ }}{x_4},{\text{ }}{x_5}\} \) and a binary operation \( \circ \) on S is defined as \({x_i} \circ {x_j} = {x_k}\), where \(i + j \equiv k(\bmod 6)\).
(a) (i) Construct the Cayley table for \(\{ S,{\text{ }} \circ \} \) and hence show that it is a group.
(ii) Show that \(\{ S,{\text{ }} \circ \} \) is cyclic.
(b) Let \(\{ G,{\text{ }} * \} \) be an Abelian group of order 6. The element \(a \in {\text{G}}\) has order 2 and the element \(b \in {\text{G}}\) has order 3.
(i) Write down the six elements of \(\{ G,{\text{ }} * \} \).
(ii) Find the order of \({\text{a}} * b\) and hence show that \(\{ G,{\text{ }} * \} \) is isomorphic to \(\{ S,{\text{ }} \circ \} \).
▶️/Explanation
Markscheme
(a) (i) Cayley table for \(\{ S,{\text{ }} \circ \} \)
\(\begin{array}{*{20}{c|cccccc}}
\circ &{{x_0}}&{{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}} \\
\hline
{{x_0}}&{{x_0}}&{{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}} \\
{{x_1}}&{{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}}&{{x_0}} \\
{{x_2}}&{{x_2}}&{{x_3}}&{{x_4}}&{{x_5}}&{{x_0}}&{{x_1}} \\
{{x_3}}&{{x_3}}&{{x_4}}&{{x_5}}&{{x_0}}&{{x_1}}&{{x_2}} \\
{{x_4}}&{{x_4}}&{{x_5}}&{{x_0}}&{{x_1}}&{{x_2}}&{{x_3}} \\
{{x_5}}&{{x_5}}&{{x_0}}&{{x_1}}&{{x_2}}&{{x_3}}&{{x_4}}
\end{array}\) A4
Note: Award A4 for no errors, A3 for one error, A2 for two errors, A1 for three errors and A0 for four or more errors.
S is closed under \( \circ \) A1
\({x_0}\) is the identity A1
\({x_0}\) and \({x_3}\) are self-inverses, A1
\({x_2}\) and \({x_4}\) are mutual inverses and so are \({x_1}\) and \({x_5}\) A1
modular addition is associative A1
hence, \(\{ S,{\text{ }} \circ \} \) is a group AG
(ii) the order of \({x_1}\) (or \({x_5}\)) is 6, hence there exists a generator, and \(\{ S,{\text{ }} \circ \} \) is a cyclic group A1R1
[11 marks]
(b) (i) e, a, b, ab A1
and \({b^2},{\text{ }}a{b^2}\) A1A1
Note: Accept \(ba\) and \({b^2}a\).
(ii) \({(ab)^2} = {b^2}\) M1A1
\({(ab)^3} = a\) A1
\({(ab)^4} = b\) A1
hence order is 6 A1
groups G and S have the same orders and both are cyclic R1
hence isomorphic AG
[9 marks]
Total [20 marks]
Examiners report
a) Most candidates had the correct Cayley table and were able to show successfully that the group axioms were satisfied. Some candidates, however, simply stated that an inverse exists for each element without stating the elements and their inverses. Most candidates were able to find a generator and hence show that the group is cyclic.
b) This part was answered less successfully by many candidates. Some failed to find all the elements. Some stated that the order of ab is 6 without showing any working.
Question
a.Given that p , q and r are elements of a group, prove the left-cancellation rule, i.e. \(pq = pr \Rightarrow q = r\) .
Your solution should indicate which group axiom is used at each stage of the proof.[4]
b.Consider the group G , of order 4, which has distinct elements a , b and c and the identity element e .
(i) Giving a reason in each case, explain why ab cannot equal a or b .
(ii) Given that c is self inverse, determine the two possible Cayley tables for G .
(iii) Determine which one of the groups defined by your two Cayley tables is isomorphic to the group defined by the set {1, −1, i, −i} under multiplication of complex numbers. Your solution should include a correspondence between a, b, c, e and 1, −1, i, −i .[10]
▶️Answer/Explanation
Markscheme
\(pq = pr\)
\({p^{ – 1}}(pq) = {p^{ – 1}}(pr)\) , every element has an inverse A1
\(({p^{ – 1}}p)q = ({p^{ – 1}}p)r\) , Associativity A1
Note: Brackets in lines 2 and 3 must be seen.
\(eq = er\), \({p^{ – 1}}p = e\), the identity A1
\(q = r\), \(ea = a\) for all elements a of the group A1
[4 marks]
(i) let ab = a so b = e be which is a contradiction R1
let ab = b so a = e which is a contradiction R1
therefore ab cannot equal either a or b AG
(ii) the two possible Cayley tables are
table 1
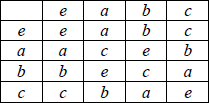 A2
A2
table 2
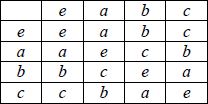 A2
A2
(iii) the group defined by table 1 is isomorphic to the given group R1
because
EITHER
both contain one self-inverse element (other than the identity) R1
OR
both contain an inverse pair R1
OR
both are cyclic R1
THEN
the correspondence is \(e \to 1\), \(c \to – 1\), \(a \to i\), \(b \to – i\)
(or vice versa for the last two) A2
Note: Award the final A2 only if the correct group table has been identified.
[10 marks]
Examiners report
Solutions to (a) were often poor with inadequate explanations often seen. It was not uncommon to see \(pq = pr\)
\({p^{ – 1}}pq = {p^{ – 1}}pr\)
\(q = r\)
without any mention of associativity. Many candidates understood what was required in (b)(i), but solutions to (b)(ii) were often poor with the tables containing elements such as ab and bc without simplification. In (b)(iii), candidates were expected to determine the isomorphism by noting that the group defined by {1, –1, i, –i} under multiplication is cyclic or that –1 is the only self-inverse element apart from the identity, without necessarily writing down the Cayley table in full which many candidates did. Many candidates just stated that there was a bijection between the two groups without giving any justification for this.
Solutions to (a) were often poor with inadequate explanations often seen. It was not uncommon to see \(pq = pr\)
\({p^{ – 1}}pq = {p^{ – 1}}pr\)
\(q = r\)
without any mention of associativity. Many candidates understood what was required in (b)(i), but solutions to (b)(ii) were often poor with the tables containing elements such as ab and bc without simplification. In (b)(iii), candidates were expected to determine the isomorphism by noting that the group defined by {1, –1, i, –i} under multiplication is cyclic or that –1 is the only self-inverse element apart from the identity, without necessarily writing down the Cayley table in full which many candidates did. Many candidates just stated that there was a bijection between the two groups without giving any justification for this.
Question
The group \(\{ G,{\text{ }} * \} \) is Abelian and the bijection \(f:{\text{ }}G \to G\) is defined by \(f(x) = {x^{ – 1}},{\text{ }}x \in G\).
Show that \(f\) is an isomorphism.
▶️Answer/Explanation
Markscheme
we need to show that \(f(a * b) = f(a) * f(b)\) R1
Note: This R1 may be awarded at any stage.
let \(a,{\text{ }}b \in G\) (M1)
consider \(f(a) * f(b)\) M1
\( = {a^{ – 1}} * {b^{ – 1}}\) A1
consider \(f(a * b) = {(a * b)^{ – 1}}\) M1
\( = {b^{ – 1}} * {a^{ – 1}}\) A1
\( = {a^{ – 1}} * {b^{ – 1}}\) since \(G\) is Abelian R1
hence \(f\) is an isomorphism AG
[7 marks]
Examiners report
A surprising number of candidates wasted time and unrewarded effort showing that the mapping \(f\), stated to be a bijection in the question, actually was a bijection. Many candidates failed to get full marks by not properly using the fact that the group was stated to be Abelian. There were also candidates who drew the graph of \(y = \frac{1}{x}\) or otherwise assumed that the inverse of \(x\) was its reciprocal – this is unacceptable in the context of an abstract group question.
