IB DP Maths Topic 8.6 Proof that left-cancellation and right-cancellation by an element a hold, provided that a has an inverse. HL Paper 3

\(pq = pr\)

\({p^{ – 1}}(pq) = {p^{ – 1}}(pr)\) , every element has an inverse     A1

\(({p^{ – 1}}p)q = ({p^{ – 1}}p)r\) , Associativity     A1

Note: Brackets in lines 2 and 3 must be seen.

\(eq = er\), \({p^{ – 1}}p = e\), the identity     A1

\(q = r\), \(ea = a\) for all elements a of the group     A1

[4 marks]

(i)     let ab = a so b = e be which is a contradiction     R1

let ab = b so a = e which is a contradiction     R1

therefore ab cannot equal either a or b     AG

(ii)     the two possible Cayley tables are

table 1

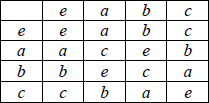     A2

table 2

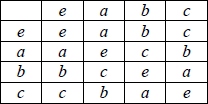     A2

(iii)     the group defined by table 1 is isomorphic to the given group     R1

because

EITHER

both contain one self-inverse element (other than the identity)     R1

OR

both contain an inverse pair     R1

OR

both are cyclic     R1

THEN

the correspondence is \(e \to 1\), \(c \to – 1\), \(a \to i\), \(b \to – i\)

(or vice versa for the last two)     A2

Note: Award the final A2 only if the correct group table has been identified.

[10 marks]

Solutions to (a) were often poor with inadequate explanations often seen. It was not uncommon to see \(pq = pr\)

\({p^{ – 1}}pq = {p^{ – 1}}pr\)

\(q = r\)

without any mention of associativity. Many candidates understood what was required in (b)(i), but solutions to (b)(ii) were often poor with the tables containing elements such as ab and bc without simplification. In (b)(iii), candidates were expected to determine the isomorphism by noting that the group defined by {1, –1, i, –i} under multiplication is cyclic or that –1 is the only self-inverse element apart from the identity, without necessarily writing down the Cayley table in full which many candidates did. Many candidates just stated that there was a bijection between the two groups without giving any justification for this.

Solutions to (a) were often poor with inadequate explanations often seen. It was not uncommon to see \(pq = pr\)

\({p^{ – 1}}pq = {p^{ – 1}}pr\)

\(q = r\)

without any mention of associativity. Many candidates understood what was required in (b)(i), but solutions to (b)(ii) were often poor with the tables containing elements such as ab and bc without simplification. In (b)(iii), candidates were expected to determine the isomorphism by noting that the group defined by {1, –1, i, –i} under multiplication is cyclic or that –1 is the only self-inverse element apart from the identity, without necessarily writing down the Cayley table in full which many candidates did. Many candidates just stated that there was a bijection between the two groups without giving any justification for this.