Question
(a) Draw the Cayley table for the set of integers G = {0, 1, 2, 3, 4, 5} under addition modulo 6, \({ + _6}\).
(b) Show that \(\{ G,{\text{ }}{ + _6}\} \) is a group.
(c) Find the order of each element.
(d) Show that \(\{ G,{\text{ }}{ + _6}\} \) is cyclic and state its generators.
(e) Find a subgroup with three elements.
(f) Find the other proper subgroups of \(\{ G,{\text{ }}{ + _6}\} \).
▶️Answer/Explanation
Markscheme
(a) 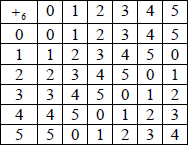 A3
A3
Note: Award A2 for 1 error, A1 for 2 errors and A0 for more than 2 errors.
[3 marks]
(b) The table is closed A1
Identity element is 0 A1
Each element has a unique inverse (0 appears exactly once in each row and column) A1
Addition mod 6 is associative A1
Hence \(\{ G,{\text{ }}{ + _6}\} \) forms a group AG
[4 marks]
(c) 0 has order 1 (0 = 0),
1 has order 6 (1 + 1 + 1 + 1 + 1 + 1 = 0),
2 has order 3 (2 + 2 + 2 = 0),
3 has order 2 (3 + 3 = 0),
4 has order 3 (4 + 4 + 4 = 0),
5 has order 6 (5 + 5 + 5 + 5 + 5 + 5 = 0). A3
Note: Award A2 for 1 error, A1 for 2 errors and A0 for more than 2 errors.
[3 marks]
(d) Since 1 and 5 are of order 6 (the same as the order of the group) every element can be written as sums of either 1 or 5. Hence the group is cyclic. R1
The generators are 1 and 5. A1
[2 marks]
(e) A subgroup of order 3 is \(\left( {\{ 0,{\text{ }}2,{\text{ }}4\} ,{\text{ }}{ + _6}} \right)\) A2
Note: Award A1 if only {0, 2, 4} is seen.
[2 marks]
(f) Other proper subgroups are \(\left( {\{ 0\} { + _6}} \right),{\text{ }}\left( {\{ 0,{\text{ }}3\} { + _6}} \right)\) A1A1
Note: Award A1 if only {0}, {0, 3} is seen.
[2 marks]
Total [16 marks]
Examiners report
The table was well done as was showing its group properties. The order of the elements in (b) was done well except for the order of 0 which was often not given. Finding the generators did not seem difficult but correctly stating the subgroups was not often done. The notion of a ‘proper’ subgroup is not well known.
Question
The group G has a subgroup H. The relation R is defined on G by xRy if and only if \(x{y^{ – 1}} \in H\), for \(x,{\text{ }}y \in G\).
a.Show that R is an equivalence relation.[8]
b.The Cayley table for G is shown below.
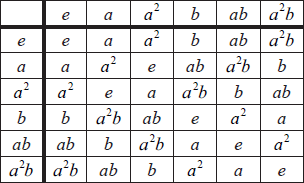
The subgroup H is given as \(H = \{ e,{\text{ }}{a^2}b\} \).
(i) Find the equivalence class with respect to R which contains ab.
(ii) Another equivalence relation \(\rho \) is defined on G by \(x\rho y\) if and only if \({x^{ – 1}}y \in H\), for \(x,{\text{ }}y \in G\). Find the equivalence class with respect to \(\rho \) which contains ab.[6]
▶️Answer/Explanation
Markscheme
\(x{x^{ – 1}} = e \in H\) M1
\( \Rightarrow xRx\)
hence R is reflexive A1
if xRy then \(x{y^{ – 1}} \in H\)
\( \Rightarrow {(x{y^{ – 1}})^{ – 1}} \in H\) M1
now \((x{y^{ – 1}}){(x{y^{ – 1}})^{ – 1}} = e\) and \(x{y^{ – 1}}y{x^{ – 1}} = e\)
\( \Rightarrow {(x{y^{ – 1}})^{ – 1}} = y{x^{ – 1}}\) A1
hence \(y{x^{ – 1}} \in H \Rightarrow yRx\)
hence R is symmetric A1
if xRy, yRz then \(x{y^{ – 1}} \in H,{\text{ }}y{z^{ – 1}} \in H\) M1
\( \Rightarrow (x{y^{ – 1}})(y{z^{ – 1}}) \in H\) M1
\( \Rightarrow x({y^{ – 1}}y){z^{ – 1}} \in H\)
\( \Rightarrow {x^{ – 1}}z \in H\)
hence R is transitive A1
hence R is an equivalence relation AG
[8 marks]
(i) for the equivalence class, solving:
EITHER
\(x{(ab)^{ – 1}} = e{\text{ or }}x{(ab)^{ – 1}} = {a^2}b\) (M1)
\(\{ ab,{\text{ }}a\} \) A2
OR
\(ab{(x)^{ – 1}} = e{\text{ or }}ab{(x)^{ – 1}} = {a^2}b\) (M1)
\(\{ ab,{\text{ }}a\} \) A2
(ii) for the equivalence class, solving:
EITHER
\({x^{ – 1}}(ab) = e{\text{ or }}{x^{ – 1}}(ab) = {a^2}b\) (M1)
\(\{ ab,{\text{ }}{a^2}\} \) A2
OR
\({(ab)^{ – 1}}x = e{\text{ or }}{(ab)^{ – 1}}x = {a^2}b\) (M1)
\(\{ ab,{\text{ }}{a^2}\} \) A2
[6 marks]
Examiners report
Stronger candidates made a reasonable start to (a), and many were able to demonstrate that the relation was reflexive and transitive. However, the majority of candidates struggled to make a meaningful attempt to show the relation was symmetric, with many making unfounded assumptions. Equivalence classes still cause major problems and few fully correct answers were seen to (b).
Stronger candidates made a reasonable start to (a), and many were able to demonstrate that the relation was reflexive and transitive. However, the majority of candidates struggled to make a meaningful attempt to show the relation was symmetric, with many making unfounded assumptions. Equivalence classes still cause major problems and few fully correct answers were seen to (b).
Question
a.Associativity and commutativity are two of the five conditions for a set S with the binary operation \( * \) to be an Abelian group; state the other three conditions.[2]
b.The Cayley table for the binary operation \( \odot \) defined on the set T = {p, q, r, s, t} is given below.

(i) Show that exactly three of the conditions for {T , \( \odot \)} to be an Abelian group are satisfied, but that neither associativity nor commutativity are satisfied.
(ii) Find the proper subsets of T that are groups of order 2, and comment on your result in the context of Lagrange’s theorem.
(iii) Find the solutions of the equation \((p \odot x) \odot x = x \odot p\) .[15]
▶️Answer/Explanation
Markscheme
closure, identity, inverse A2
Note: Award A1 for two correct properties, A0 otherwise.
[2 marks]
(i) closure: there are no extra elements in the table R1
identity: s is a (left and right) identity R1
inverses: all elements are self-inverse R1
commutative: no, because the table is not symmetrical about the leading diagonal, or by counterexample R1
associativity: for example, \((pq)t = rt = p\) M1A1
not associative because \(p(qt) = pr = t \ne p\) R1
Note: Award M1A1 for 1 complete example whether or not it shows non-associativity.
(ii) \(\{ s,\,p\} ,{\text{ }}\{ s,\,q\} ,{\text{ }}\{ s,\,r\} ,{\text{ }}\{ s,\,t\} \) A2
Note: Award A1 for 2 or 3 correct sets.
as 2 does not divide 5, Lagrange’s theorem would have been contradicted if T had been a group R1
(iii) any attempt at trying values (M1)
the solutions are q, r, s and t A1A1A1A1
Note: Deduct A1 if p is included.
[15 marks]
Examiners report
This was on the whole a well answered question and it was rare for a candidate not to obtain full marks on part (a). In part (b) the vast majority of candidates were able to show that the set satisfied the properties of a group apart from associativity which they were also familiar with. Virtually all candidates knew the difference between commutativity and associativity and were able to distinguish between the two. Candidates were familiar with Lagrange’s Theorem and many were able to see how it did not apply in the case of this problem. Many candidates found a solution method to part (iii) of the problem and obtained full marks.
This was on the whole a well answered question and it was rare for a candidate not to obtain full marks on part (a). In part (b) the vast majority of candidates were able to show that the set satisfied the properties of a group apart from associativity which they were also familiar with. Virtually all candidates knew the difference between commutativity and associativity and were able to distinguish between the two. Candidates were familiar with Lagrange’s Theorem and many were able to see how it did not apply in the case of this problem. Many candidates found a solution method to part (iii) of the problem and obtained full marks.
Question
Consider the set S defined by \(S = \{ s \in \mathbb{Q}:2s \in \mathbb{Z}\} \).
You may assume that \( + \) (addition) and \( \times \) (multiplication) are associative binary operations
on \(\mathbb{Q}\).
a.(i) Write down the six smallest non-negative elements of \(S\).
(ii) Show that \(\{ S,{\text{ }} + \} \) is a group.
(iii) Give a reason why \(\{ S,{\text{ }} \times \} \) is not a group. Justify your answer.[9]
b.The relation \(R\) is defined on \(S\) by \({s_1}R{s_2}\) if \(3{s_1} + 5{s_2} \in \mathbb{Z}\).
(i) Show that \(R\) is an equivalence relation.
(ii) Determine the equivalence classes.[10]
▶️Answer/Explanation
Markscheme
(i) \({\text{0, }}\frac{{\text{1}}}{{\text{2}}}{\text{, 1, }}\frac{{\text{3}}}{{\text{2}}}{\text{, 2, }}\frac{{\text{5}}}{{\text{2}}}\) A2
Notes: A2 for all correct, A1 for three to five correct.
(ii) EITHER
closure: if \({s_1},{\text{ }}{s_2} \in S\), then \({s_1} = \frac{m}{2}\) and \({s_2} = \frac{n}{2}\) for some \(m,{\text{ }}n \in {\text{¢}}\). M1
Note: Accept two distinct examples (eg, \(\frac{1}{2} + \frac{1}{2} = 1;{\text{ }}\frac{1}{2} + 1 = \frac{3}{2}\)) for the M1.
\({s_1} + {s_2} = \frac{{m + n}}{2} \in S\) A1
OR
the sum of two half-integers A1
is a half-integer R1
THEN
identity: 0 is the (additive) identity A1
inverse: \(s + ( – s) = 0\), where \( – s \in S\) A1
it is associative (since \(S \subset \S\)) A1
the group axioms are satisfied AG
(iii) EITHER
the set is not closed under multiplication, A1
for example, \(\frac{1}{2} \times \frac{1}{2} = \frac{1}{4}\), but \(\frac{1}{4} \notin S\) R1
OR
not every element has an inverse, A1
for example, 3 does not have an inverse R1
[9 marks]
(i) reflexive: consider \(3s + 5s\) M1
\( = 8s \in {\text{¢}} \Rightarrow \) reflexive A1
symmetric: if \({s_1}R{s_2}\), consider \(3{s_2} + 5{s_1}\) M1
for example, \( = 3{s_1} + 5{s_2} + (2{s_1} – 2{s_2}) \in {\text{¢}} \Rightarrow \)symmetric A1
transitive: if \({s_1}R{s_2}\) and \({s_2}R{s_3}\), consider (M1)
\(3{s_1} + 5{s_3} = (3{s_1} + 5{s_2}) + (3{s_2} + 5{s_3}) – 8{s_2}\) M1
\( \in {\text{¢}} \Rightarrow \)transitive A1
so R is an equivalence relation AG
(ii) \({C_1} = {\text{¢}}\) A1
\({C_2} = \left\{ { \pm \frac{1}{2},{\text{ }} \pm \frac{3}{2},{\text{ }} \pm \frac{5}{2},{\text{ }} \ldots } \right\}\) A1A1
Note: A1 for half odd integers and A1 for ±.
[10 marks]
Examiners report
[N/A]
[N/A]
Question
The binary operation \( * \) is defined on the set \(T = \{ 0,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6\} \) by \(a * b = (a + b – ab)(\bmod 7),{\text{ }}a,{\text{ }}b \in T\).
a.Copy and complete the following Cayley table for \(\{ T,{\text{ }} * \} \).
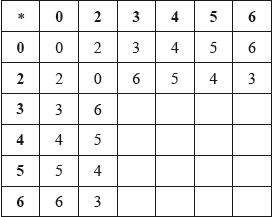 [4]
[4]
b.Prove that \(\{ T,{\text{ }} * \} \) forms an Abelian group.[7]
c.Find the order of each element in \(T\).[4]
d.Given that \(\{ H,{\text{ }} * \} \) is the subgroup of \(\{ T,{\text{ }} * \} \) of order \(2\), partition \(T\) into the left cosets with respect to \(H\).[3]
▶️Answer/Explanation
Markscheme
Cayley table is
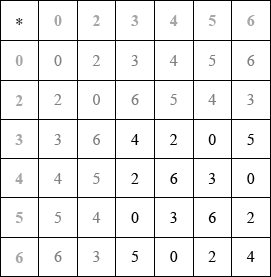 A4
A4
award A4 for all 16 correct, A3 for up to 2 errors, A2 for up to 4 errors, A1 for up to 6 errors
[4 marks]
closed as no other element appears in the Cayley table A1
symmetrical about the leading diagonal so commutative R1
hence it is Abelian
\(0\) is the identity
as \(x * 0( = 0 * x) = x + 0 – 0 = x\) A1
\(0\) and \(2\) are self inverse, \(3\) and \(5\) is an inverse pair, \(4\) and \(6\) is an inverse pair A1
Note: Accept “Every row and every column has a \(0\) so each element has an inverse”.
\((a * b) * c = (a + b – ab) * c = a + b – ab + c – (a + b – ab)c\) M1
\( = a + b + c – ab – ac – bc + abc\) A1
\(a * (b * c) = a * (b + c – bc) = a + b + c – bc – a(b + c – bc)\) A1
\( = a + b + c – ab – ac – bc + abc\)
so \((a * b) * c = a * (b * c)\) and \( * \) is associative
Note: Inclusion of mod 7 may be included at any stage.
[7 marks]
\(0\) has order \(1\) and \(2\) has order \(2\) A1
\({3^2} = 4,{\text{ }}{3^3} = 2,{\text{ }}{3^4} = 6,{\text{ }}{3^5} = 5,{\text{ }}{3^6} = 0\) so \(3\) has order \(6\) A1
\({4^2} = 6,{\text{ }}{4^3} = 0\) so \(4\) has order \(3\) A1
\(5\) has order \(6\) and \(6\) has order \(3\) A1
[4 marks]
\(H = \{ 0,{\text{ }}2\} \) A1
\(0 * \{ 0,{\text{ }}2\} = \{ 0,{\text{ }}2\} ,{\text{ }}2 * \{ 0,{\text{ }}2\} = \{ 2,{\text{ }}0\} ,{\text{ }}3 * \{ 0,{\text{ }}2\} = \{ 3,{\text{ }}6\} ,{\text{ }}4 * \{ 0,{\text{ }}2\} = \{ 4,{\text{ }}5\} ,\)
\(5 * \{ 0,{\text{ }}2\} = \{ 5,{\text{ }}4\} ,{\text{ }}6 * \{ 0,{\text{ }}2\} = \{ 6,{\text{ }}3\} \) M1
Note: Award the M1 if sufficient examples are used to find at least two of the cosets.
so the left cosets are \(\{ 0,{\text{ }}2\} ,{\text{ }}\{ 3,{\text{ }}6\} ,{\text{ }}\{ 4,{\text{ }}5\} \) A1
[3 marks]
Total [18 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
The following Cayley table for the binary operation multiplication modulo 9, denoted by \( * \), is defined on the set \(S = \{ 1,{\text{ }}2,{\text{ }}4,{\text{ }}5,{\text{ }}7,{\text{ }}8\} \).
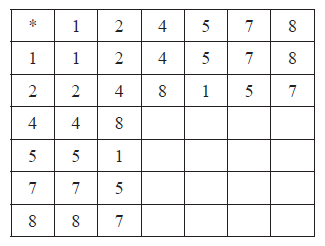
a.Copy and complete the table.[3]
b.Show that \(\{ S,{\text{ }} * \} \) is an Abelian group.[5]
c.Determine the orders of all the elements of \(\{ S,{\text{ }} * \} \).[3]
d.(i) Find the two proper subgroups of \(\{ S,{\text{ }} * \} \).
(ii) Find the coset of each of these subgroups with respect to the element 5.[4]
e.Solve the equation \(2 * x * 4 * x * 4 = 2\).[4]
▶️Answer/Explanation
Markscheme
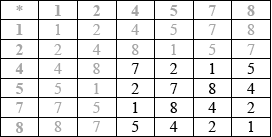 A3
A3
Note: Award A3 for correct table, A2 for one or two errors, A1 for three or four errors and A0 otherwise.
[3 marks]
the table contains only elements of \(S\), showing closure R1
the identity is 1 A1
every element has an inverse since 1 appears in every row and column, or a complete list of elements and their correct inverses A1
multiplication of numbers is associative A1
the four axioms are satisfied therefore \(\{ S,{\text{ }} * \} \) is a group
the group is Abelian because the table is symmetric (about the leading diagonal) A1
[5 marks]
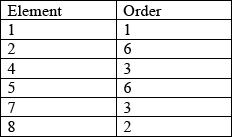 A3
A3
Note: Award A3 for all correct values, A2 for 5 correct, A1 for 4 correct and A0 otherwise.
[3 marks]
(i) the subgroups are \(\{ 1,{\text{ }}8\} \); \(\{ 1,{\text{ }}4,{\text{ }}7\} \) A1A1
(ii) the cosets are \(\{ 4,{\text{ }}5\} \); \(\{ 2,{\text{ }}5,{\text{ }}8\} \) A1A1
[4 marks]
METHOD 1
use of algebraic manipulations M1
and at least one result from the table, used correctly A1
\(x = 2\) A1
\(x = 7\) A1
METHOD 2
testing at least one value in the equation M1
obtain \(x = 2\) A1
obtain \(x = 7\) A1
explicit rejection of all other values A1
[4 marks]
Examiners report
The majority of candidates were able to complete the Cayley table correctly.
Generally well done. However, it is not good enough for a candidate to say something along the lines of ‘the operation is closed or that inverses exist by looking at the Cayley table’. A few candidates thought they only had to prove commutativity.
Often well done. A few candidates stated extra, and therefore incorrect subgroups.
[N/A]
The majority found only one solution, usually the obvious \(x = 2\), but sometimes only the less obvious \(x = 7\).
