Question
Determine, giving reasons, which of the following sets form groups under the operations given below. Where appropriate you may assume that multiplication is associative.
(a) \(\mathbb{Z}\) under subtraction.
(b) The set of complex numbers of modulus 1 under multiplication.
(c) The set {1, 2, 4, 6, 8} under multiplication modulo 10.
(d) The set of rational numbers of the form
\[\frac{{3m + 1}}{{3n + 1}},{\text{ where }}m,{\text{ }}n \in \mathbb{Z}\]
under multiplication.
▶️Answer/Explanation
Markscheme
(a) not a group A1
EITHER
subtraction is not associative on \(\mathbb{Z}\) (or give counter-example) R1
OR
there is a right-identity, 0, but it is not a left-identity R1
[2 marks]
(b) the set forms a group A1
the closure is a consequence of the following relation (and the closure of \(\mathbb{C}\) itself):
\(\left| {{z_1}{z_2}} \right| = \left| {{z_1}} \right|\left| {{z_2}} \right|\) R1
the set contains the identity 1 R1
that inverses exist follows from the relation
\(\left| {{z^{ – 1}}} \right| = {\left| z \right|^{ – 1}}\)
for non-zero complex numbers R1
[4 marks]
(c) not a group A1
for example, only the identity element 1 has an inverse R1
[2 marks]
(d) the set forms a group A1
\(\frac{{2m + 1}}{{3n + 1}} \times \frac{{3s + 1}}{{3t + 1}} = \frac{{9ms + 3s + 3m + 1}}{{9nt + 3n + 3t + 1}} = \frac{{3(3ms + s + m) + 1}}{{3(3nt + n + t) + 1}}\) M1R1
shows closure
the identity 1 corresponds to m = n = 0 R1
an inverse corresponds to interchanging the parameters m and n R1
[5 marks]
Total [13 marks]
Examiners report
There was a mixed response to this question. Some candidates were completely out of their depth. Stronger candidates provided satisfactory answers to parts (a) and (c). For the other parts there was a general lack of appreciation that, for example, closure and the existence of inverses, requires that products and inverses have to be shown to be members of the set.
Question
The group \(\{ G,{\text{ }}{ \times _7}\} \) is defined on the set {1, 2, 3, 4, 5, 6} where \({ \times _7}\) denotes multiplication modulo 7.
a.(i) Write down the Cayley table for \(\{ G,{\text{ }}{ \times _7}\} \) .
(ii) Determine whether or not \(\{ G,{\text{ }}{ \times _7}\} \) is cyclic.
(iii) Find the subgroup of G of order 3, denoting it by H .
(iv) Identify the element of order 2 in G and find its coset with respect to H .[10]
(i) Show that \(\{ K,{\text{ }} \circ \} \) is non-Abelian.
(ii) Giving a reason, state whether or not \(\{ G,{\text{ }}{ \times _7}\} \) and \(\{ K,{\text{ }} \circ \} \) are isomorphic.[6]
▶️Answer/Explanation
Markscheme
(i) the Cayley table is
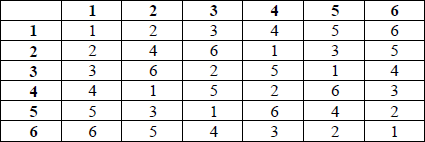 A3
A3
Note: Deduct 1 mark for each error up to a maximum of 3.
(ii) by considering powers of elements, (M1)
it follows that 3 (or 5) is of order 6 A1
so the group is cyclic A1
(iii) we see that 2 and 4 are of order 3 so the subgroup of order 3 is {1, 2, 4} M1A1
(iv) the element of order 2 is 6 A1
the coset is {3, 5, 6} A1
[10 marks]
(i) consider for example
\(\left( {\begin{array}{*{20}{c}}
1&2&3 \\
2&1&3
\end{array}} \right) \circ \left( {\begin{array}{*{20}{c}}
1&2&3 \\
2&3&1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1&2&3 \\
1&3&2
\end{array}} \right)\) M1A1
\(\left( {\begin{array}{*{20}{c}}
1&2&3 \\
2&3&1
\end{array}} \right) \circ \left( {\begin{array}{*{20}{c}}
1&2&3 \\
2&1&3
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1&2&3 \\
3&2&1
\end{array}} \right)\) M1A1
Note: Award M1A1M1A0 if both compositions are done in the wrong order.
Note: Award M1A1M0A0 if the two compositions give the same result, if no further attempt is made to find two permutations which are not commutative.
these are different so the group is not Abelian R1AG
(ii) they are not isomorphic because \(\{ G,{\text{ }}{ \times _7}\} \) is Abelian and \(\{ K,{\text{ }} \circ \} \) is not R1
[6 marks]
Examiners report
[N/A]
[N/A]
