Question
(a) Show that {1, −1, i, −i} forms a group of complex numbers G under multiplication.
(b) Consider \(S = \{ e,{\text{ }}a,{\text{ }}b,{\text{ }}a * b\} \) under an associative operation \( * \) where e is the identity element. If \(a * a = b * b = e\) and \(a * b = b * a\) , show that
(i) \(a * b * a = b\) ,
(ii) \(a * b * a * b = e\) .
(c) (i) Write down the Cayley table for \(H = \{ S{\text{ , }} * \} \).
(ii) Show that H is a group.
(iii) Show that H is an Abelian group.
(d) For the above groups, G and H , show that one is cyclic and write down why the other is not. Write down all the generators of the cyclic group.
(e) Give a reason why G and H are not isomorphic.
▶️Answer/Explanation
Markscheme
(a)
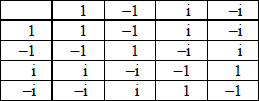
see the Cayley table, (since there are no new elements) the set is closed A1
1 is the identity element A1
1 and –1 are self inverses and i and -i form an inverse pair, hence every element has an inverse A1
multiplication is associative A1
hence {1, –1, i, –i} form a group G under the operation of multiplication AG
[4 marks]
(b) (i) aba = aab
= eb A1
= b AG
(ii) abab = aabb
= ee A1
= e AG
[2 marks]
(c) (i)
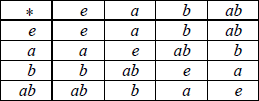 A2
A2
Note: Award A1 for 1 or 2 errors, A0 for more than 2.
(ii) see the Cayley table, (since there are no new elements) the set is closed A1
H has an identity element e A1
all elements are self inverses, hence every element has an inverse A1
the operation is associative as stated in the question
hence {e , a , b , ab} forms a group G under the operation \( * \) AG
(iii) since there is symmetry across the leading diagonal of the group table, the group is Abelian A1
[6 marks]
(d) consider the element i from the group G (M1)
\({{\text{i}}^2} = – 1\)
\({{\text{i}}^3} = – {\text{i}}\)
\({{\text{i}}^4} = 1\)
thus i is a generator for G and hence G is a cyclic group A1
–i is the other generator for G A1
for the group H there is no generator as all the elements are self inverses R1
[4 marks]
(e) since one group is cyclic and the other group is not, they are not isomorphic R1
[1 mark]
Total [17 marks]
Examiners report
Most candidates were aware of the group axioms and the properties of a group, but they were not always explained clearly. A number of candidates did not understand the term “Abelian”. Many candidates understood the conditions for a group to be cyclic. Many candidates did not realise that the answer to part (e) was actually found in part (d), hence the reason for this part only being worth 1 mark. Overall, a number of fully correct solutions to this question were seen.
Question
Let G be a finite cyclic group.
(a) Prove that G is Abelian.
(b) Given that a is a generator of G, show that \({a^{ – 1}}\) is also a generator.
(c) Show that if the order of G is five, then all elements of G, apart from the identity, are generators of G.
▶️Answer/Explanation
Markscheme
(a) let a be a generator and consider the (general) elements \(b = {a^m},{\text{ }}c = {a^n}\) M1
then
\(bc = {a^m}{a^n}\) A1
\( = {a^n}{a^m}\) (using associativity) R1
\( = cb\) A1
therefore G is Abelian AG
[4 marks]
(b) let G be of order p and let \(m \in \{ 1,…….,{\text{ }}p\} \), let a be a generator
consider \(a{a^{ – 1}} = e \Rightarrow {a^m}{({a^{ – 1}})^m} = e\) M1R1
this shows that \({({a^{ – 1}})^m}\) is the inverse of \({a^m}\) R1
as m increases from 1 to p, \({a^m}\) takes p different values and it generates G R1
it follows from the uniqueness of the inverse that \({({a^{ – 1}})^m}\) takes p different values and is a generator R1
[5 marks]
(c) EITHER
by Lagrange, the order of any element divides the order of the group, i.e. 5 R1
the only numbers dividing 5 are 1 and 5 R1
the identity element is the only element of order 1 R1
all the other elements must be of order 5 R1
so they all generate G AG
OR
let a be a generator.
successive powers of a and therefore the elements of G are
\(a,{\text{ }}{a^2},{\text{ }}{a^3},{\text{ }}{a^4}{\text{ and }}{a^5} = e\) A1
successive powers of \({a^2}\) are \({a^2},{\text{ }}{a^4},{\text{ }}a,{\text{ }}{a^3},{\text{ }}{a^5} = e\) A1
successive powers of \({a^3}\) are \({a^3},{\text{ }}a,{\text{ }}{a^4},{\text{ }}{a^2},{\text{ }}{a^5} = e\) A1
successive powers of \({a^4}\) are \({a^4},{\text{ }}{a^3},{\text{ }}{a^2},{\text{ }}a,{\text{ }}{a^5} = e\) A1
this shows that \({a^2},{\text{ }}{a^3},{\text{ }}{a^4}\) are also generators in addition to a AG
[4 marks]
Total [13 marks]
Examiners report
Solutions to (a) were often disappointing with some solutions even stating that a cyclic group is, by definition, commutative and therefore Abelian. Explanations in (b) were often poor and it was difficult in some cases to distinguish between correct and incorrect solutions. In (c), candidates who realised that Lagrange’s Theorem could be used were generally the most successful. Solutions again confirmed that, in general, candidates find theoretical questions on this topic difficult.
