Question
Find the set of values of k for which the improper integral \(\int_2^\infty {\frac{{{\text{d}}x}}{{x{{(\ln x)}^k}}}} \) converges.[6]
Show that the series \(\sum\limits_{r = 2}^\infty {\frac{{{{( – 1)}^r}}}{{r\ln r}}} \) is convergent but not absolutely convergent.[5]
▶️Answer/Explanation
Markscheme
consider the limit as \(R \to \infty \) of the (proper) integral
\(\int_2^R {\frac{{{\text{d}}x}}{{x{{(\ln x)}^k}}}} \) (M1)
substitute \(u = \ln x,{\text{ d}}u = \frac{1}{x}{\text{d}}x\) (M1)
obtain \(\int_{\ln 2}^{\ln R} {\frac{1}{{{u^k}}}{\text{d}}u = \left[ { – \frac{1}{{k – 1}}\frac{1}{{{u^{k – 1}}}}} \right]_{\ln 2}^{\ln R}} \) A1
Note: Ignore incorrect limits or omission of limits at this stage.
or \([\ln u]_{\ln 2}^{\ln R}\) if k = 1 A1
Note: Ignore incorrect limits or omission of limits at this stage.
because \(\ln R{\text{ }}({\text{and }}\ln \ln R) \to \infty {\text{ as }}R \to \infty \) (M1)
converges in the limit if k > 1 A1
[6 marks]
C: \({\text{terms}} \to 0{\text{ as }}r \to \infty \) A1
\(\left| {{u_{r + 1}}} \right| < \left| {{u_r}} \right|\) for all r A1
convergence by alternating series test R1
AC: \({(x\ln x)^{ – 1}}\) is positive and decreasing on \([2,\,\infty )\) A1
not absolutely convergent by integral test using part (a) for k = 1 R1
[5 marks]
Examiners report
A good number of candidates were able to find the integral in part (a) although the vast majority did not consider separately the integral when k = 1. Many candidates did not explicitly set a limit for the integral to let this limit go to infinity in the anti – derivative and it seemed that some candidates were “substituting for infinity”. This did not always prevent candidates finding a correct final answer but the lack of good technique is a concern. In part (b) many candidates seemed to have some knowledge of the relevant test for convergence but this test was not always rigorously applied. In showing that the series was not absolutely convergent candidates were often not clear in showing that the function being tested had to meet a number of criteria and in so doing lost marks.
A good number of candidates were able to find the integral in part (a) although the vast majority did not consider separately the integral when k = 1. Many candidates did not explicitly set a limit for the integral to let this limit go to infinity in the anti – derivative and it seemed that some candidates were “substituting for infinity”. This did not always prevent candidates finding a correct final answer but the lack of good technique is a concern. In part (b) many candidates seemed to have some knowledge of the relevant test for convergence but this test was not always rigorously applied. In showing that the series was not absolutely convergent candidates were often not clear in showing that the function being tested had to meet a number of criteria and in so doing lost marks.
Question
Consider the infinite series \(S = \sum\limits_{n = 0}^\infty {{u_n}} \) where \({u_n} = \int_{nx}^{(n + 1)\pi } {\frac{{\sin t}}{t}{\text{d}}t} \).
Explain why the series is alternating.
(i) Use the substitution \(T = t – \pi \) in the expression for \({u_{n + 1}}\) to show that \(\left| {{u_{n + 1}}} \right| < \left| {{u_n}} \right|\).
(ii) Show that the series is convergent.
Show that \(S < 1.65\).
▶️Answer/Explanation
Markscheme
as \(t\) moves through the intervals \([0,{\text{ }}\pi ],{\text{ }}[\pi ,{\text{ }}2\pi ],{\text{ }}[2\pi ,{\text{ }}3\pi ],{\text{ }}[3\pi ,{\text{ }}4\pi ]\), etc, the sign of \(\sin t\), (and therefore the sign of the integral) alternates \( + ,{\text{ }} – ,{\text{ }} + ,{\text{ }} – \), etc, so that the series is alternating R1
Note: Award R1 only if it includes a clear reason that justifies that the sign of the integrand alternates between − and + and this pattern is valid for all the terms.
The change of signs can be justified by a labelled graph of \(y = \sin (x)\) or \(y = \frac{{\sin x}}{x}\) that shows the intervals \([0,{\text{ }}\pi ],{\text{ }}[\pi ,{\text{ }}2\pi ],{\text{ }}[2\pi ,{\text{ }}3\pi ],{\text{ }} \ldots \)
[1 mark]
(i) \({u_{n + 1}} = \int_{(n + 1)\pi }^{(n + 2)\pi } {\frac{{\sin t}}{t}{\text{d}}t} \)
(M1)
put \(T = t–\pi \) and \({\text{d}}T = {\text{d}}t\) (M1)
the limits change to \(n\pi ,{\text{ }}(n + 1)\pi \)
\(\left| {{u_{n + 1}}} \right| = \int_{n\pi }^{(n + 1)\pi } {\frac{{\left| {\sin (T + \pi )} \right|}}{{T + \pi }}{\text{d}}T} \) (or equivalent) A1
\(\left| {\sin (T + \pi )} \right| = \left| {\sin (T)} \right|\) or \(\sin (T + \pi ) = – \sin (T)\) (M1)
\( = \int_{n\pi }^{(n + 1)\pi } {\frac{{\left| {\sin T} \right|}}{{T + \pi }}{\text{d}}T} \)
\( < \int_{n\pi }^{(n + 1)\pi } {\frac{{\left| {\sin T} \right|}}{T}{\text{d}}T = \left| {{u_n}} \right|} \) A1AG
(ii) \(\left| {{u_n}} \right| = \int_{n\pi }^{(n + 1)\pi } {\frac{{\sin t}}{t}{\text{d}}t} \)
\( < \int_{n\pi }^{(n + 1)\pi } {\frac{1}{t}{\text{d}}t} \) M1
\( = [\ln t]_{n\pi }^{(n + 1)\pi }\) A1
\( = \ln \left( {\frac{{n + 1}}{n}} \right)\) A1
\( \to \ln 1 = 0\) as \(n \to \infty \)
from part (i) \(\left| {{u_n}} \right|\) is a decreasing sequence and since \(\mathop {\lim }\limits_{n \to \infty } \left| {{u_n}} \right| = 0\), R1
the series is convergent AG
[9 marks]
attempt to calculate the partial sums \(\sum\limits_{i = 0}^{n – 1} {{u_i} = \int_0^{n\pi } {\frac{{\sin t}}{t}{\text{d}}t} } \) (M1)
the first partial sums are
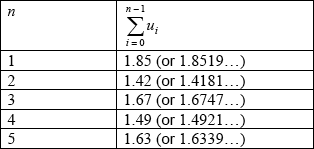
two consecutive partial sums for \(n \geqslant 4\) A1A1
(eg \({S_4} = 1.49\) and \({S_5} = 1.63\) or \({S_{100}} = 1.567 \ldots \) and \({S_{101}} = 1.573 \ldots \))
Note: These answers must be given to a minimum of 3 significant figures.
the sum to infinity lies between any two consecutive partial sums,
eg between 1.49 and 1.63 R1
so that \(S < 1.65\) AG
Note: Award A1A1R1 to candidates who calculate at least two partial sums for only odd values of \(n\) and state that the upper bound is less than these values.
[4 marks]
Examiners report
Very few candidates presented a valid reason to justify the alternating nature of the series. In most cases candidates just reformulated the wording of the question by saying that it changed signs and completely ignored the interval over which the expression had to be integrated to obtain each term.
(i) Most candidates achieved 1 or 2 marks for attempting the given substitution; in most cases candidates failed to find the correct limits of integration for the new variable and then relate the expressions of the consecutive terms of the series. In part (ii) very few correct attempts were seen; in some cases candidates did recognize the conditions for the alternating series to be convergent but very few got close to establish that the limit of the general term was zero.
A few good attempts to use partial sums were seen although once again candidates showed difficulties in identifying what was needed to show the given answer. In most cases candidates just verified with GDC that in fact for high values of n the series was indeed less than the upper bound given but could not provide a valid argument that justified the given statement.
Question
Consider the infinite spiral of right angle triangles as shown in the following diagram.
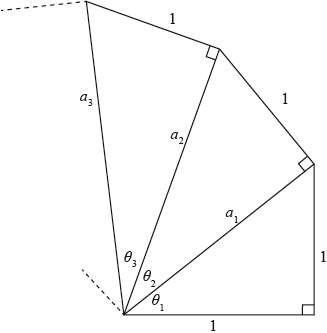
The \(n{\text{th}}\) triangle in the spiral has central angle \({\theta _n}\), hypotenuse of length \({a_n}\) and opposite side of length 1, as shown in the diagram. The first right angle triangle is isosceles with the two equal sides being of length 1.
Consider the series \(\sum\limits_{n = 1}^\infty {{\theta _n}} \).
a.Using l’Hôpital’s rule, find \(\mathop {\lim }\limits_{x \to \infty } \left( {\frac{{\arcsin \left( {\frac{1}{{\sqrt {(x + 1)} }}} \right)}}{{\frac{1}{{\sqrt x }}}}} \right)\).[6]
b.(i) Find \({a_1}\) and \({a_2}\) and hence write down an expression for \({a_n}\).
(ii) Show that \({\theta _n} = \arcsin \frac{1}{{\sqrt {(n + 1)} }}\).[3]
c.Using a suitable test, determine whether this series converges or diverges.[6]
▶️Answer/Explanation
Markscheme
\(\mathop {\lim }\limits_{x \to \infty } \left( {\frac{{\arcsin \left( {\frac{1}{{\sqrt {(x + 1)} }}} \right)}}{{\frac{1}{{\sqrt x }}}}} \right)\) is of the form \(\frac{0}{0}\)
and so will equal the limit of \(\frac{{\frac{{\frac{{ – 1}}{2}{{(x + 1)}^{ – \frac{3}{2}}}}}{{\sqrt {1 – \left( {\frac{1}{{x + 1}}} \right)} }}}}{{\frac{{ – 1}}{2}{x^{ – \frac{3}{2}}}}}\) M1M1A1A1
Note: M1 for attempting differentiation of the top and bottom, M1A1 for derivative of top (only award M1 if chain rule is used), A1 for derivative of bottom.
\( = \mathop {\lim }\limits_{x \to \infty } \frac{{{{\left( {\frac{x}{{(x + 1)}}} \right)}^{\frac{3}{2}}}}}{{\sqrt {\frac{x}{{x + 1}}} }} = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{x}{{x + 1}}} \right)\) M1
Note: Accept any intermediate tidying up of correct derivative for the method mark.
\( = 1\) A1
[6 marks]
(i) \({a_1} = \sqrt 2 ,{\text{ }}{a_2} = \sqrt 3 \) A1
\({a_n} = \sqrt {n + 1} \) A1
(ii) \(\sin {\theta _n} = \frac{1}{{{a_n}}} = \frac{1}{{\sqrt {n + 1} }}\) A1
Note: Allow \({\theta _n} = \arcsin \left( {\frac{1}{{{a_n}}}} \right)\) if \({a_n} = \sqrt {n + 1} \) in b(i).
so \({\theta _n} = \arcsin \frac{1}{{\sqrt {(n + 1)} }}\) AG
[3 marks]
for \(\sum\limits_{n = 1}^\infty {\arcsin \frac{1}{{\sqrt {(n + 1)} }}} \) apply the limit comparison test (since both series of positive terms) M1
with \(\sum\limits_{n = 1}^\infty {\frac{1}{{\sqrt n }}} \) A1
from (a) \(\mathop {\lim }\limits_{n \to \infty } \frac{{\arcsin \frac{1}{{\sqrt {(n + 1)} }}}}{{\frac{1}{{\sqrt n }}}} = 1\), so the two series either both converge or both diverge M1R1
\(\sum\limits_{n = 1}^\infty {\frac{1}{{\sqrt 2 }}} \) diverges (as is a \(p\)-series with \(p = \frac{1}{2}\)) A1
hence \(\sum\limits_{n = 1}^\infty {{\theta _n}} \) diverges A1
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
a.Given that \(n > {\text{ln}}\,n\) for \(n > 0\), use the comparison test to show that the series \(\sum\limits_{n = 0}^\infty {\frac{1}{{{\text{ln}}\left( {n + 2} \right)}}} \) is divergent.[3]
b.Find the interval of convergence for \(\sum\limits_{n = 0}^\infty {\frac{{{{\left( {3x} \right)}^n}}}{{{\text{ln}}\left( {n + 2} \right)}}} \).[7]
▶️Answer/Explanation
Markscheme
METHOD 1
\({\text{ln}}\left( {n + 2} \right) < n + 2\) (A1)
\( \Rightarrow \frac{1}{{{\text{ln}}\left( {n + 2} \right)}} > \frac{1}{{n + 2}}\) (for \(n \geqslant 0\)) A1
Note: Award A0 for statements such as \(\sum\limits_{n = 0}^\infty {\frac{1}{{{\text{ln}}\left( {n + 2} \right)}}} > \sum\limits_{n = 0}^\infty {\frac{1}{{n + 2}}} \). However condone such a statement if the above A1 has already been awarded.
\(\sum\limits_{n = 0}^\infty {\frac{1}{{n + 2}}} \) (is a harmonic series which) diverges R1
Note: The R1 is independent of the A1s.
Award R0 for statements such as “\(\frac{1}{{n + 2}}\) diverges”.
so \(\sum\limits_{n = 0}^\infty {\frac{1}{{{\text{ln}}\left( {n + 2} \right)}}} \) diverges by the comparison test AG
METHOD 2
\(\frac{1}{{{\text{ln}}\,n}} > \frac{1}{n}\) (for \(n \geqslant 2\)) A1
Note: Award A0 for statements such as \(\sum\limits_{n = 2}^\infty {\frac{1}{{{\text{ln}}\,n}}} > \sum\limits_{n = 2}^\infty {\frac{1}{n}} \). However condone such a statement if the above A1 has already been awarded.
a correct statement linking \(n\) and \(n + 2\) eg,
\(\sum\limits_{n = 0}^\infty {\frac{1}{{{\text{ln}}\left( {n + 2} \right)}}} = \sum\limits_{n = 2}^\infty {\frac{1}{{{\text{ln}}\,n}}} \) or \(\sum\limits_{n = 0}^\infty {\frac{1}{{n + 2}}} = \sum\limits_{n = 2}^\infty {\frac{1}{n}} \) A1
Note: Award A0 for \(\sum\limits_{n = 0}^\infty {\frac{1}{n}} \)
\(\sum\limits_{n = 2}^\infty {\frac{1}{n}} \) (is a harmonic series which) diverges
(which implies that \(\sum\limits_{n = 2}^\infty {\frac{1}{{{\text{ln}}\,n}}} \) diverges by the comparison test) R1
Note: The R1 is independent of the A1s.
Award R0 for statements such as \(\sum\limits_{n = 0}^\infty {\frac{1}{n}} \) deiverges and “\({\frac{1}{n}}\) diverges”.
Award A1A0R1 for arguments based on \(\sum\limits_{n = 1}^\infty {\frac{1}{n}} \).
so \(\sum\limits_{n = 0}^\infty {\frac{1}{{{\text{ln}}\left( {n + 2} \right)}}} \) diverges by the comparison test AG
[3 marks]
applying the ratio test \(\mathop {{\text{lim}}}\limits_{n \to \infty } \left| {\frac{{{{\left( {3x} \right)}^{n + 1}}}}{{{\text{ln}}\left( {n + 3} \right)}} \times \frac{{{\text{ln}}\left( {n + 2} \right)}}{{{{\left( {3x} \right)}^n}}}} \right|\) M1
\( = \left| {3x} \right|\) (as \(\mathop {{\text{lim}}}\limits_{n \to \infty } \left| {\frac{{{\text{ln}}\left( {n + 2} \right)}}{{{\text{ln}}\left( {n + 3} \right)}}} \right| = 1\) A1
Note: Condone the absence of limits and modulus signs.
Note: Award M1A0 for \(3{x^n}\). Subsequent marks can be awarded.
series converges for \( – \frac{1}{3} < x < \frac{1}{3}\)
considering \(x = – \frac{1}{3}\) and \(x = \frac{1}{3}\) M1
Note: Award M1 to candidates who consider one endpoint.
when \(x = \frac{1}{3}\), series is \(\sum\limits_{n = 0}^\infty {\frac{1}{{{\text{ln}}\left( {n + 2} \right)}}} \) which is divergent (from (a)) A1
Note: Award this A1 if \(\sum\limits_{n = 0}^\infty {\frac{1}{{{\text{ln}}\left( {n + 2} \right)}}} \) is not stated but reference to part (a) is.
when \(x = – \frac{1}{3}\), series is \(\sum\limits_{n = 0}^\infty {\frac{{{{\left( { – 1} \right)}^n}}}{{{\text{ln}}\left( {n + 2} \right)}}} \) A1
\(\sum\limits_{n = 0}^\infty {\frac{{{{\left( { – 1} \right)}^n}}}{{{\text{ln}}\left( {n + 2} \right)}}} \) converges (conditionally) by the alternating series test R1
(strictly alternating, \(\left| {{u_n}} \right| > \left| {{u_{n + 1}}} \right|\) for \(n \geqslant 0\) and \(\mathop {{\text{lim}}}\limits_{n \to \infty } \left( {{u_n}} \right) = 0\))
so the interval of convergence of S is \( – \frac{1}{3} \leqslant x < \frac{1}{3}\) A1
Note: The final A1 is dependent on previous A1s – ie, considering correct series when \(x = – \frac{1}{3}\) and \(x = \frac{1}{3}\) and on the final R1.
Award as above to candidates who firstly consider \(x = – \frac{1}{3}\) and then state conditional convergence implies divergence at \(x = \frac{1}{3}\).
[7 marks]
Examiners report
[N/A]
[N/A]
