Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.4\) .
a.Find the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.[4]
b.Given that \({\text{P}}(A \cup B) = 0.6\) , find \({\text{P}}(A|B)\) .[3]
▶️Answer/Explanation
Markscheme
(i) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) = 0.7\) A1
(ii) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) (M1)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = 0.3 + 0.4 – 0.12 = 0.58\) A1
[4 marks]
\({\text{P}}(A \cap B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cup B)\)
\( = 0.3 + 0.4 – 0.6 = 0.1\) A1
\({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\) (M1)
\( = \frac{{0.1}}{{0.4}} = 0.25\) A1
[3 marks]
Examiners report
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Question
In a population of rabbits, \(1\%\) are known to have a particular disease. A test is developed for the disease that gives a positive result for a rabbit that does have the disease in \(99\%\) of cases. It is also known that the test gives a positive result for a rabbit that does not have the disease in \(0.1\%\) of cases. A rabbit is chosen at random from the population.
a.Find the probability that the rabbit tests positive for the disease.[2]
b.Given that the rabbit tests positive for the disease, show that the probability that the rabbit does not have the disease is less than 10 %.[3]
▶️Answer/Explanation
Markscheme
R is ‘rabbit with the disease’
P is ‘rabbit testing positive for the disease’
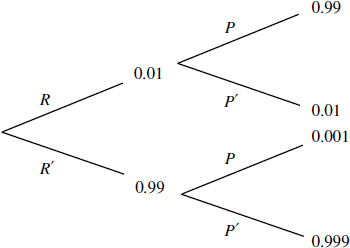
\({\text{P}}(P) = P(R \cap P) + P(R’ \cap P)\)
\( = 0.01 \times 0.99 + 0.99 \times 0.001\) M1
\( = 0.01089( = 0.0109)\) A1
Note: Award M1 for a correct tree diagram with correct probability values shown.
[2 marks]
R is ‘rabbit with the disease’
P is ‘rabbit testing positive for the disease’
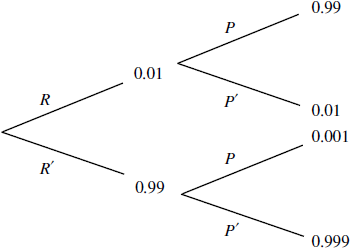
\(P(R’|P) = \frac{{0.001 \times 0.99}}{{0.001 \times 0.99 + 0.01 \times 0.99}}\left( { = \frac{{0.00099}}{{0.01089}}} \right)\) M1A1
\(\frac{{0.00099}}{{0.01089}} < \frac{{0.001}}{{0.01}} = 10\% \) (or other valid argument) R1
[3 marks]
Examiners report
There was a mixed performance in this question with some candidates showing good understanding of probability and scoring well and many others showing no understanding of conditional probability and difficulties in working with decimals. Very few candidates were able to provide a valid argument to justify their answer to part (b).
There was a mixed performance in this question with some candidates showing good understanding of probability and scoring well and many others showing no understanding of conditional probability and difficulties in working with decimals. Very few candidates were able to provide a valid argument to justify their answer to part (b).
Question
In a particular city 20 % of the inhabitants have been immunized against a certain disease. The probability of infection from the disease among those immunized is \(\frac{1}{{10}}\), and among those not immunized the probability is \(\frac{3}{4}\). If a person is chosen at random and found to be infected, find the probability that this person has been immunized.
▶️Answer/Explanation
Markscheme
tree diagram (M1)
\({\text{P(I|D)}} = \frac{{{\text{P(D|I)}} \times {\text{P(I)}}}}{{{\text{P(D)}}}}\) (M1)
\( = \frac{{0.1 \times 0.2}}{{0.1 \times 0.2 + 0.8 \times 0.75}}\) A1A1A1
\(\left( { = \frac{{0.02}}{{0.62}}} \right) = \frac{1}{{31}}\) A1
Note: Alternative presentation of results: M1 for labelled tree; A1 for initial branching probabilities, 0.2 and 0.8; A1 for at least the relevant second branching probabilities, 0.1 and 0.75; A1 for the ‘infected’ end-point probabilities, 0.02 and 0.6; M1A1 for the final conditional probability calculation.
[6 marks]
Examiners report
Candidates who drew a tree diagram, the majority, usually found the correct answer.
Question
On a particular day, the probability that it rains is \(\frac{2}{5}\) . The probability that the “Tigers” soccer team wins on a day when it rains is \(\frac{2}{7}\) and the probability that they win on a day when it does not rain is \(\frac{4}{7}\).
a.Draw a tree diagram to represent these events and their outcomes.[1]
b.What is the probability that the “Tigers” soccer team wins?[2]
c.Given that the “Tigers” soccer team won, what is the probability that it rained on that day?[2]
▶️Answer/Explanation
Markscheme
let R be “it rains” and W be “the ‘Tigers’ soccer team win”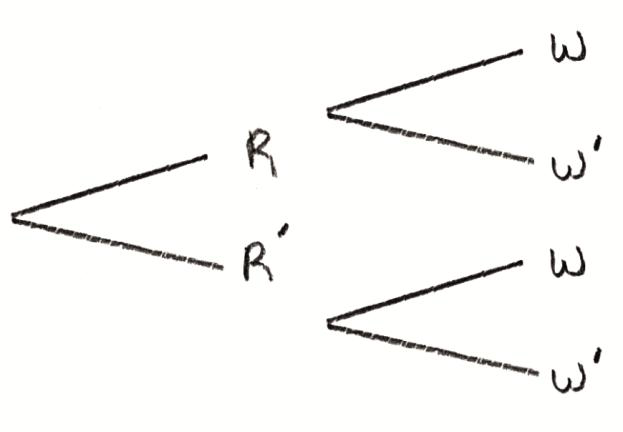 A1
A1
[1 mark]
\({\text{P}}(W) = \frac{2}{5} \times \frac{2}{7} + \frac{3}{5} \times \frac{4}{7}\) (M1)
\( = \frac{{16}}{{35}}\) A1
[2 marks]
\({\text{P}}(R\left| W \right.) = \frac{{\frac{2}{5} \times \frac{2}{7}}}{{\frac{{16}}{{35}}}}\) (M1)
\( = \frac{1}{4}\) A1
[2 marks]
Examiners report
This question was well answered in general.
This question was well answered in general.
This question was well answered in general.
Question
Two events A and B are such that \({\text{P}}(A \cup B) = 0.7\) and \({\text{P}}(A|B’) = 0.6\).
Find \({\text{P}}(B)\).
▶️Answer/Explanation
Markscheme
Note: Be aware that an unjustified assumption of independence will also lead to P(B) = 0.25, but is an invalid method.
METHOD 1
\({\text{P}}(A’|B’) = 1 – {\text{P}}(A|B’) = 1 – 0.6 = 0.4\) M1A1
\({\text{P}}(A’|B’) = \frac{{{\text{P}}(A’ \cap B’)}}{{{\text{P}}(B’)}}\)
\({\text{P}}(A’ \cap B’) = {\text{P}}\left( {(A \cup B)’} \right) = 1 – 0.7 = 0.3\) A1
\(0.4 = \frac{{0.3}}{{{\text{P}}(B’)}} \Rightarrow {\text{P(}}B’) = 0.75\) (M1)A1
\({\text{P}}(B) = 0.25\) A1
(this method can be illustrated using a tree diagram)
[6 marks]
METHOD 2
\({\text{P}}\left( {(A \cup B)’} \right) = 1 – 0.7 = 0.3\) A1
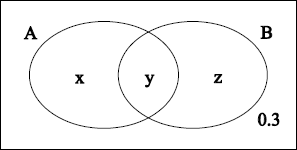
\({\text{P}}(A|B’) = \frac{x}{{x + 0.3}} = 0.6\) M1A1
\(x = 0.6x + 0.18\)
\(0.4x = 0.18\)
\(x = 0.45\) A1
\({\text{P}}(A \cup B) = x + y + z\)
\({\text{P}}(B) = y + z = 0.7 – 0.45\) (M1)
\( = 0.25\) A1
[6 marks]
METHOD 3
\(\frac{{{\text{P}}(A \cap B’)}}{{{\text{P}}(B’)}} = 0.6{\text{ (or P}}(A \cap B’) = 0.6{\text{P}}(B’)\) M1
\({\text{P}}(A \cap B’) = {\text{P}}(A \cup B) – {\text{P}}(B)\) M1A1
\({\text{P}}(B’) = 1 – {\text{P}}(B)\)
\(0.7 – {\text{P}}(B) = 0.6 – 0.6{\text{P}}(B)\) M1(A1)
\(0.1 = 0.4{\text{P}}(B)\)
\({\text{P}}(B) = \frac{1}{4}\) A1
[6 marks]
Examiners report
There is a great variety of ways to approach this question and there were plenty of very good solutions produced, all of which required an insight into the structure of conditional probability. A few candidates unfortunately assumed independence and so did not score well.
Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = \frac{2}{5},{\text{ P}}(B) = \frac{{11}}{{20}}\) and \({\text{P}}(A|B) = \frac{2}{{11}}\).
(a) Find \({\text{P}}(A \cap B)\).
(b) Find \({\text{P}}(A \cup B)\).
(c) State with a reason whether or not events \(A\) and \(B\) are independent.
▶️Answer/Explanation
Markscheme
(a) \({\text{P}}(A \cap B) = {\text{P}}(A|B) \times P(B)\)
\({\text{P}}(A \cap B) = \frac{2}{{11}} \times \frac{{11}}{{20}}\) (M1)
\( = \frac{1}{{10}}\) A1
[2 marks]
(b) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\)
\({\text{P}}(A \cup B) = \frac{2}{5} + \frac{{11}}{{20}} – \frac{1}{{10}}\) (M1)
\( = \frac{{17}}{{20}}\) A1
[2 marks]
(c) No – events A and B are not independent A1
EITHER
\({\text{P}}(A|B) \ne {\text{P}}(A)\) R1
\(\left( {\frac{2}{{11}} \ne \frac{2}{5}} \right)\)
OR
\({\text{P}}(A) \times {\text{P}}(B) \ne {\text{P}}(A \cap B)\)
\(\frac{2}{5} \times \frac{{11}}{{20}} = \frac{{11}}{{50}} \ne \frac{1}{{10}}\) R1
Note: The numbers are required to gain R1 in the ‘OR’ method only.
Note: Do not award A1R0 in either method.
[2 marks]
Total [6 marks]
Examiners report
Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.2\) and \({\text{P}}(B) = 0.5\).
a.Determine the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.[4]
b.Determine the range of possible values of \({\text{P}}\left( {A|B} \right)\).[3]
▶️Answer/Explanation
Markscheme
(i) use of \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B)\) (M1)
\({\text{P}}(A \cup B) = 0.2 + 0.5\)
\( = 0.7\) A1
(ii) use of \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\({\text{P}}(A \cup B) = 0.2 + 0.5 – 0.1\)
\( = 0.6\) A1
[4 marks]
\({\text{P}}\left( {A|B} \right) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\)
\({\text{P}}\left( {A|B} \right)\) is a maximum when \({\text{P}}(A \cap B) = {\text{P}}(A)\)
\({\text{P}}\left( {A|B} \right)\) is a minimum when \({\text{P}}(A \cap B) = 0\)
\(0 \le {\text{P}}\left( {A|B} \right) \le 0.4\) A1A1A1
Note: A1 for each endpoint and A1 for the correct inequalities.
[3 marks]
Total [7 marks]
Examiners report
This part was generally well done.
Disappointingly, many candidates did not seem to understand the meaning of the word ‘range’ in this context.
Question
Two events \(A\) and \(B\) are such that \({\text{P}}(A \cap B’) = 0.2\) and \({\text{P}}(A \cup B) = 0.9\).
a.On the Venn diagram shade the region \(A’ \cap B’\).
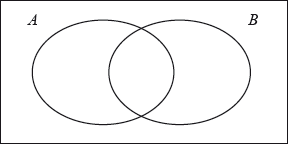 [1]
[1]
b.Find \({\text{P}}(A’|B’)\).[4]
▶️Answer/Explanation
Markscheme
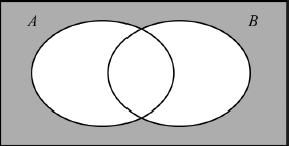 A1
A1
[1 mark]
\(P(A’|B’) = \frac{{P(A’ \cap B’)}}{{P(B’)}}\) (M1)
\(P(B’) = 0.1 + 0.2 = 0.3\) (A1)
\(P(A’ \cap B’) = 0.1\) (A1)
\(P(A’|B’) = \frac{{0.1}}{{0.3}} = \frac{1}{3}\) A1
[4 marks]
Examiners report
Part (a) was well done.
In part (b) some candidates were unable to write down the conditional probability formula. Some then failed to realise that part (a) was designed to help them work out \(P(A’ \cap B’)\) and instead incorrectly assumed independence.
Question
\(A\) and \(B\) are independent events such that \({\text{P}}(A) = {\text{P}}(B) = p,{\text{ }}p \ne 0\).
a.Show that \({\text{P}}(A \cup B) = 2p – {p^2}\).[2]
b.Find \({\text{P}}(A|A \cup B)\) in simplest form.[4]
▶️Answer/Explanation
Markscheme
\({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = p + p – {p^2}\) A1
\( = 2p – {p^2}\) AG
[2 marks]
\({\text{P}}(A|A \cup B) = \frac{{{\text{P}}\left( {A \cap (A \cup B)} \right)}}{{{\text{P}}(A \cup B)}}\) (M1)
Note: Allow \({\text{P}}(A \cap A \cup B)\) if seen on the numerator.
\( = \frac{{{\text{P}}(A)}}{{{\text{P}}(A \cup B)}}\) (A1)
\( = \frac{p}{{2p – {p^2}}}\) A1
\( = \frac{1}{{2 – p}}\) A1
[4 marks]
Examiners report
Part (a) posed few problems. Part (b) was possibly a good discriminator for the 4/5 candidates. Some were aware of an alternative (useful) form for the conditional probability, but were unable to interpret \(P\left( {A \cap (A \cup B)} \right)\). Large numbers of fully correct answers were seen.
Part (a) posed few problems. Part (b) was possibly a good discriminator for the 4/5 candidates. Some were aware of an alternative (useful) form for the conditional probability, but were unable to interpret \(P\left( {A \cap (A \cup B)} \right)\). Large numbers of fully correct answers were seen.
Question
Consider two events \(A\) and \(A\) defined in the same sample space.
a.Given that \({\text{P}}(A \cup B) = \frac{4}{9},{\text{ P}}(B|A) = \frac{1}{3}\) and \({\text{P}}(B|A’) = \frac{1}{6}\),
Show that \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(A’ \cap B)\).[3]
b.(i) show that \({\text{P}}(A) = \frac{1}{3}\);
(ii) hence find \({\text{P}}(B)\).[6]
▶️Answer/Explanation
Markscheme
METHOD 1
\({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) M1
\( = {\text{P}}(A) + {\text{P}}(A \cap B) + {\text{P}}(A’ \cap B) – {\text{P}}(A \cap B)\) M1A1
\( = {\text{P}}(A) + {\text{P}}(A’ \cap B)\) AG
METHOD 2
\({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) M1
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A|B) \times {\text{P}}(B)\) M1
\( = {\text{P}}(A) + \left( {1 – {\text{P}}(A|B)} \right) \times {\text{P}}(B)\)
\( = {\text{P}}(A) + {\text{P}}(A’|B) \times {\text{P}}(B)\) A1
\( = {\text{P}}(A) + {\text{P}}(A’ \cap B)\) AG
[3 marks]
(i) use \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(A’ \cap B)\) and \({\text{P}}(A’ \cap B) = {\text{P}}(B|A’){\text{P}}(A’)\) (M1)
\(\frac{4}{9} = {\text{P}}(A) + \frac{1}{6}\left( {1 – {\text{P}}(A)} \right)\) A1
\(8 = 18{\text{P}}(A) + 3\left( {1 – {\text{P}}(A)} \right)\) M1
\({\text{P}}(A) = \frac{1}{3}\) AG
(ii) METHOD 1
\({\text{P}}(B) = {\text{P}}(A \cap B) + {\text{P}}(A’ \cap B)\) M1
\( = {\text{P}}(B|A){\text{P}}(A) + {\text{P}}(B|A’){\text{P}}(A’)\) M1
\( = \frac{1}{3} \times \frac{1}{3} + \frac{1}{6} \times \frac{2}{3} = \frac{2}{9}\) A1
METHOD 2
\({\text{P}}(A \cap B) = {\text{P}}(B|A){\text{P}}(A) \Rightarrow {\text{P}}(A \cap B) = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}\) M1
\({\text{P}}(B) = {\text{P}}(A \cup B) + {\text{P}}(A \cap B) – {\text{P}}(A)\) M1
\({\text{P}}(B) = \frac{4}{9} + \frac{1}{9} – \frac{1}{3} = \frac{2}{9}\) A1
[6 marks]
Examiners report
[N/A]
[N/A]
Question
A bag contains three balls numbered 1, 2 and 3 respectively. Bill selects one of these balls at random and he notes the number on the selected ball. He then tosses that number of fair coins.
a.Calculate the probability that no head is obtained.[3]
b.Given that no head is obtained, find the probability that he tossed two coins.[3]
▶️Answer/Explanation
Markscheme
P(no heads from n coins tossed) = \({0.5^n}\) (A1)
P(no head) = \(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3} \times \frac{1}{8}\) M1
= \(\frac{7}{{24}}\) A1
[3 marks]
\({\text{P(2 | no heads)}} = \frac{{{\text{P(2 coins and no heads)}}}}{{{\text{P(no heads)}}}}\) M1
\( = \frac{{\frac{1}{{12}}}}{{\frac{7}{{24}}}}\) A1
\( = \frac{2}{7}\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
