Question
Urea, (H2N)2CO, is excreted by mammals and can be used as a fertilizer.
a(i) Calculate the percentage by mass of nitrogen in urea to two decimal places using section 6 of the data booklet.[2]
a(ii) Suggest how the percentage of nitrogen affects the cost of transport of fertilizers giving a reason.[1]
b.
The structural formula of urea is (H2N)2CO. Draw its structure.
c.
Predict the electron domain and molecular geometries at the (i)nitrogen and (ii)carbon atoms in urea, applying the VSEPR theory.
[3]
(iii)
Urea can be made by reacting potassium cyanate, KNCO, with ammonium chloride, NH4Cl.
KNCO(aq) + NH4Cl(aq) → (H2N)2CO(aq) + KCl(aq)
Determine the maximum mass of urea that could be formed from 50.0 cm3 of 0.100 mol dm−3 potassium cyanate solution.[2]
2NH3(g) + CO2(g) \( \rightleftharpoons \) (H2N)2CO(g) + H2O(g) ΔH < 0
Predict, with a reason, the effect on the equilibrium constant, Kc, when the temperature is increased.[1]
Suggest one reason why urea is a solid and ammonia a gas at room temperature.[1]
Sketch two different hydrogen bonding interactions between ammonia and water.[2]
The combustion of urea produces water, carbon dioxide and nitrogen.
Formulate a balanced equation for the reaction.[2]
The mass spectrum of urea is shown below.
Identify the species responsible for the peaks at (i)m/z = 60 and (ii)m/z = 44.
[2]
The IR spectrum of urea is shown below.
Identify the bonds causing the absorptions at (i)3450 cm−1 and (ii)1700 cm−1 using section 26 of the data booklet.
[2]
i. Predict the number of signals in the 1H NMR spectrum of urea.[1]
▶️Answer/Explanation
Markscheme
a(i)
Molar mass of urea «= 4 × 1.01 + 2 × 14.01 + 12.01 + 16.00» = 60.07 «g mol–1»
«% nitrogen = \(\frac{{2 \times 14.01}}{{60.07}}\) × 100 =» 46.65 «%»
Award [2] for correct final answer.
Award [1 max] for final answer not to two decimal places.
[2 marks]
«cost» increases AND lower N% «means higher cost of transportation per unit of nitrogen»
OR
«cost» increases AND inefficient/too much/about half mass not nitrogen
Accept other reasonable explanations.
Do not accept answers referring to safety/explosions.
[1 mark]
b. 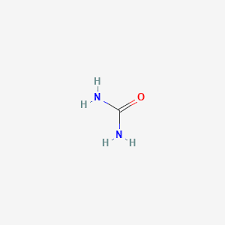
Note: Urea’s structure is more complex than that predicted from VSEPR theory.
[3 marks]
n(KNCO) «= 0.0500 dm3 × 0.100 mol dm–3» = 5.00 × 10–3 «mol»
«mass of urea = 5.00 × 10–3 mol × 60.07 g mol–1» = 0.300 «g»
Award [2] for correct final answer.
[2 marks]
«Kc» decreases AND reaction is exothermic
OR
«Kc» decreases AND ΔH is negative
OR
«Kc» decreases AND reverse/endothermic reaction is favoured
[1 mark]
Any one of:
urea has greater molar mass
urea has greater electron density/greater London/dispersion
urea has more hydrogen bonding
urea is more polar/has greater dipole moment
Accept “urea has larger size/greater van der Waals forces”.
Do not accept “urea has greater intermolecular forces/IMF”.
[1 mark]
Award [1] for each correct interaction.
If lone pairs are shown on N or O, then the lone pair on N or one of the lone pairs on O MUST be involved in the H-bond.
Penalize solid line to represent H-bonding only once.
[2 marks]
2(H2N)2CO(s) + 3O2(g) → 4H2O(l) + 2CO2(g) + 2N2(g)
correct coefficients on LHS
correct coefficients on RHS
Accept (H2N)2CO(s) + \(\frac{3}{2}\)O2(g) → 2H2O(l) + CO2(g) + N2(g).
Accept any correct ratio.
[2 marks]
i. 60: CON2H4+
ii. 44: CONH2+
Accept “molecular ion”.
[2 marks]
i. 3450 cm–1: N–H
ii. 1700 cm–1: C=O
Do not accept “O–H” for 3450 cm–1.
[2 marks]
[1 mark]
Weight considerations: Fertilizers are often transported in bulk, either by truck, rail, or ship. The weight of the fertilizer directly affects the cost of transportation, as heavier loads require more fuel and resources to move. Fertilizers with higher nitrogen percentages tend to be heavier because nitrogen is a relatively heavy element. Therefore, transporting fertilizers with a higher nitrogen content can result in higher transportation costs compared to fertilizers with lower nitrogen percentages.
Volume considerations: Fertilizers with higher nitrogen percentages generally have a higher nutrient concentration. This means that a smaller volume of high-nitrogen fertilizer can provide the same amount of nitrogen as a larger volume of low-nitrogen fertilizer. When it comes to transportation, volumetric efficiency is crucial. Transporting a smaller volume of fertilizer reduces the space needed and allows for more efficient use of storage capacity in vehicles and containers. Therefore, fertilizers with higher nitrogen percentages can be more cost-effective to transport since they require less volume for the same amount of nutrient content.

c(i)
Nitrogen (N) atom: The nitrogen atom in urea has four electron groups surrounding it: two N-H bonds, one N-C single bond, and one lone pair of electrons on the nitrogen atom.
Electron domain geometry: The electron domain geometry is tetrahedral since there are four electron groups around the nitrogen atom.
Molecular geometry: The molecular geometry is trigonal pyramidal since there is one lone pair of electrons on the nitrogen atom. The N-H bonds and N-C single bond are arranged in a pyramid-like shape.
c(ii)
Carbon (C) atom: The carbon atom in urea is double-bonded to oxygen (O) and single-bonded to two nitrogen (N) atoms.
Electron domain geometry: The carbon atom has three electron groups surrounding it: one C=O double bond and two C-N single bonds. The electron domain geometry is trigonal planar.
Molecular geometry: The molecular geometry is trigonal planar since there are three electron groups around the carbon atom. The C=O double bond and the two C-N single bonds are in the same plane.
c(iii).
KNCO(aq) + NH4Cl(aq) → (H2N)2CO(aq) + KCl(aq)
No of moles of KNCO = 0.0500 dm3 × 0.100 mol dm–3 = 0.005 moles
Here, 1 mole of KNCO forms 1 mole of urea.
So, 0.005 moles of urea are formed.
Mass of urea = 5.00 × 10–3 mol × 60.07 g mol–1 = 0.3 g.
d).
When the temperature of an exothermic reaction is increased, the reaction will proceed in the backward direction, so as to absorb heat and nullify the effect of increasing temperature. This will decrease the value of the equilibrium constant Kc. In other words, the equilibrium will shift to left.
e(i).
Urea (CH₄N₂O) is a polar molecule with hydrogen bonding capability. The presence of polar functional groups (such as the carbonyl group and amino groups) allows urea molecules to form hydrogen bonds with each other. These hydrogen bonds create strong intermolecular attractions, leading to a higher degree of cohesion between urea molecules. This cohesive force keeps urea molecules close together and results in a solid state at room temperature.
On the other hand, ammonia (NH₃) is a nonpolar molecule. Although ammonia has a polar N-H bond, the molecule’s shape and symmetry result in a cancellation of the overall dipole moment. As a result, ammonia molecules do not have significant dipole-dipole interactions or hydrogen bonding. The intermolecular forces in ammonia are relatively weak, resulting in a lower degree of cohesion between ammonia molecules. These weak forces allow ammonia molecules to move more freely and rapidly, resulting in a gaseous state at room temperature.
e(ii).
First, water donates a hydrogen bond to the lone pair of electrons on the nitrogen atom in ammonia (NH₃).
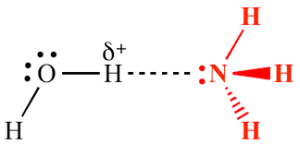
Second, Ammonia donates a hydrogen bond from one of its hydrogen atoms to the oxygen atom in water (H₂O).
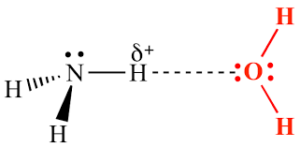
f. 2(H2N)2CO(s) + 3O2(g) → 4H2O(l) + 2CO2(g) + 2N2(g)
In this balanced equation, two molecules of urea (CH₄N₂O) reacts with three molecules of oxygen gas (O₂) to produce two molecules of carbon dioxide (CO₂), four molecules of water (H₂O), and two molecule of nitrogen gas (N₂). The equation is now balanced, with equal numbers of atoms on both sides.
The above equation divided by two is also correct. i.e. (H2N)2CO(s) + \(\frac{3}{2}\)O2(g) → 2H2O(l) + CO2(g) + N2(g).
g(i) In the mass spectrum of urea, the species at m/z = 60 corresponds to the molecular ion peak ([M]+) of urea. The m/z value of 60 indicates the mass-to-charge ratio of the ionized urea molecule. m/z = 60 represents CON2H4+.
g(ii) The species at m/z = 44 in the mass spectrum of urea corresponds to the fragment ion peak resulting from the loss of one (NH₂) molecule from the molecular ion. This fragment ion is often observed in the mass spectra of urea due to the tendency of urea to lose NH2 during ionization. m/z = 44 represents CONH2+.
h(i) The absorption at 3450 cm^(-1) is typically associated with the stretching vibration of the N-H bonds in urea. Urea has two amino groups (-NH₂) which can exhibit hydrogen bonding and lead to broad and strong absorption in this region.
h(ii) The absorption at 1700 cm^(-1) is associated with the stretching vibration of the carbonyl (C=O) group in urea. Urea contains a carbonyl group (C=O) in its structure, which is responsible for this characteristic absorption. The carbonyl stretching vibrations often occur in this frequency range.
i.
In urea (CH₄N₂O), there are no hydrogen atoms attached to carbon. The molecule contains two NH₂ groups attached to the carbonyl group (C=O). Each NH₂ group has two equivalent hydrogen atoms.
Therefore, in the ^1H NMR spectrum of urea, there will be one signal for the four equivalent NH₂ hydrogens.
Question
A student determined the percentage of the active ingredient magnesium hydroxide, Mg(OH)2, in a 1.24 g antacid tablet.
The antacid tablet was added to 50.00 cm3 of 0.100 mol dm−3 sulfuric acid, which was in excess.
a.Calculate the amount, in mol, of H2SO4.[1]
b.Formulate the equation for the reaction of H2SO4 with Mg(OH)2.[1]
The excess sulfuric acid required 20.80 cm3 of 0.1133 mol dm−3 NaOH for neutralization.
c.Calculate the amount of excess acid present.[1]
d.Calculate the amount of H2SO4 that reacted with Mg(OH)2.[1]
eDetermine the mass of Mg(OH)2 in the antacid tablet.[2].
f.Calculate the percentage by mass of magnesium hydroxide in the 1.24 g antacid tablet to three significant figures.[1]
▶️Answer/Explanation
Markscheme
a.n(H2SO4) «= 0.0500 dm3 × 0.100 mol dm–3» = 0.00500/5.00 × 10–3«mol»
[1 mark]
H2SO4(aq) + Mg(OH)2(s) → MgSO4(aq) + 2H2O(l)
Accept an ionic equation.
[1 mark]
«n(H2SO4) =\(\frac{1}{2}\) × n(NaOH) = \(\frac{1}{2}\) (0.02080 dm3 × 0.1133 mol dm–3)»
0.001178/1.178 × 10–3 «mol»
[1 mark]
n(H2SO4) reacted «= 0.00500 – 0.001178» = 0.00382/3.82 × 10–3 «mol»
[1 mark]
n(Mg(OH)2) «= n(H2SO4) =» = 0.00382/3.82 × 10–3 «mol»
m(Mg(OH)2) «= 0.00382 mol × 58.33 g mol–1» = 0.223 «g»
Award [2] for correct final answer.
[2 marks]
% Mg(OH)2 «= \(\frac{{0.223{\text{ g}}}}{{1.24{\text{ g}}}}\) × 100» = 18.0 «%»
Answer must show three significant figures.
[1 mark]
Detailed solutions:
a. 50.00 cm3 of 0.100 mol dm−3 sulfuric acid
Number of moles of H2SO4 = 0.050 dm3 *0.1 mol dm−3 = 0.005 moles.
b.
Reaction between sulfuric acid and magnesium hydroxide is an acid base reaction.
H2SO4(aq) + Mg(OH)2(s) → MgSO4(aq) + 2H2O(l)
c.
The excess sulfuric acid required 20.80 cm3 of 0.1133 mol dm−3 NaOH for neutralization.
Number of moles of OH– required for neutralization = Number of moles of H+ released by excess sulfuric acid.
Number of moles of NaOH = Number of moles of OH– = 0.02080 dm3 *0.1133 mol dm−3 = 0.002356 moles.
Now, 1 mole of sulfuric acid releases 2 moles of H+ ions.
Hence, Number of moles of excess sulfuric acid present = 0.5*0.002356 moles = 0.001178 moles.
d.
Number of moles of H2SO4 reacted with Mg(OH)2 = Number of moles of H2SO4 initially – Number of moles of excess sulfuric acid present
= 0.005-0.001178 = 0.003822 moles.
e.
Number of moles of H2SO4 reacted = Number of moles of Mg(OH)2 in the antacid tablet.
Mass of Mg(OH)2 in the antacid tablet = 0.003822 mol*58.33 g/mol = 0.223 g.
f.
% by mass of Mg(OH)2 in the 1.24 g antacid tablet = \(\frac{{0.223{\text{ g}}}}{{1.24{\text{ g}}}}\) × 100 = 18.0% (In three significant digits).