Question
Topic:
Discuss: How many moles of magnesium hydroxide are produced with $0.50 \mathrm{~mol}$ of ammonia?
$$
\mathrm{Mg}_3 \mathrm{~N}_2(\mathrm{~s})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow 3 \mathrm{Mg}(\mathrm{OH})_2(\mathrm{aq})+2 \mathrm{NH}_3(\mathrm{aq})
$$
A. $0.25$
B. $0.33$
C. $0.75$
D. $1.5$
▶️Answer/Explanation
Ans:C
Solution:
From the balanced chemical equation, it can be seen that 2 moles of ammonia are required to produce 3 moles of magnesium hydroxide. Therefore, if $0.50~\mathrm{mol}$ of ammonia is consumed, then the amount of magnesium hydroxide produced can be calculated as follows:
$$
\frac{3~\mathrm{mol~Mg(OH)_2}}{2~\mathrm{mol~NH_3}} \times 0.50~\mathrm{mol~NH_3} = 0.75~\mathrm{mol~Mg(OH)_2}
$$
Therefore, the answer is option C, $0.75$ moles of magnesium hydroxide.
Question
Topic:
Discuss: What is the sum of the integer coefficients when propene undergoes complete combustion?
$$
\ldots \mathrm{C_3} \mathrm{H}_6(\mathrm{~g})+\ldots \mathrm{O}_2(\mathrm{~g}) \rightarrow \ldots \mathrm{CO}_2(\mathrm{~g})+\ldots \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$$
A. $11$
B. $17$
C. $21$
D. $23$
▶️Answer/Explanation
Ans:D
Solution:
$2 \mathrm{C_3} \mathrm{H}_6(\mathrm{~g})+9 \mathrm{O}_2(\mathrm{~g}) \rightarrow 6 \mathrm{CO}_2(\mathrm{~g})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l})$
The sum of the coefficients in this balanced equation is $2+9+6+6=23$. Therefore, the answer is D. $23$.
Question
Topic:
Discuss: the volume of gas when the pressure on $100 \mathrm{~cm}^3$ of gas is changed from $400 \mathrm{kPa}$ to $200 \mathrm{kPa}$ at constant temperature?
A. $50.0 \mathrm{~cm}^3$
B. $100 \mathrm{~cm}^3$
C. $200 \mathrm{~cm}^3$
D. $800 \mathrm{~cm}^3$
▶️Answer/Explanation
Ans:C
Solution:
The relationship between pressure ($P$) and volume ($V$) of a gas at constant temperature can be described by the following equation:
$$
P_1V_1 = P_2V_2
$$
where $P_1$ and $V_1$ are the initial pressure and volume, and $P_2$ and $V_2$ are the final pressure and volume.
We are given $P_1 = 400\ \mathrm{kPa}$, $P_2 = 200\ \mathrm{kPa}$, and $V_1 = 100\ \mathrm{cm^3}$. To find $V_2$, we can rearrange the equation as follows:
$$
V_2 = \frac{P_1V_1}{P_2} = \frac{(400\ \mathrm{kPa})(100\ \mathrm{cm^3})}{200\ \mathrm{kPa}} = 200\ \mathrm{cm^3}
$$
Therefore, the volume of the gas when the pressure is changed from $400\ \mathrm{kPa}$ to $200\ \mathrm{kPa}$ at constant temperature is $200\ \mathrm{cm^3}$, and the answer is C. $200\ \mathrm{~cm^3}$.
Question
Topic:
Discuss: Which is correct for ${ }_{16}^{34} \mathrm{~S}^{2-} ?$
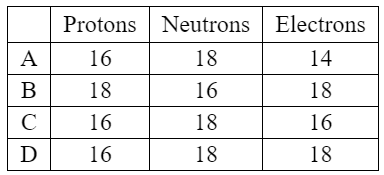
▶️Answer/Explanation
Ans:D
Solution:
The atomic number of an atom or ion is equal to the number of protons in its nucleus. In this case, since the ion is sulfur with a 2- charge, it has gained two electrons compared to a neutral sulfur atom. Therefore, the number of protons in the nucleus is still 16, while the number of electrons is 16 + 2 = 18.
The mass number of an atom or ion is equal to the sum of the number of protons and the number of neutrons in the nucleus. The atomic mass of sulfur is 34, so the sum of the number of protons and the number of neutrons in the nucleus of the sulfur ion is 34. Since the number of protons is 16, the number of neutrons is 34 – 16 = 18.
Therefore, the correct option is D, with 16 protons, 18 electrons, and 18 neutrons.
Question
Topic:
Discuss: Which of the following transitions in the hydrogen atom emits the least energy?
A. $\mathrm{n}=2$ to $\mathrm{n}=1$
B. $\mathrm{n}=3$ to $\mathrm{n}=1$
C. $\mathrm{n}=4$ to $\mathrm{n}=2$
D. $\mathrm{n}=4$ to $\mathrm{n}=3$
▶️Answer/Explanation
Ans:D
Solution:
The energy of a photon emitted during a transition from an initial energy level $\mathrm{n}_i$ to a final energy level $\mathrm{n}_f$ in a hydrogen atom can be calculated using the following equation:
$$
E = \frac{hcR}{\mathrm{n}_f^2 – \mathrm{n}_i^2}
$$
where $h$ is Planck’s constant, $c$ is the speed of light, $R$ is the Rydberg constant, and $\mathrm{n}_i$ and $\mathrm{n}_f$ are integers representing the initial and final energy levels, respectively.
We are asked to find the transition that emits the least energy, which means we are looking for the smallest value of $E$. From the given transitions, we can calculate the energies as follows:
A. $\mathrm{n}=2$ to $\mathrm{n}=1$: $E = \frac{hcR}{1^2 – 2^2} = 2.18 \times 10^{-18}\ \mathrm{J}$
B. $\mathrm{n}=3$ to $\mathrm{n}=1$: $E = \frac{hcR}{1^2 – 3^2} = 1.23 \times 10^{-18}\ \mathrm{J}$
C. $\mathrm{n}=4$ to $\mathrm{n}=2$: $E = \frac{hcR}{2^2 – 4^2} = 4.10 \times 10^{-19}\ \mathrm{J}$
D. $\mathrm{n}=4$ to $\mathrm{n}=3$: $E = \frac{hcR}{3^2 – 4^2} = 1.36 \times 10^{-19}\ \mathrm{J}$
Therefore, the transition that emits the least energy is option D, from $\mathrm{n}=4$ to $\mathrm{n}=3$, with an energy of $1.36 \times 10^{-19}\ \mathrm{J}$.