Question-1 :2021-may-Chemistry_paper_1__TZ1_HL
Topic:
Discuss: Which contains the most atoms of oxygen?
A. $64 \mathrm{~g}$ of $\mathrm{O}_2$
B. $1.2 \times 10^{24}$ molecules of $\mathrm{O}_2$
C. $64 \mathrm{~g}$ of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$
D. $1.2 \times 10^{24}$ molecules of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$
Answer/Explanation
Solution:
To determine which option contains the most atoms of oxygen, we need to calculate the total number of oxygen atoms in each option.
A. $64 \mathrm{~g}$ of $\mathrm{O}_2$: The molar mass of oxygen is $16 \mathrm{~g/mol}$. Therefore, $64 \mathrm{~g}$ of $\mathrm{O}_2$ contains $64 \mathrm{~g} /16 \mathrm{~g/mol} = 4$ moles of oxygen.
“1 mole of any element contains $6.022 \times 10^{23}$ atoms.”
$\therefore$ no. of atoms in 4 moles $\mathrm{O}_2=4 \times 6.022 \times 10^{23}=2.4088 \times 10^{24}$ atoms.
B. $1.2 \times 10^{24}$ molecules of $\mathrm{O}_2$: $1.2 \times 10^{24}$ molecules of $\mathrm{O}_2$ contain $1.2 \times 10^{24}$ molecules $\times 2$ atoms/molecule $= 2.4 \times 10^{24}$ atoms of oxygen.
C. $64 \mathrm{~g}$ of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$: The molar mass of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$ is $89 \mathrm{~g/mol}$. Therefore, $64 \mathrm{~g}$ of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$
contains $64 \mathrm{~g} / 89 \mathrm{~g/mol} = 0.719 \mathrm{~mol}$ of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$. Each mole of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$ contains $3$ atoms of oxygen, so $64 \mathrm{~g}$ of
$\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$ contains $0.719 \mathrm{~mol} \times 3 \mathrm{~atoms/mol} = 2.157 \mathrm{~mol}$ of oxygen atoms. The total number of oxygen atoms is $2.157 \mathrm{~mol} \times 6.02 \times 10^{23}\mathrm{~atoms/mol} = 1.298 \times 10^{24}$ atoms.
D. $1.2 \times 10^{24}$ molecules of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$: $1.2 \times 10^{24}$ molecules of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$ contain $1.2 \times 10^{24}$ molecules $\times 3$ atoms/molecule $= 3.6 \times 10^{24}$ atoms of oxygen.
Therefore, option D contains the most atoms of oxygen.
Question-2 :2021-may-Chemistry_paper_1__TZ1_HL
Topic:
Given: A sample of a compound contains approximately $24.0 \mathrm{~g} \mathrm{C}, 3.0 \mathrm{~g} \mathrm{H}$, and $1.6 \mathrm{~g} \mathrm{O}$.
Calculate: What is the empirical formula of the compound?
A. $\mathrm{C}_{20} \mathrm{H}_{30} \mathrm{O}$
B. $\mathrm{C}_{84} \mathrm{H}_{10} \mathrm{O}_6$
C. $\mathrm{C}_2 \mathrm{H}_3 \mathrm{O}$
D. $\mathrm{C}_{24} \mathrm{H}_{30} \mathrm{O}_2$
Answer/Explanation
Solution:
To determine the empirical formula of the compound, we need to find the smallest whole number ratio of the atoms in the compound. We can use the given masses of carbon, hydrogen, and oxygen to do this.
First, we need to convert the masses of the elements to moles. To do this, we divide the mass of each element by its molar mass:
$\text{moles of C} = 24.0~\mathrm{g}/12.01~\mathrm{g/mol} = 1.999~\mathrm{mol}$
$\text{moles of H} = 3.0~\mathrm{g}/1.008~\mathrm{g/mol} = 2.976~\mathrm{mol}$
$\text{moles of O} = 1.6~\mathrm{g}/16.00~\mathrm{g/mol} = 0.100~\mathrm{mol}$
Next, we divide each of the mole values by the smallest mole value to get the mole ratio of the elements. In this case, the smallest mole value is 0.100 mol, which corresponds to oxygen:
$\text{moles of C} = 1.999~\mathrm{mol}/0.100~\mathrm{mol} = 19.99 \approx 20$
$\text{moles of H} = 2.976~\mathrm{mol}/0.100~\mathrm{mol} = 29.76 \approx 30$
$\text{moles of O} = 0.100~\mathrm{mol}/0.100~\mathrm{mol} = 1$
Finally, we write the empirical formula using the whole number mole ratios as subscripts. The empirical formula is therefore $\mathrm{C}{20}\mathrm{H}{30}\mathrm{O}$.
Therefore, the correct answer is A. $\mathrm{C}_{20}\mathrm{H}_{30}\mathrm{O}$.
Question-3 :2021-may-Chemistry_paper_1__TZ1_HL
Topic:
Calculate: What volume of oxygen, in $\mathrm{dm}^3$ at STP, is needed when $5.8 \mathrm{~g}$ of butane undergoes complete combustion?
$$
2 \mathrm{C}_4 \mathrm{H}_{10}(\mathrm{~g})+13 \mathrm{O}_2(\mathrm{~g}) \rightarrow 8 \mathrm{CO}_2(\mathrm{~g})+10 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$$
A. $2 \times \frac{5.8}{12.01 \times 4+1.01 \times 10} \times 13 \times 22.7$
B. $\frac{5.8}{12.01 \times 4+1.01 \times 10} \times \frac{13}{2} \times 22.7$
C. $\frac{5.8}{12.01 \times 4+1.01 \times 10} \times \frac{2}{13} \times 22.7$
D. $\frac{5.8}{12.01 \times 4+1.01 \times 10} \times \frac{13}{2} \times \frac{22.7}{1000}$
Answer/Explanation
Solution:
First, we need to balance the chemical equation to determine the stoichiometry of the reaction. Here, we have:
$$
2 \mathrm{C}_4 \mathrm{H}_{10}(\mathrm{~g})+13 \mathrm{O}_2(\mathrm{~g}) \rightarrow 8 \mathrm{CO}_2(\mathrm{~g})+10 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$$
This means that 2 moles of butane reacts with 13 moles of oxygen to produce 8 moles of carbon dioxide and 10 moles of water.
This means that 2 moles of butane reacts with 13 moles of oxygen to produce 8 moles of carbon dioxide and 10 moles of water.
Next, we can use stoichiometry to determine the amount of oxygen needed to react with 5.8 g of butane. The molar mass of butane is $12.01 \times 4+1.01 \times 10 = 58.12$ g/mol. Thus, we have:
$$
5.8 \mathrm{~g} \times \frac{1 \mathrm{~mol}}{58.12 \mathrm{~g}} \times \frac{13 \mathrm{~mol} \mathrm{O}_2}{2 \mathrm{~mol} \mathrm{C}_4 \mathrm{H}_{10}}=12.7 \mathrm{~mol} \mathrm{O}_2
$$
Finally, we can use the ideal gas law to determine the volume of oxygen needed at STP $\left(0^{\circ} \mathrm{C}\right.$ and $1 \mathrm{~atm}$ pressure), where 1 mole of any gas occupies $22.7 \mathrm{~L}$ :
$$
V=\frac{n R T}{P}=\frac{12.7 \mathrm{~mol} \times 0.0821(\mathrm{~L} \mathrm{~atm}) /(\mathrm{mol} \mathrm{K}) \times 273 \mathrm{~K}}{1 \mathrm{~atm}} \approx 291 \mathrm{~L}
$$
Converting to dm$^3$ (liters), we have $V = 291 \mathrm{~L} = 291 \mathrm{~dm^3}$.
Therefore, the answer is (B) $\frac{5.8}{12.01 \times 4+1.01 \times 10} \times \frac{13}{2} \times 22.7$.
Question-4 :2021-may-Chemistry_paper_1__TZ1_HL
Topic:
Discuss: What is the relative molecular mass of bromine, according to the following mass spectrum?
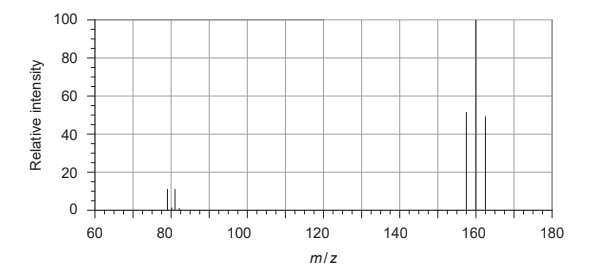
A. $\frac{158 \times 52+160 \times 100+162 \times 48}{52+100+48}$
B. $\frac{158 \times 52+160 \times 100+162 \times 48}{158+160+162}$
C. $\frac{79 \times 11+81 \times 11+158 \times 52+160 \times 100+162 \times 48}{11+11+52+100+48}$
D. $\frac{79 \times 11+81 \times 11}{11+11}$
Answer/Explanation
Solution:
Relative molecular mass of $\mathrm{Br}_ 2=\frac{158 \times 52+160 \times 100+162 \times 48}{(52+100+48)}$
$
\begin{aligned}
& =\frac{8216+16000+7776 }{ 200}\\
& =\frac{31992 }{ 200} \\
& =159.96
\end{aligned}
$
Option $b$ and $c$ are incorrect .Option d will give molecular mass of $\mathrm{Br}$-atom.
$\colorbox{yellow}{Correct Option : A}$
Question-5 :2021-may-Chemistry_paper_1__TZ1_HL
Topic:
Discuss: Which represents a $p$ orbital?
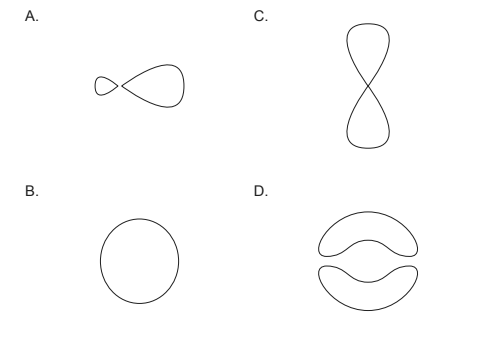
Answer/Explanation
Solution:
A $p$ orbital is one of the three types of orbitals in an atom, the others being s and d orbitals. It has a dumbbell shape and consists of two lobes on either side of the nucleus separated by a node, which is a plane where the probability of finding the electron is zero.
Mathematically, a $p$ orbital is represented by three wave functions, which correspond to the three possible orientations of the dumbbell-shaped orbital along the x, y, and z axes. These wave functions are:
$\begin{aligned} & \psi_{p_x}=\frac{1}{\sqrt{2}}\left(\psi_{+1}-\psi_{-1}\right) \\ & \psi_{p_y}=\frac{1}{\sqrt{2} i}\left(\psi_{+1}+\psi_{-1}\right) \\ & \psi_{p_z}=\psi_0\end{aligned}$
Here, $\psi_{+1}$, $\psi_{-1}$, and $\psi_{0}$ represent the wave functions of the three possible values of the magnetic quantum number (m) for a p orbital: m=1, m=-1, and m=0, respectively. The subscripts $p_x$, $p_y$, and $p_z$ indicate the orientation of the p orbital along the x, y, and z axes, respectively.
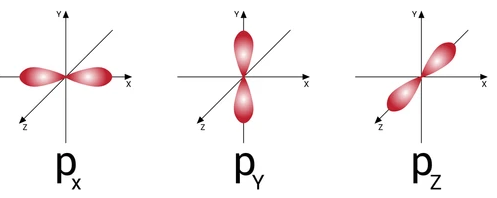
The probability density of finding an electron in a p orbital is proportional to the square of the wave function, and varies with distance from the nucleus and direction relative to the axis of orientation.