Question-1 :2021-may-Chemistry_paper_1__TZ1_SL
Topic:
Discuss: Which contains the most atoms of oxygen?
A. $64 \mathrm{~g}$ of $\mathrm{O}_2$
B. $1.2 \times 10^{24}$ molecules of $\mathrm{O}_2$
C. $64 \mathrm{~g}$ of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$
D. $1.2 \times 10^{24}$ molecules of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$
Answer/Explanation
Solution:
To determine which option contains the most atoms of oxygen, we need to calculate the total number of oxygen atoms in each option.
A. $64 \mathrm{~g}$ of $\mathrm{O}_2$: The molar mass of oxygen is $16 \mathrm{~g/mol}$. Therefore, $64 \mathrm{~g}$ of $\mathrm{O}_2$ contains $64 \mathrm{~g} /16 \mathrm{~g/mol} = 4$ moles of oxygen.
“1 mole of any element contains $6.022 \times 10^{23}$ atoms.”
$\therefore$ no. of atoms in 4 moles $\mathrm{O}_2=4 \times 6.022 \times 10^{23}=2.4088 \times 10^{24}$ atoms.
B. $1.2 \times 10^{24}$ molecules of $\mathrm{O}_2$: $1.2 \times 10^{24}$ molecules of $\mathrm{O}_2$ contain $1.2 \times 10^{24}$ molecules $\times 2$ atoms/molecule $= 2.4 \times 10^{24}$ atoms of oxygen.
C. $64 \mathrm{~g}$ of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$: The molar mass of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$ is $89 \mathrm{~g/mol}$. Therefore, $64 \mathrm{~g}$ of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$
contains $64 \mathrm{~g} / 89 \mathrm{~g/mol} = 0.719 \mathrm{~mol}$ of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$. Each mole of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$ contains $3$ atoms of oxygen, so $64 \mathrm{~g}$ of
$\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$ contains $0.719 \mathrm{~mol} \times 3 \mathrm{~atoms/mol} = 2.157 \mathrm{~mol}$ of oxygen atoms. The total number of oxygen atoms is $2.157 \mathrm{~mol} \times 6.02 \times 10^{23}\mathrm{~atoms/mol} = 1.298 \times 10^{24}$ atoms.
D. $1.2 \times 10^{24}$ molecules of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$: $1.2 \times 10^{24}$ molecules of $\mathrm{C}_3 \mathrm{H}_5 \mathrm{O}_3$ contain $1.2 \times 10^{24}$ molecules $\times 3$ atoms/molecule $= 3.6 \times 10^{24}$ atoms of oxygen.
Therefore, option D contains the most atoms of oxygen.
Question-2 :2021-may-Chemistry_paper_1__TZ1_SL
Topic:
Calculate: What is the resulting concentration, in $\mathrm{mol} \mathrm{dm}^{-3}$, when $1.0 \mathrm{~cm}^3$ of $0.500 \mathrm{~mol} \mathrm{dm}^{-3}$ nitric acid solution is diluted to $50.0 \mathrm{~cm}^3$ with water?
A. $0.002$
B. $0.01$
C. $0.04$
D. $0.1$
Answer/Explanation
Solution:
To solve this problem, we can use the equation:
$C_1V_1 = C_2V_2$
where $C_1$ and $V_1$ are the initial concentration and volume of the solution, and $C_2$ and $V_2$ are the final concentration and volume of the solution.
In this case, we have:
$C_1 = 0.500~\mathrm{mol~dm^{-3}}$
$V_1 = 1.0~\mathrm{cm^3} = 1.0~\mathrm{ml}$
$V_2 = 50.0~\mathrm{cm^3} = 50.0~\mathrm{ml}$
We want to find $C_2$. Substituting the values into the equation, we get:
$0.500~\mathrm{moldm^{-3}} \times 1.0\mathrm{ml} = C_2 \times 50.0~\mathrm{ml}$
Simplifying, we get:
$C_2 = \frac{0.500~\mathrm{moldm^{-3}} \times 1.0\mathrm{ml}}{50.0~\mathrm{ml}} = 0.01~\mathrm{mol~dm^{-3}}$
Therefore, the resulting concentration when $1.0 \mathrm{~cm}^3$ of $0.500 \mathrm{~mol} \mathrm{dm}^{-3}$ nitric acid solution is diluted to $50.0 \mathrm{cm}^3$ with water is 0.01 $\mathrm{moldm^{-3}}$. The correct answer is option B.
Question-3 :2021-may-Chemistry_paper_1__TZ1_SL
Topic:
Calculate: What volume of oxygen, in $\mathrm{dm}^3$ at STP, is needed when $5.8 \mathrm{~g}$ of butane undergoes complete combustion?
$$
2 \mathrm{C}_4 \mathrm{H}_{10}(\mathrm{~g})+13 \mathrm{O}_2(\mathrm{~g}) \rightarrow 8 \mathrm{CO}_2(\mathrm{~g})+10 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$$
A. $2 \times \frac{5.8}{12.01 \times 4+1.01 \times 10} \times 13 \times 22.7$
B. $\frac{5.8}{12.01 \times 4+1.01 \times 10} \times \frac{13}{2} \times 22.7$
C. $\frac{5.8}{12.01 \times 4+1.01 \times 10} \times \frac{2}{13} \times 22.7$
D. $\frac{5.8}{12.01 \times 4+1.01 \times 10} \times \frac{13}{2} \times \frac{22.7}{1000}$
Answer/Explanation
Solution:
First, we need to balance the chemical equation to determine the stoichiometry of the reaction. Here, we have:
$$
2 \mathrm{C}_4 \mathrm{H}_{10}(\mathrm{~g})+13 \mathrm{O}_2(\mathrm{~g}) \rightarrow 8 \mathrm{CO}_2(\mathrm{~g})+10 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$$
This means that 2 moles of butane reacts with 13 moles of oxygen to produce 8 moles of carbon dioxide and 10 moles of water.
This means that 2 moles of butane reacts with 13 moles of oxygen to produce 8 moles of carbon dioxide and 10 moles of water.
Next, we can use stoichiometry to determine the amount of oxygen needed to react with 5.8 g of butane. The molar mass of butane is $12.01 \times 4+1.01 \times 10 = 58.12$ g/mol. Thus, we have:
$$
5.8 \mathrm{~g} \times \frac{1 \mathrm{~mol}}{58.12 \mathrm{~g}} \times \frac{13 \mathrm{~mol} \mathrm{O}_2}{2 \mathrm{~mol} \mathrm{C}_4 \mathrm{H}_{10}}=12.7 \mathrm{~mol} \mathrm{O}_2
$$
Finally, we can use the ideal gas law to determine the volume of oxygen needed at STP $\left(0^{\circ} \mathrm{C}\right.$ and $1 \mathrm{~atm}$ pressure), where 1 mole of any gas occupies $22.7 \mathrm{~L}$ :
$$
V=\frac{n R T}{P}=\frac{12.7 \mathrm{~mol} \times 0.0821(\mathrm{~L} \mathrm{~atm}) /(\mathrm{mol} \mathrm{K}) \times 273 \mathrm{~K}}{1 \mathrm{~atm}} \approx 291 \mathrm{~L}
$$
Converting to dm$^3$ (liters), we have $V = 291 \mathrm{~L} = 291 \mathrm{~dm^3}$.
Therefore, the answer is (B) $\frac{5.8}{12.01 \times 4+1.01 \times 10} \times \frac{13}{2} \times 22.7$.
Question-4 :2021-may-Chemistry_paper_1__TZ1_SL
Topic:
Calculate: What is the coefficient of $\mathrm{HCl}$ (aq) when the equation is balanced using the smallest possible whole numbers?
$$
\ldots \mathrm{CuO}(\mathrm{s})+\ldots \mathrm{HCl}(\mathrm{aq}) \rightarrow \mathrm{CuCl}_2(\mathrm{aq})+\ldots \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$$
A. $1$
B. $2$
C. $3$
D. $4$
Answer/Explanation
Solution:
To balance this chemical equation, we need to ensure that the number of atoms of each element is equal on both the reactant and product sides. Here, we have copper oxide $\mathrm{CuO}$ and hydrochloric acid $\mathrm{HCl}$ on the left side, and copper(II) chloride $\mathrm{CuCl}_2$ and water $\mathrm{H}_2 \mathrm{O}$ on the right side.
The unbalanced equation is:
$\mathrm{CuO}(\mathrm{s}) + \mathrm{HCl}(\mathrm{aq}) \rightarrow \mathrm{CuCl}_2(\mathrm{aq}) + \mathrm{H}_2 \mathrm{O}(\mathrm{l})$
To balance the equation, we can start by balancing the copper atoms on both sides. There is one copper atom on the left side and one copper atom on the right side, so we don’t need to adjust the coefficients for $\mathrm{CuO}$ and $\mathrm{CuCl}_2$.
Next, we can balance the chlorine atoms. There is one chlorine atom on the left side and two chlorine atoms on the right side, so we need to balance the equation by multiplying $\mathrm{HCl}$ by 2:
$\mathrm{CuO}(\mathrm{s}) + 2\mathrm{HCl}(\mathrm{aq}) \rightarrow \mathrm{CuCl}_2(\mathrm{aq}) + \mathrm{H}_2 \mathrm{O}(\mathrm{l})$
Now, we have 2 chlorine atoms on both sides of the equation. Finally, we can balance the hydrogen and oxygen atoms by adding a coefficient of 1 for $\mathrm{H}_2 \mathrm{O}$:
$\mathrm{CuO}(\mathrm{s}) + 2\mathrm{HCl}(\mathrm{aq}) \rightarrow \mathrm{CuCl}_2(\mathrm{aq}) + \mathrm{H}_2 \mathrm{O}(\mathrm{l})$
The balanced equation shows that we need a coefficient of 2 for $\mathrm{HCl}(\mathrm{aq})$. Therefore, the answer is option B, 2.
Question-5 :2021-may-Chemistry_paper_1__TZ1_SL
Topic:
Discuss: What is the relative molecular mass of bromine, according to the following mass spectrum?
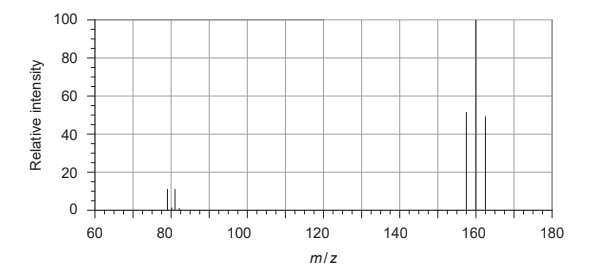
A. $\frac{158 \times 52+160 \times 100+162 \times 48}{52+100+48}$
B. $\frac{158 \times 52+160 \times 100+162 \times 48}{158+160+162}$
C. $\frac{79 \times 11+81 \times 11+158 \times 52+160 \times 100+162 \times 48}{11+11+52+100+48}$
D. $\frac{79 \times 11+81 \times 11}{11+11}$
Answer/Explanation
Solution:
Relative molecular mass of $\mathrm{Br}_ 2=\frac{158 \times 52+160 \times 100+162 \times 48}{(52+100+48)}$
$
\begin{aligned}
& =\frac{8216+16000+7776 }{ 200}\\
& =\frac{31992 }{ 200} \\
& =159.96
\end{aligned}
$
Option $b$ and $c$ are incorrect .Option d will give molecular mass of $\mathrm{Br}$-atom.