Question-1 (a):2021-may-Chemistry_paper_2__TZ2_HL
Topic:
Given: Limestone can be converted into a variety of useful commercial products through the lime cycle. Limestone contains high percentages of calcium carbonate, $\mathrm{CaCO}_3$.
Calcium carbonate is heated to produce calcium oxide, $\mathrm{CaO}$.
$$
\mathrm{CaCO}_3(\mathrm{~s}) \rightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})
$$
Calculate: the volume of carbon dioxide produced at STP when $555 \mathrm{~g}$ of calcium carbonate decomposes. Use sections 2 and 6 of the data booklet.
Answer/Explanation
Solution:
The balanced chemical equation for the decomposition of calcium carbonate is:
$$\mathrm{CaCO}_3(\mathrm{~s}) \rightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})$$
From the equation, we can see that 1 mole of calcium carbonate produces 1 mole of carbon dioxide. The molar mass of calcium carbonate is $100.09 \mathrm{~g/mol}$, so $555 \mathrm{~g}$ of calcium carbonate is equal to:
$$
\frac{555\mathrm{~g}}{100.09\mathrm{~g/mol}}=5.549\mathrm{~mol}
$$
Therefore, we can expect to produce 5.549 moles of carbon dioxide at STP. According to section 6 of the data booklet, STP (standard temperature and pressure) is defined as $273.15\mathrm{~K}$ and $10^5\mathrm{~Pa}$.
Using the ideal gas law (section 2 of the data booklet), we can calculate the volume of carbon dioxide produced:
$$
V = \frac{nRT}{P}
$$
where $n$ is the number of moles of gas, $R$ is the gas constant ($8.31\mathrm{~J/(mol~K)}$), $T$ is the temperature in Kelvin, and $P$ is the pressure in Pascals.
Substituting the values, we get:
$$
V = \frac{5.549\mathrm{~mol} \times 8.31\mathrm{~J/(mol~K)} \times 273.15\mathrm{~K}}{10^5\mathrm{~Pa}} \approx 125.98 \mathrm{~L}
$$
Therefore, the volume of carbon dioxide produced at STP when $555 \mathrm{~g}$ of calcium carbonate decomposes is approximately $125.98 \mathrm{~L}/\mathrm{dm^3}$.
Question-1[(b) (i)]:2021-may-Chemistry_paper_2__TZ2_HL
Topic:
Given: Thermodynamic data for the decomposition of calcium carbonate is given.
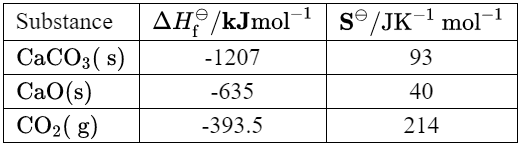
Calculate: the enthalpy change of reaction, $\Delta H$, in $\mathrm{kJ}$, for the decomposition of calcium carbonate.
Answer/Explanation
Solution:
The enthalpy change of reaction ($\Delta H$) for the decomposition of calcium carbonate can be calculated using the standard enthalpies of formation of the reactants and products, according to the following equation:
$$\Delta H = \sum\Delta H_{\mathrm{f}}^{\ominus}(\mathrm{products}) – \sum\Delta H_{\mathrm{f}}^{\ominus}(\mathrm{reactants})$$
where $\Delta H_{\mathrm{f}}^{\ominus}$ is the standard enthalpy of formation of the substance.
From the balanced chemical equation:
$$\mathrm{CaCO}_3(\mathrm{~s}) \rightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})$$
the reaction produces 1 mole of $\mathrm{CaO}$ and 1 mole of $\mathrm{CO}_2$ for every mole of $\mathrm{CaCO}_3$ decomposed.
Using the data from the table, we can calculate the enthalpy change of reaction as follows:
\begin{align*}
\Delta H &= \Delta H_{\mathrm{f}}^{\ominus}(\mathrm{CaO}) + \Delta H_{\mathrm{f}}^{\ominus}(\mathrm{CO}_2) – \Delta H_{\mathrm{f}}^{\ominus}(\mathrm{CaCO}_3) \\
&= (-635\mathrm{~kJ/mol}) + (-393.5\mathrm{~kJ/mol}) – (-1207\mathrm{~kJ/mol}) \\
&= 178.5\mathrm{~kJ/mol}
\end{align*}
Therefore, the enthalpy change of reaction for the decomposition of calcium carbonate is $178.5 \mathrm{~kJ/mol}$.
Question-1[(b) (ii)]:2021-may-Chemistry_paper_2__TZ2_HL
Topic:
Calculate: the change in entropy, $\Delta S$, in $\mathrm{J} \mathrm{K}^{-1}$, for the decomposition of calcium carbonate.
Answer/Explanation
Solution:
The change in entropy ($\Delta S$) for the decomposition of calcium carbonate can be calculated using the standard entropies of the reactants and products, according to the following equation:
$$\Delta S = \sum S^{\ominus}(\mathrm{products}) – \sum S^{\ominus}(\mathrm{reactants})$$
where $S^{\ominus}$ is the standard entropy of the substance.
From the balanced chemical equation:
$$\mathrm{CaCO}_3(\mathrm{~s}) \rightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})$$
the reaction produces 1 mole of $\mathrm{CaO}$ and 1 mole of $\mathrm{CO}_2$ for every mole of $\mathrm{CaCO}_3$ decomposed.
Using the data from the table, we can calculate the change in entropy as follows:
\begin{align*}
\Delta S &= S^{\ominus}(\mathrm{CaO}) + S^{\ominus}(\mathrm{CO}_2) – S^{\ominus}(\mathrm{CaCO}_3) \\
&= (40\mathrm{~J/(K\cdot mol)}) + (214\mathrm{~J/(K\cdot mol)}) – (93\mathrm{~J/(K\cdot mol)}) \\
&= 161\mathrm{~J/(K\cdot mol)}
\end{align*}
Therefore, the change in entropy for the decomposition of calcium carbonate is $161 \mathrm{~J/(K\cdot mol)}$.
Question-1[(b) (iii)]:2021-may-Chemistry_paper_2__TZ2_HL
Topic:
Determine: the temperature, in $\mathrm{K}$, at which the decomposition of calcium carbonate becomes spontaneous, using b(i), b(ii) and section 1 of the data booklet.
(If you do not have answers for $b$ (i) and b(ii), use $\Delta H=190 \mathrm{~kJ}$ and $\Delta S=180 \mathrm{JK}^{-1}$, but these are not the correct answers.)
Answer/Explanation
Solution:
The Gibbs free energy change ($\Delta G$) for the reaction can be calculated using the following equation:
$$\Delta G = \Delta H – T\Delta S$$
where $\Delta H$ is the enthalpy change of reaction, $\Delta S$ is the change in entropy, and $T$ is the temperature in Kelvin.
For the reaction to be spontaneous, $\Delta G$ must be negative. Thus, we can rearrange the above equation to solve for the temperature at which $\Delta G$ becomes zero:
$$T_{\mathrm{spont}} = \frac{\Delta H}{\Delta S}$$
Using the values calculated in parts (i) and (ii), we can calculate the temperature at which the decomposition of calcium carbonate becomes spontaneous as follows:
$$T_{\mathrm{spont}} = \frac{178.5\mathrm{~kJ/mol}}{161\mathrm{~J/(K\cdot mol)}} = 1108\mathrm{~K}$$
Therefore, the decomposition of calcium carbonate becomes spontaneous at a temperature of $1108\mathrm{~K}$.
Question-1[(b) (iv)]:2021-may-Chemistry_paper_2__TZ2_HL
Topic:
Sketch: an energy profile for the decomposition of calcium carbonate based on your answer to $b(i)$, labelling the axes and activation energy, $E_a$.
Answer/Explanation
Solution:
The energy profile for the decomposition of calcium carbonate can be sketched based on the enthalpy change of reaction calculated in part (i). The reaction is an endothermic process, meaning that it absorbs heat and energy from the surroundings. The energy profile can be sketched as follows:
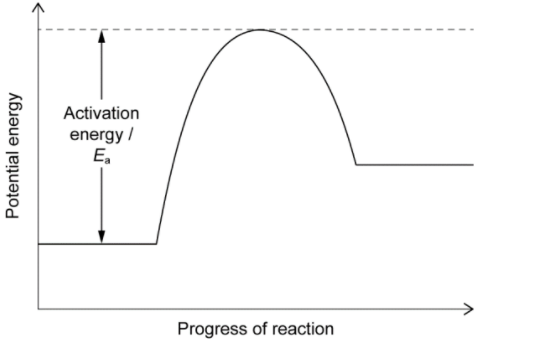
The vertical axis represents the energy of the reaction, and the horizontal axis represents the progress of the reaction. The energy of the reactants, $\mathrm{CaCO}_3$, is shown at the beginning of the reaction, and the energy of the products, $\mathrm{CaO}$ and $\mathrm{CO}_2$, is shown at the end of the reaction.
The activation energy, $E_a$, represents the minimum amount of energy required for the reaction to proceed. It can be estimated by the height of the energy barrier between the reactants and products. In this case, the activation energy can be estimated to be the difference in enthalpy between the reactants and the transition state, which is not shown in the energy profile. The activation energy can be calculated as follows:
$$E_a = \Delta H_{\mathrm{f}}^{\ominus}(\mathrm{CaO}) – \Delta H_{\mathrm{f}}^{\ominus}(\mathrm{CaCO}_3) = (-635\mathrm{~kJ/mol}) – (-1207\mathrm{~kJ/mol}) = 572\mathrm{~kJ/mol}$$
Therefore, the activation energy for the decomposition of calcium carbonate is approximately $572\mathrm{~kJ/mol}$.
Question-1[(b) (v)]:2021-may-Chemistry_paper_2__TZ2_HL
Topic:
Discuss: how adding a catalyst to the reaction would impact the enthalpy change of reaction, $\Delta H$, and the activation energy, $E_a$.
$\Delta H$:……………………………………………..
$E_{\mathrm{a}}$:………………………………..
Answer/Explanation
Solution:
Adding a catalyst to the reaction would not impact the enthalpy change of reaction, $\Delta H$. This is because a catalyst does not participate in the reaction as a reactant or a product, and therefore it does not affect the energy difference between the reactants and products.
However, adding a catalyst would decrease the activation energy, $E_a$, for the reaction. A catalyst works by providing an alternative reaction pathway with a lower activation energy than the uncatalyzed reaction. This lower activation energy allows more reactant molecules to have enough energy to overcome the energy barrier and react, increasing the rate of the reaction.
Therefore, adding a catalyst would decrease the activation energy, $E_a$, for the decomposition of calcium carbonate, making the reaction proceed more quickly.