Question-1 :2021-nov-Chemistry_paper_1__TZ0_HL
Topic:
Given: Avogadro’s constant, $L$ or $N_A: 6.02 \times 10^{23} \mathrm{~mol}^{-1}$
Calculate: How much ethanol contains $1.20 \times 10^{24}$ atoms of carbon?
A. $0.333 \mathrm{~mol}$
B. $0.500 \mathrm{~mol}$
C. $1.00 \mathrm{~mol}$
D. $2.00 \mathrm{~mol}$
Answer/Explanation
Solution:
Number of moles of carbon = $1.20 \times 10^{24} \text{ atoms} \times \frac{1 \text{ mol}}{6.02 \times 10^{23} \text{ atoms}} = 1.99 \text{ mol}$
Since there are two carbon atoms in each molecule of ethanol, the number of moles of ethanol is half of the number of moles of carbon:
Number of moles of ethanol = $\frac{1}{2} \times 1.99 \text{ mol} = 0.995 \text{ mol}$
Therefore, the answer is closest to option C, which is $1.00 \mathrm{~mol}$.
Question-2 :2021-nov-Chemistry_paper_1__TZ0_HL
Topic:
Given: $3.00 \mathrm{~mol}$ of $\mathrm{C}_3 \mathrm{H}_8$ is mixed with $20.00 \mathrm{~mol}$ of $\mathrm{O}_2$.
Discuss: Which quantity is present at the end of the reaction?
$$
\mathrm{C}_3 \mathrm{H}_8(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \rightarrow 3 \mathrm{CO}_2(\mathrm{~g})+4 \mathrm{H}_2 \mathrm{O}(\mathrm{g})
$$
A. $1.00 \mathrm{~mol}$ of $\mathrm{C}_3 \mathrm{H}_8$
B. $5.00 \mathrm{~mol}$ of $\mathrm{O}_2$
C. $12.00 \mathrm{~mol}$ of $\mathrm{CO}_2$
D. $16.00 \mathrm{~mol}$ of $\mathrm{H}_2 \mathrm{O}$
Answer/Explanation
Solution:
The answer is (B) $5.00\ \mathrm{mol}$ of $\mathrm{O}_2$.
To see why, we can use the same method as before to determine the limiting reagent. However, instead of calculating the amount of product produced, we can calculate the amount of reactant consumed.
For $\mathrm{C}_3 \mathrm{H}_8$:
1 mol of $\mathrm{C}_3 \mathrm{H}_8$ reacts with 5 mol of $\mathrm{O}_2$
So, 3.00 mol of $\mathrm{C}_3 \mathrm{H}_8$ would require 15.00 mol of $\mathrm{O}_2$.
For $\mathrm{O}_2$:
5 mol of $\mathrm{O}_2$ reacts with 1 mol of $\mathrm{C}_3 \mathrm{H}_8$
So, 20.00 mol of $\mathrm{O}_2$ would react with 4.00 mol of $\mathrm{C}_3 \mathrm{H}_8$.
Since $\mathrm{O}_2$ requires more $\mathrm{C}_3 \mathrm{H}_8$ than is available, $\mathrm{O}_2$ is in excess and $\mathrm{C}_3 \mathrm{H}_8$ is the limiting reagent. Therefore, the quantity of $\mathrm{O}_2$ present at the end of the reaction is the same as the quantity present at the beginning, which is $20.00\ \mathrm{mol}$.
Question-3 :2021-nov-Chemistry_paper_1__TZ0_HL
Topic:
Given: The two containers shown are connected by a valve.
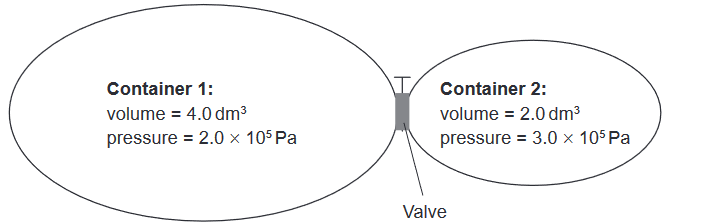
Calculate: What is the total pressure after the valve is opened and the two gas samples are allowed to mix at constant temperature?
A. $1.5 \times 10^5 \mathrm{~Pa}$
B. $2.3 \times 10^5 \mathrm{~Pa}$
C. $2.5 \times 10^5 \mathrm{~Pa}$
D. $5.0 \times 10^5 \mathrm{~Pa}$
Answer/Explanation
Solution:
To solve this problem, we can use the ideal gas law, which states that:
$PV = nRT$
where $P$ is the pressure, $V$ is the volume, $n$ is the number of moles, $R$ is the gas constant, and $T$ is the temperature.
Assuming the temperature is constant and the two gases are ideal, we can combine the two containers and treat them as a single system. The total volume is the sum of the two volumes, or $6.0\ \mathrm{dm^3}$. The total number of moles of gas is not given, but it is not necessary to know it since we only need to calculate the total pressure. Therefore, we can write:
$P_{\mathrm{total}}V_{\mathrm{total}} = (n_1 + n_2)RT$
where $P_{\mathrm{total}}$ is the total pressure, $V_{\mathrm{total}}$ is the total volume, $n_1$ and $n_2$ are the number of moles in containers 1 and 2, respectively, and $R$ and $T$ are constants.
We can rearrange this equation to solve for $P_{\mathrm{total}}$:
$P_{\mathrm{total}} = \frac{(n_1 + n_2)RT}{V_{\mathrm{total}}}$
We don’t know $n_1$ and $n_2$, but we can use the ideal gas law to calculate them separately for each container:
$n_1 = \frac{P_1V_1}{RT}$
$n_2 = \frac{P_2V_2}{RT}$
Substituting these expressions into the first equation, we get:
$P_{\mathrm{total}} = \frac{(P_1V_1 + P_2V_2)}{V_{\mathrm{total}}}$
Substituting the given values, we get:
$P_{\mathrm{total}} = \frac{(2.0 \times 10^5\ \mathrm{Pa} \times 4.0\ \mathrm{dm^3}) + (3.0 \times 10^5\ \mathrm{Pa} \times 2.0\ \mathrm{dm^3})}{6.0\ \mathrm{dm^3}}$
Simplifying, we get:
$P_{\mathrm{total}} = \frac{8.0 \times 10^5\ \mathrm{Pa\cdot dm^3} + 6.0 \times 10^5\ \mathrm{Pa\cdot dm^3}}{6.0\ \mathrm{dm^3}}$
$P_{\mathrm{total}} = \frac{14.0 \times 10^5\ \mathrm{Pa\cdot dm^3}}{6.0\ \mathrm{dm^3}}$
$P_{\mathrm{total}} = 2.3 \times 10^5\ \mathrm{Pa}$
Therefore, the answer is (B) $2.3 \times 10^5\ \mathrm{Pa}$.
Question-4 :2021-nov-Chemistry_paper_1__TZ0_HL
Topic:
Discuss: Which species has two more neutrons than electrons?
$$
\begin{array}{llll}
{ }_3^6 \mathrm{Li}^{+} & { }_4^9 \mathrm{Be}^{2+} & { }_{11}^{23} \mathrm{Na}^{+} & { }_{20}^{42} \mathrm{Ca}^{2+}
\end{array}
$$
A. ${ }_3^6 \mathrm{Li}^{+}$
B. ${ }_4^9 \mathrm{Be}^{2+}$
C. ${ }_{11}^{23} \mathrm{Na}^{+}$
D. ${ }_{20}^{42} \mathrm{Ca}^{2+}$
Answer/Explanation
Solution:
In a neutral atom, the number of electrons is equal to the number of protons. In an ion, the number of electrons is different from the number of protons depending on the charge of the ion. However, the number of neutrons is not related to the charge of the ion.
To determine which species has two more neutrons than electrons, we need to find the number of electrons and the number of neutrons for each species and compare them.
Species A: ${ }_3^6 \mathrm{Li}^{+}$ Number of electrons $= 3-1=2$ Number of neutrons $= 6 – 3 = 3$ Difference between number of neutrons and electrons $= 3 – 3 = 0$
Species B: ${ }_4^9 \mathrm{Be}^{2+}$ Number of electrons $= 4 – 2 = 2$ Number of neutrons $= 9 – 4 = 5$ Difference between number of neutrons and electrons $= 5 – 2 = 3$
Species C: ${ }_{11}^{23} \mathrm{Na}^{+}$ Number of electrons $= 11 – 1 = 10$ Number of neutrons $= 23 – 11 = 12$ Difference between number of neutrons and electrons $= 12 – 10 = 2$
Species D: ${ }_{20}^{42} \mathrm{Ca}^{2+}$ Number of electrons $= 20 – 2 = 18$ Number of neutrons $= 42 – 20 = 22$ Difference between number of neutrons and electrons $= 22 – 18 = 4$
Therefore, the species that has two more neutrons than electrons is species C, ${ }_{11}^{23} \mathrm{Na}^{+}$, so the answer is C.
Question-5 :2021-nov-Chemistry_paper_1__TZ0_HL
Topic:
Discuss: Which statement explains why the second ionization energy of aluminium is higher than the first ionization energy of magnesium?
A. Ionization energy increases along period $3$ .
B. $ p$ electrons are at a higher energy level than $3s$ electrons.
C. $3p$ electrons are further away from the nucleus than $2 p$ electrons.
D. Both have the same number of electrons and aluminium has one more proton.
Answer/Explanation
Solution:
The first ionization energy (IE) is the energy required to remove the first electron from a neutral atom, while the second ionization energy is the energy required to remove the second electron.
To compare the second ionization energy of aluminum and the first ionization energy of magnesium, we need to consider their electron configurations:
- Aluminum: $\mathrm{1s^2 2s^2 2p^6 3s^2 3p^1}$
- Magnesium: $\mathrm{1s^2 2s^2 2p^6 3s^2}$
The first ionization energy of magnesium is lower than the second ionization energy of aluminum because:
A. Ionization energy increases along period 3. This is true, but it doesn’t explain why the second ionization energy of aluminum is higher than the first ionization energy of magnesium.
B. $3p$ electrons are at a higher energy level than $3s$ electrons. This is also true, but it doesn’t explain the difference between the second ionization energy of aluminum and the first ionization energy of magnesium.
C. $3p$ electrons are further away from the nucleus than $2p$ electrons. This is not true. The $3p$ electrons in aluminum are closer to the nucleus than the $2p$ electrons in magnesium.
D. Both have the same number of electrons and aluminum has one more proton. This is also true, but it doesn’t explain why the second ionization energy of aluminum is higher than the first ionization energy of magnesium.
The correct answer is B. The $3p$ electrons in aluminum are at a higher energy level than the $3s$ electrons, and therefore more tightly bound to the nucleus. This means that it takes more energy to remove the $3p$ electron in aluminum than the $3s$ electron in magnesium. As a result, the second ionization energy of aluminum is higher than the first ionization energy of magnesium.