Question-1 :2021-nov-Chemistry_paper_1__TZ0_SL
Topic:
Discuss: What is the number of hydrogen atoms in 2.00 moles of $\mathrm{Ca}\left(\mathrm{HCO}_3\right)_2$ ?
Given: Avogadro’s constant, $L$ or $N_A: 6.02 \times 10^{23} \mathrm{~mol}^{-1}$
A. $2.00$
B. $4.00$
C. $1.20 \times 10^{24}$
D. $2.41 \times 10^{24}$
Answer/Explanation
Solution:
Number of moles of $\mathrm{Ca}\left(\mathrm{HCO}_3\right)_2$=2$
so , no of molecules in it $= 2 \mathrm{N}_a}$
Since there are two hydrogen atoms in each molecule of $\mathrm{Ca}\left(\mathrm{HCO}_3\right)_2$,
Number of hydrogen atoms $\begin{aligned} & =2 \times N_a \times 2 \\ & =4 N_a \\ & =4 \times 6.02 \times 10^{23} \\ & =2.41 \times 10^{24}\end{aligned}$
$\colorbox{yellow}{Correct Option: D}$
Question-2 :2021-nov-Chemistry_paper_1__TZ0_SL
Topic:
Discuss: Which statement describes all homogeneous mixtures?
A. Any sample has the same ratio of the components.
B. The components are covalently bonded together.
C. The components cannot be easily separated.
D. The mixture needs a specific ratio of components to form.
Answer/Explanation
Solution:
Ans: A. Any sample has the same ratio of the components.
This is because in a homogeneous mixture, the components are uniformly distributed throughout the mixture. Therefore, any sample taken from the mixture will have the same ratio of the components.
Option B is incorrect because covalent bonding refers to the sharing of electrons between atoms to form a molecule. A homogeneous mixture can be made up of covalent compounds, but not all of them are covalently bonded.
Option C is partially correct as the components of a homogeneous mixture cannot be easily separated by simple physical means such as filtration, but they can be separated by other methods such as distillation or chromatography.
Option D is incorrect because a homogeneous mixture can have a range of ratios of components and still be homogeneous.
Question-3 :2021-nov-Chemistry_paper_1__TZ0_SL
Topic:
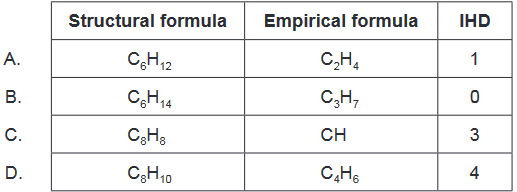
Discuss: Which combination is correct?
Answer/Explanation
Solution:
The correct combination is:
Empirical formula: $\mathrm{C}_3\mathrm{H}_7$
Structural formula: $\mathrm{C}6\mathrm{H}{14}$
IHD: 0
This is option B.
Option A is incorrect because the empirical formula $\mathrm{C}_2\mathrm{H}_4$ corresponds to an alkene with one double bond and therefore an IHD of 1, while the structural formula $\mathrm{C}6\mathrm{H}{12}$ corresponds to a cycloalkane with no double bonds and therefore an IHD of 0.
Option C is incorrect because the empirical formula $\mathrm{CH}$ corresponds to a radical or a carbene, while the structural formula $\mathrm{C}_8\mathrm{H}_8$ corresponds to a substituted cyclooctatetraene with three double bonds and therefore an IHD of 3.
Option D is incorrect because the empirical formula $\mathrm{C}_4\mathrm{H}_6$ corresponds to an alkene with one double bond and therefore an IHD of 1, while the structural formula $\mathrm{C}8\mathrm{H}{10}$ corresponds to a substituted cyclooctatetraene with four double bonds and therefore an IHD of 4.
Question-4 :2021-nov-Chemistry_paper_1__TZ0_SL
Topic:
Given: The two containers shown are connected by a valve.
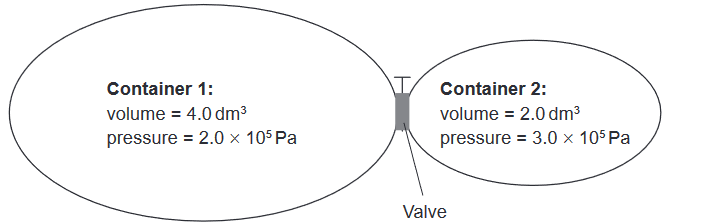
Discuss:What is the total pressure after the valve is opened and the two gas samples are allowed to mix at constant temperature?
A. $1.5 \times 10^5 \mathrm{~Pa}$
B. $2.3 \times 10^5 \mathrm{~Pa}$
C. $2.5 \times 10^5 \mathrm{~Pa}$
D. $5.0 \times 10^5 \mathrm{~Pa}$
Answer/Explanation
Solution:
To solve this problem, we can use the ideal gas law, which states that:
$PV = nRT$
where $P$ is the pressure, $V$ is the volume, $n$ is the number of moles, $R$ is the gas constant, and $T$ is the temperature.
Assuming the temperature is constant and the two gases are ideal, we can combine the two containers and treat them as a single system. The total volume is the sum of the two volumes, or $6.0\ \mathrm{dm^3}$. The total number of moles of gas is not given, but it is not necessary to know it since we only need to calculate the total pressure. Therefore, we can write:
$P_{\mathrm{total}}V_{\mathrm{total}} = (n_1 + n_2)RT$
where $P_{\mathrm{total}}$ is the total pressure, $V_{\mathrm{total}}$ is the total volume, $n_1$ and $n_2$ are the number of moles in containers 1 and 2, respectively, and $R$ and $T$ are constants.
We can rearrange this equation to solve for $P_{\mathrm{total}}$:
$P_{\mathrm{total}} = \frac{(n_1 + n_2)RT}{V_{\mathrm{total}}}$
We don’t know $n_1$ and $n_2$, but we can use the ideal gas law to calculate them separately for each container:
$n_1 = \frac{P_1V_1}{RT}$
$n_2 = \frac{P_2V_2}{RT}$
Substituting these expressions into the first equation, we get:
$P_{\mathrm{total}} = \frac{(P_1V_1 + P_2V_2)}{V_{\mathrm{total}}}$
Substituting the given values, we get:
$P_{\mathrm{total}} = \frac{(2.0 \times 10^5\ \mathrm{Pa} \times 4.0\ \mathrm{dm^3}) + (3.0 \times 10^5\ \mathrm{Pa} \times 2.0\ \mathrm{dm^3})}{6.0\ \mathrm{dm^3}}$
Simplifying, we get:
$P_{\mathrm{total}} = \frac{8.0 \times 10^5\ \mathrm{Pa\cdot dm^3} + 6.0 \times 10^5\ \mathrm{Pa\cdot dm^3}}{6.0\ \mathrm{dm^3}}$
$P_{\mathrm{total}} = \frac{14.0 \times 10^5\ \mathrm{Pa\cdot dm^3}}{6.0\ \mathrm{dm^3}}$
$P_{\mathrm{total}} = 2.3 \times 10^5\ \mathrm{Pa}$
Therefore, the answer is (B) $2.3 \times 10^5\ \mathrm{Pa}$.
Question-5 :2021-nov-Chemistry_paper_1__TZ0_SL
Topic:
Given: Consider the mass spectrum of an element:
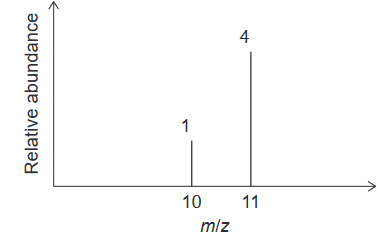
Calculate: What is the relative atomic mass of this element?
A. $10.2$
B. $10.5$
C. $10.8$
D. $10.9$
Answer/Explanation
Solution:
The relative atomic mass of an element can be determined from its mass spectrum by identifying the isotopes present and their relative abundances.
Isotopes are atoms of the same element that have the same number of protons but different numbers of neutrons. These isotopes will appear as peaks in the mass spectrum at different mass-to-charge ratios (m/z).
The relative abundance of each isotope is represented by the area under the peak in the mass spectrum. The relative atomic mass of the element can then be calculated using the formula:
The relative atomic mass
$$
\begin{aligned}
& \\
& = \frac{\left[\text { atomic mass of }{ }^{10} \mathrm{X} \times \text { abundance of }{ }^{10} \mathrm{X}\right]+\left[\text { atomic mass of }{ }^{11} \mathrm{X} \times \text { abundance of }{ }^{11} \mathrm{X}\right.}{\text { abundance of }{ }^{10} \mathrm{X}+\text { abundance of }{ }^{11} \mathrm{X}} \\
& =\frac{[10 \times1]+[11 \times 4]}{1+4}=10.8 \mathrm{amu}
\end{aligned}
$$