Q.1(a).2021-May-Physics_paper_2__TZ1_SL
Topic: Motion
Given: Two players are playing table tennis. Player $A$ hits the ball at a height of $0.24 \mathrm{~m}$ above the edge of the table, measured from the top of the table to the bottom of the ball. The initial speed of the ball is $12.0 \mathrm{~ms}^{-1}$ horizontally. Assume that air resistance is negligible.
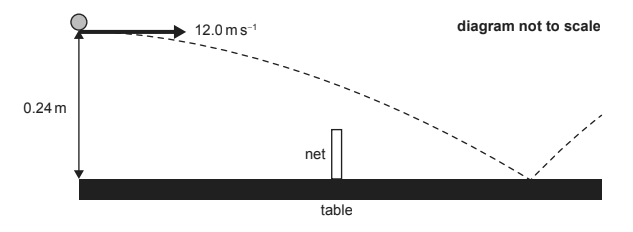
Show that: the time taken for the ball to reach the surface of the table is about $0.2 \mathrm{~s}$.
Answer/Explanation
Solution:
We can solve this problem using kinematic equations. The motion of the ball can be divided into two parts: horizontal motion with constant velocity and vertical motion under constant acceleration due to gravity.
The initial vertical velocity of the ball is zero, and the acceleration due to gravity is $g = 9.8 \mathrm{~ms}^{-2}$ downwards. We can use the following kinematic equation to find the time taken for the ball to reach the surface of the table:
$$
y=y_0+v_{0, y} t+\frac{1}{2} a_y t^2
$$
where $y$ is the final vertical position of the ball (equal to the height of the table), $y_0$ is the initial vertical position of the ball (equal to the height above the table), $v_{0,y}$ is the initial vertical velocity of the ball (zero in this case), $a_y$ is the vertical acceleration of the ball due to gravity, and $t$ is the time taken for the ball to reach the table.
Substituting the given values, we have:
$$
0.24 \mathrm{~m}=0+0 \times t+\frac{1}{2} \times 9.8 \mathrm{~ms}^{-2} \times t^2
$$
Simplifying and solving for $t$, we get:
$$
\colorbox{yellow}{$t=\sqrt{\frac{2 \times 0.24 \mathrm{~m}}{9.8 \mathrm{~ms}^{-2}}} \approx 0.2 \mathrm{~s}$}
$$
Therefore, the time taken for the ball to reach the surface of the table is about $0.2 \mathrm{~s}$.
Q.1(b).2021-May-Physics_paper_2__TZ1_SL
Topic: Motion
Sketch: on the axes, a graph showing the variation with time of the vertical component of velocity $v_v$ of the ball until it reaches the table surface. Take $g$ to be $+10 \mathrm{~ms}^{-2}$.
Answer/Explanation
Solution:
To sketch the graph of the vertical component of velocity $v_v$ of the ball as a function of time, we can use the kinematic equation:
$$
v_y=v_{0, y}+a_y t
$$
where $v_y$ is the vertical velocity of the ball at time $t$, $v_{0,y}$ is the initial vertical velocity of the ball (zero in this case), $a_y$ is the vertical acceleration due to gravity, and $t$ is the time elapsed since the ball was hit.
Substituting $a_y = +10 \mathrm{~ms}^{-2}$ (since $g$ is positive in the upward direction), we get:
$$
v_y=0+10 \mathrm{~ms}^{-2} t
$$
This is a straight line with a positive slope of $9.8 \mathrm{~ms}^{-2}$, passing through the origin. The graph of $v_v$ versus $t$ will look like this:
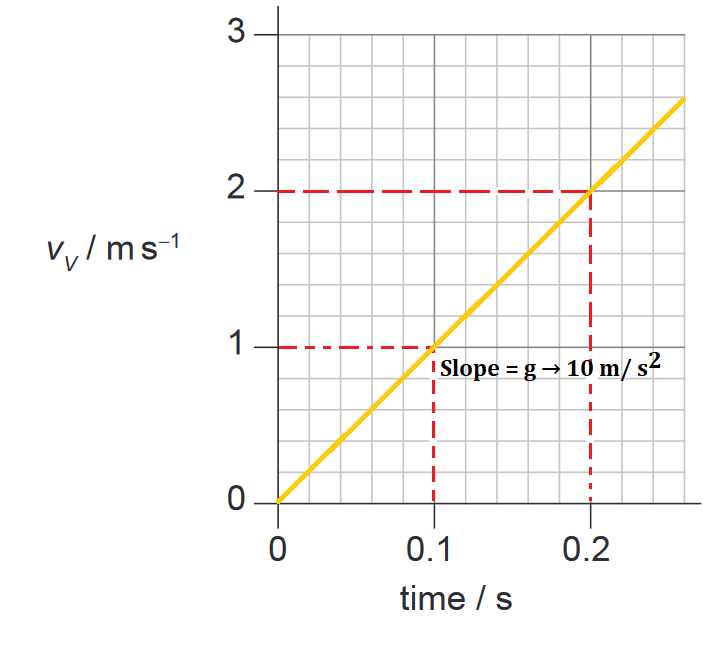
Q.1(c).2021-May-Physics_paper_2__TZ1_SL
Topic: Motion
Given: The net is stretched across the middle of the table. The table has a length of $2.74 \mathrm{~m}$ and the net has a height of $15.0 \mathrm{~cm}$.
Show that: the ball will go over the net.
Answer/Explanation
Solution:
Q.1[(d) (i)].2021-May-Physics_paper_2__TZ1_SL
Topic: Work, energy and power
Given: The ball bounces and then reaches a peak height of $0.18 \mathrm{~m}$ above the table with a horizontal speed of $10.5 \mathrm{~m} \mathrm{~s}^{-1}$. The mass of the ball is $2.7 \mathrm{~g}$.
Calculate: the kinetic energy of the ball immediately after the bounce.
Answer/Explanation
Solution:
We can use the conservation of energy to determine the vertical component of the velocity of the ball when it reaches a peak height of $0.18 \mathrm{~m}$ above the table.
At the peak height, the ball’s kinetic energy is zero since it has come to a momentary stop, so all of the energy is in the form of potential energy due to gravity. Using the conservation of energy equation:
$$
P E_{\text {initial }}+K E_{\text {initial }}=P E_{\text {final }}+K E_{\text {final }}
$$
where $PE$ is the potential energy due to gravity and $KE$ is the kinetic energy, we can solve for the final vertical velocity $v_{y,\mathrm{final}}$:
$$
m g h_{\text {final }}=\frac{1}{2} m v_{\text {final }}^2 \Longrightarrow v_{y, \text { final }}=\sqrt{2 g h_{\text {final }}}
$$
where $m$ is the mass of the ball, $g$ is the acceleration due to gravity, $h_{\mathrm{final}}$ is the peak height of the ball above the table, and we have used the fact that the horizontal component of the velocity does not affect the vertical motion.
Substituting the given values, we get:
$$
v_{y, \text { final }}=\sqrt{2 \times 10 \mathrm{~m} \mathrm{~s}^{-2} \times 0.18 \mathrm{~m}} \approx 1.88 \mathrm{~m} \mathrm{~s}^{-1}
$$
$$
v_{x, \text { final }}= 10.5 \mathrm{~m} \mathrm{~s}^{-1}\quad\text{(given)}
$$
$$
v=\sqrt{10.5^2+1.88^2} =10.67 \mathrm{ms}^{-1}
$$
Using the formula for kinetic energy, $KE = \frac{1}{2}mv^2$, where $m$ is the mass of the ball and $v$ is its speed, we can calculate the kinetic energy of the ball immediately after the bounce:
$$
\colorbox{yellow}{$\mathrm{KE}=\frac{1}{2} \times 0.0027 \times 10.67^2 \approx 0.15 \mathrm{~J}$}
$$
Q.1[(d) (ii].2021-May-Physics_paper_2__TZ1_SL
Topic: Momentum and impulse
Given: Player B intercepts the ball when it is at its peak height. Player B holds a paddle (racket) stationary and vertical. The ball is in contact with the paddle for $0.010 \mathrm{~s}$. Assume the collision is elastic.

Calculate: the average force exerted by the ball on the paddle. State your answer to an appropriate number of significant figures.
Answer/Explanation
Solution:
we can use the definition of average force $F_{\mathrm{avg}} = \frac{\Delta p}{\Delta t}$, where $\Delta p$ is the change in momentum of the ball and $\Delta t$ is the duration of the collision.
After the collision, the ball rebounds with the same speed and direction but with a momentum of $p_{\mathrm{final}} = -mv$, where the negative sign indicates a reversal of the direction of the momentum due to the collision with the paddle. [$\text{Right direction} \rightarrow \text{positive}$]
The change in momentum of the ball is:
$$
\Delta p=p_{\text {final }}-p_{\text {initial }}=(m v)-(-m v)=2 m v\quad\text{(v= 10.5 m/s )}
$$
$2mv=2\times 0.0027\times 10.5=0.0567$
$
\colorbox{yellow}{$F_{\mathrm{avg}}=\frac{\Delta p}{\Delta t}=\frac{2 m v}{0.010 \mathrm{~s}} \approx 5.76 \mathrm{~N}$}
$
Q.2[(a) (i)].2021-May-Physics_paper_2__TZ1_SL
Topic: Circular motion
Given: A planet is in a circular orbit around a star. The speed of the planet is constant.
Discuss: why a centripetal force is needed for the planet to be in a circular orbit.
Answer/Explanation
Solution:
In a circular orbit, an object moves in a curved path, which means its velocity is constantly changing direction. This change in direction indicates the presence of an acceleration, which is called the centripetal acceleration.
According to Newton’s second law of motion, an object will accelerate if a net force acts on it. In the case of a planet in a circular orbit, the gravitational force between the planet and the star provides the net force that causes the centripetal acceleration.
Thus, a centripetal force is needed to provide the necessary net force to keep the planet moving in a circular path around the star. Without this centripetal force, the planet would move off in a straight line tangentially to its initial path, due to its inertia.