Question-1 :2022-may-Chemistry_paper_1__TZ2_HL
Topic:
Discuss: What is the concentration of chloride ions, in $\mathrm{mol} \mathrm{dm}^{-3}$, in a solution formed by mixing $200 \mathrm{~cm}^3$ of $1 \mathrm{~mol} \mathrm{dm}^{-3} \mathrm{HCl}$ with $200 \mathrm{~cm}^3$ of $5 \mathrm{~mol} \mathrm{dm}^{-3} \mathrm{NaCl}$ ?
A. $1$
B. $2$
C. $3$
D. $6$
Answer/Explanation
Solution:
To determine the concentration of chloride ions in the solution, we first need to calculate the total number of moles of chloride ions present in the solution. We can do this by using the formula:$$
\text { moles }=\text { concentration } \times \text { volume }
$$
For the hydrochloric acid solution:
$$\text{moles of chloride ions = concentration} \times \text{volume}$$
$$
\begin{aligned}
& =1 \mathrm{~mol} / \mathrm{dm}^3 \times(200 / 1000) d m^3 \\
& =0.2 \text { moles }
\end{aligned}
$$
For the sodium chloride solution:
$$\text{moles of chloride ions = concentration} \times \text{volume}$$
$$
\begin{aligned}
& =5 \mathrm{~mol} / \mathrm{dm}^3 \times(200 / 1000) \mathrm{dm}^3 \\
& =1 \mathrm{moles}
\end{aligned}
$$
The total number of moles of chloride ions in the solution is therefore:
$$
0.2 \text { moles }+1 \text { moles }=1.2 \text { moles }
$$
Finally, we can calculate the concentration of chloride ions in the solution by dividing the total number of moles by the total volume
$$\text{concentration}=\frac{ \text { moles }}{\text { Volume }}$$
$$
\begin{aligned}
& =\frac{1.2 ~\mathrm{moles}}{(200 / 1000+200 / 1000)\mathrm{dm}^3} \\
& =3 \mathrm{~mol} / \mathrm{dm}^3
\end{aligned}
$$
$\colorbox{yellow}{Correct Option : C }$
Question-2 :2022-may-Chemistry_paper_1__TZ2_HL
Topic:
Given: $30 \mathrm{~g}$ of an organic compound produces $44 \mathrm{~g} \mathrm{CO}_2$ and $18 \mathrm{~g} \mathrm{H}_2 \mathrm{O}$ as the only combustion products.
$$
M_{\mathrm{r}} \mathrm{CO}_2=44 \mathrm{M}_{\mathrm{r}} \mathrm{H}_2 \mathrm{O}=18
$$
Calculate: Which of the following is the empirical formula for this compound?
A. $\mathrm{CH}_2$
B. $\mathrm{CH}_3$
C. $\mathrm{CHO}$
D. $\mathrm{CH}_2 \mathrm{O}$
Answer/Explanation
Solution:
To determine the empirical formula of the organic compound, we need to find the ratio of the number of atoms of each element in the compound.
Let’s first find the number of moles of $\mathrm{CO}_2$ and $\mathrm{H}_2\mathrm{O}$ produced by the combustion of $30\mathrm{~g}$ of the compound.
The number of moles of $\mathrm{CO}_2$ is:
$$
\text { moles of } \mathrm{CO}_2=\frac{44 \mathrm{~g}}{44 \mathrm{~g} / \mathrm{mol}}=1 \mathrm{~mol}
$$
The number of moles of $\mathrm{H}_2\mathrm{O}$ is:
$$\text { moles of } \mathrm{H}_2 \mathrm{O}=\frac{18 \mathrm{~g}}{18 \mathrm{~g} / \mathrm{mol}}=1 \mathrm{~mol}$$
Next, we can find the number of moles of carbon and hydrogen in the compound using the balanced chemical equation for the combustion of the compound:
$$
\mathrm{C}_x \mathrm{H}_y+\frac{(x+2 y)}{4} \mathrm{O}_2 \rightarrow x \mathrm{CO}_2+\frac{y}{2} \mathrm{H}_2 \mathrm{O}
$$
From the equation, we can see that $1$ mole of the compound produces $x$ moles of $\mathrm{CO}_2$ and $y/2$ moles of $\mathrm{H}_2\mathrm{O}$. Therefore:
$$\begin{aligned} & x=\frac{1 \mathrm{~mol} \mathrm{CO}_2}{1 \mathrm{~mol} \text { of compound }}=1 \mathrm{~mol} \\ & y / 2=\frac{1 \mathrm{~mol} \mathrm{H}_2 \mathrm{O}}{1 \mathrm{~mol} \text { of compound }}=1 \mathrm{~mol}\end{aligned}$$
So, the empirical formula of the compound is $\mathrm{CH}_2\mathrm{O}$, which corresponds to a molecular mass of $30\mathrm{~g/mol}$.
$\colorbox{yellow}{$\mathrm{CH}_2\mathrm{O}$ (D)}$.
Question-3 :2022-may-Chemistry_paper_1__TZ2_HL
Topic:
Discuss: Which graph represents the relationship between the amount of gas, $\mathrm{n}$, and the absolute temperature, $\mathrm{T}$, with all other variables in the ideal gas equation, $P V=n R T$, held constant?
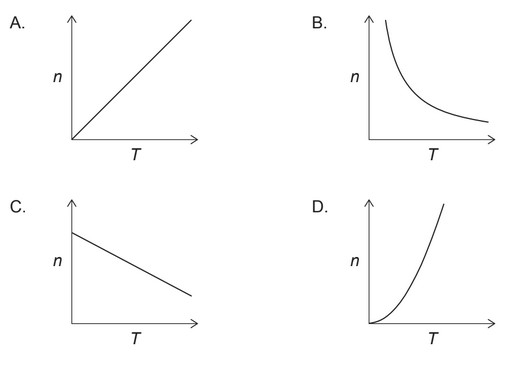
Answer/Explanation
Solution:
The ideal gas equation is given by $PV = nRT$, where $P$ is the pressure, $V$ is the volume, $n$ is the amount of gas in moles, $R$ is the gas constant, and $T$ is the absolute temperature.
If we hold the pressure, volume, and amount of gas constant, then the ideal gas equation becomes $T = \frac{PV}{nR}$. This means that the temperature is directly proportional to the product of pressure and volume, and inversely proportional to the amount of gas.
Therefore, if we plot $n$ on the x-axis and $T$ on the y-axis, with constant pressure and volume, we should see an inverse relationship between $n$ and $T$. This is because as the amount of gas decreases, the temperature must also decrease to maintain a constant pressure and volume.
So, the correct graph would be one where we see an inverse relationship between $n$ and $T$. Here is graph:
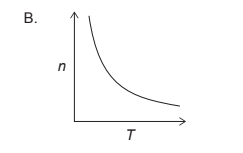
Question-4 :2022-may-Chemistry_paper_1__TZ2_HL
Topic:
Discuss: What is the relative atomic mass of an element with the following mass spectrum?
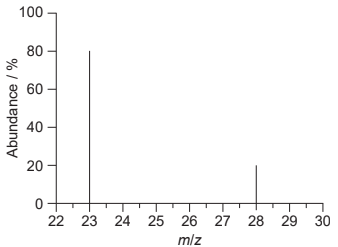
A. $23$
B. $24$
C. $25$
D. $28$
Answer/Explanation
Solution:
$
\begin{aligned}
& \text{The relative atomic mass}=\\
&\frac{\left[\text { atomic mass of }{ }^{23} \mathrm{X} \times \text { abundance of }{ }^{23} \mathrm{X}\right]+\left[\text { atomic mass of }{ }^{28} \mathrm{X} \times \text { abundance of }{ }^{28} \mathrm{X}\right]}{\text { abundance of }{ }^{23} \mathrm{X}+\text { abundance of }{ }^{28} \mathrm{X}} \\
& \Rightarrow \frac{[23 \times 80]+[28 \times 20]}{80+20}=24~ \mathrm{amu}
\end{aligned}
$
$\colorbox{yellow}{Correct Option : B }$
Question-5 :2022-may-Chemistry_paper_1__TZ2_HL
Topic:
Discuss: What is the correct order for increasing first ionization energy?
A. $\mathrm{Na}<\mathrm{Mg}<\mathrm{Al}$
B. $\mathrm{Na}<\mathrm{Al}<\mathrm{Mg}$
C. $\mathrm{Al}<\mathrm{Mg}<\mathrm{Na}$
D. $\mathrm{Al}<\mathrm{Na}<\mathrm{Mg}$
Answer/Explanation
Solution:
The first ionization energy is the energy required to remove one electron from a neutral atom in the gaseous state. As we move from left to right across a period in the periodic table, the first ionization energy generally increases due to the increasing effective nuclear charge, which attracts the electrons more strongly.
Sodium (Na), magnesium (Mg), and aluminum (Al) are all located in the third period of the periodic table. Therefore, we need to consider their positions in relation to each other to determine their relative first ionization energies.
Sodium is located to the left of magnesium and aluminum in the periodic table, so it has the lowest effective nuclear charge and the lowest first ionization energy of the three. Therefore, option (A) cannot be correct.
Between magnesium and aluminum, aluminum has one more proton in its nucleus, resulting in a stronger effective nuclear charge and a higher first ionization energy. Therefore, option (D) cannot be correct.
Option (C) states that aluminum has a lower first ionization energy than magnesium and sodium, which is incorrect based on our reasoning above.
Therefore, the correct answer is option (B), which states that the correct order for $\colorbox{yellow}{increasing first ionization energy is $\mathrm{Na} < \mathrm{Al} < \mathrm{Mg}$}$. This is because sodium has the lowest first ionization energy, followed by aluminum, and then magnesium has the highest first ionization energy among the three.