Section A
Answer all questions. Answers must be written within the answer boxes provided. Working may be continued below the lines, if necessary.
1. [Maximum mark: 5]
The following table shows values of $f(x)$ and $g(x)$ for different values of $x$.
Both $f$ and $g$ are one-to-one functions.
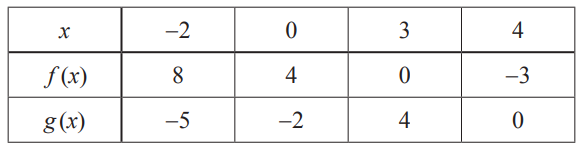
(a) Find $g(0)$.
(b) Find $(f \circ g)(0)$.
(c) Find the value of $x$ such that $f(x)=0$.
Answer/Explanation
1. (a) $g(0)=-2$
(b) evidence of using composite function
$
\begin{aligned}
& f(g(0)) \text { OR } f(-2) \\
& (f \circ g)(0)=8
\end{aligned}
$
(c) $x=3$
2. [Maximum mark: 5]
The $n^{\text {th }}$ term of an arithmetic sequence is given by $u_n=15-3 n$.
(a) State the value of the first term, $u_1$.
(b) Given that the $n^{\text {th }}$ term of this sequence is -33 , find the value of $n$.
(c) Find the common difference, $d$.
Answer/Explanation
(a) $u_1=12$
(b) $15-3 n=-33$
$
n=16
$
(c) valid approach to find $d$
$u_2-u_1=9-12$ OR recognize gradient is -3 OR attempts to solve $-33=12+15 d$
$
d=-3
$
3. [Maximum mark: 6]
Consider any three consecutive integers, $n-1, n$ and $n+1$.
(a) Prove that the sum of these three integers is always divisible by 3 .
(b) Prove that the sum of the squares of these three integers is never divisible by 3.
Answer/Explanation
(a) $(n-1)+n+(n+1)$ $=3 n$
which is always divisible by 3
(b) $(n-1)^2+n^2+(n+1)^2 \quad\left(=n^2-2 n+1+n^2+n^2+2 n+1\right)$ attempts to expand either $(n-1)^2$ or $(n+1)^2 \quad$ (do not accept $n^2-1$ or $n^2+1$ ) $=3 n^2+2$ demonstrating recognition that 2 is not divisible by 3 or $\frac{2}{3}$ seen after correct expression divided by 3 $3 n^2$ is divisible by 3 and so $3 n^2+2$ is never divisible by 3 OR the first term is divisible by 3 , the second is not OR $3\left(n^2+\frac{2}{3}\right) \quad$ OR $\quad \frac{3 n^2+2}{3}=n^2+\frac{2}{3}$ hence the sum of the squares is never divisible by 3
4. [Maximum mark: 6]
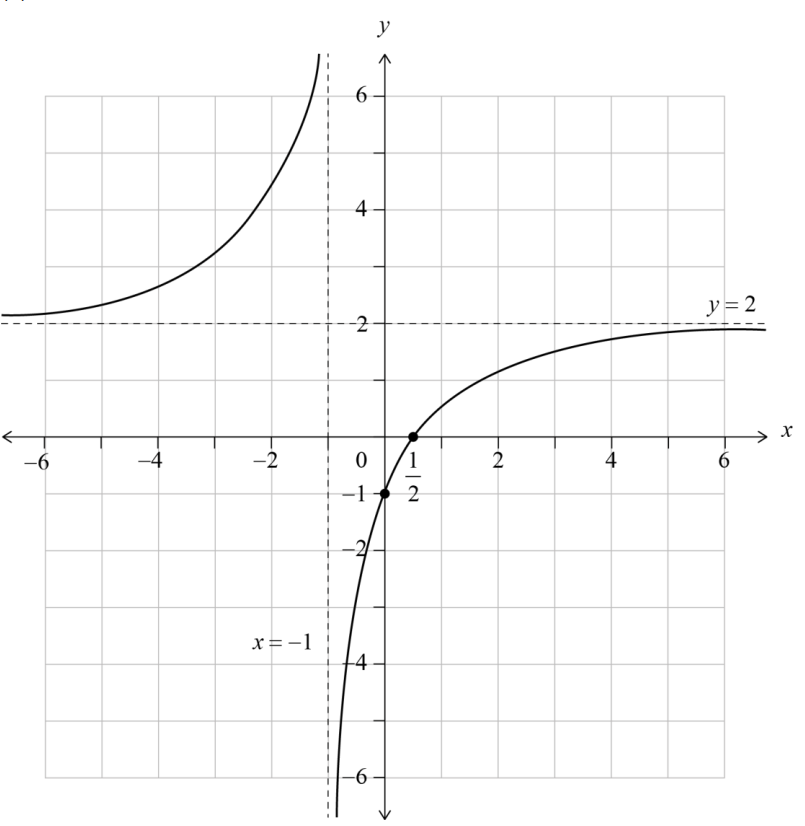
A function $f$ is defined by $f(x)=\frac{2 x-1}{x+1}$, where $x \in \mathbb{R}, x \neq-1$.
(a) The graph of $y=f(x)$ has a vertical asymptote and a horizontal asymptote.
Write down the equation of
(i) the vertical asymptote;
(ii) the horizontal asymptote.
(b) On the set of axes below, sketch the graph of $y=f(x)$.
On your sketch, clearly indicate the asymptotes and the position of any points of intersection with the axes.

(c) Hence, solve the inequality $0<\frac{2 x-1}{x+1}<2$.
Answer/Explanation
(a) (i) $x=-1$
(ii) $y=2$
(b)
rational function shape with two branches in opposite quadrants, with two correctly positioned asymptotes and asymptotic behaviour shown
Note: The equations of the asymptotes are not required on the graph provided there is a clear indication of asymptotic behaviour at $x=-1$ and $y=2$ (or at their FT asymptotes from part (a)).
axes intercepts clearly shown at $x=\frac{1}{2}$ and $y=-1$
(c) $x>\frac{1}{2}$
Note: Accept correct alternative correct notation, such as $\left(\frac{1}{2}, \infty\right)$ and $] \frac{1}{2}, \infty[$.
[Maximum mark: 5]
Find the least positive value of $x$ for which $\cos \left(\frac{x}{2}+\frac{\pi}{3}\right)=\frac{1}{\sqrt{2}}$.
Answer/Explanation
determines $\frac{\pi}{4}$ (or $45^{\circ}$ ) as the first quadrant (reference) angle attempts to solve $\frac{x}{2}+\frac{\pi}{3}=\frac{\pi}{4}$
Note: Award $\boldsymbol{M 1}$ for attempting to solve $\frac{x}{2}+\frac{\pi}{3}=\frac{\pi}{4}, \frac{7 \pi}{4}(, \ldots)$
$\frac{x}{2}+\frac{\pi}{3}=\frac{\pi}{4} \Rightarrow x<0$ and so $\frac{\pi}{4}$ is rejected
$\begin{aligned} & \frac{x}{2}+\frac{\pi}{3}=2 \pi-\frac{\pi}{4}\left(=\frac{7 \pi}{4}\right) \\ & x=\frac{17 \pi}{6} \quad \text { (must be in radians) }\end{aligned}$
6. [Maximum mark: 7]
Consider the binomial expansion $(x+1)^7=x^7+a x^6+b x^5+35 x^4+\ldots+1$ where $x \neq 0$ and $a, b \in \mathbb{Z}^{+}$.
(a) Show that $b=21$.
The third term in the expansion is the mean of the second term and the fourth term in the expansion.
(b) Find the possible values of $x$.
Answer/Explanation
(a) EITHER
recognises the required term (or coefficient) in the expansion
$
b x^5={ }^7 C_2 x^5 1^2 \quad \text { OR } \quad b={ }^7 C_2 \quad \text { OR }{ }^7 C_5
$
$
b=\frac{7 !}{2 ! 5 !}\left(=\frac{7 !}{2 !(7-2) !}\right)
$
correct working
$
\frac{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times 5 \times 4 \times 3 \times 2 \times 1} \quad \text { OR } \frac{7 \times 6}{2 !} \quad \text { OR } \quad \frac{42}{2}
$
OR
lists terms from row 7 of Pascal’s triangle $1,7,21, \ldots$
THEN
$
b=21
$
(b) $\quad a=7$
correct equation
$
21 x^5=\frac{a x^6+35 x^4}{2} \text { OR } \quad 21 x^5=\frac{7 x^6+35 x^4}{2}
$
correct quadratic equation
$
7 x^2-42 x+35=0 \text { OR } x^2-6 x+5=0 \text { (or equivalent) }
$
valid attempt to solve their quadratic
$
\begin{aligned}
& (x-1)(x-5)=0 \quad \text { OR } \quad x=\frac{6 \pm \sqrt{(-6)^2-4(1)(5)}}{2(1)} \\
& x=1, x=5
\end{aligned}
$
Note: Award final $\boldsymbol{A O}$ for obtaining $x=0, x=1, x=5$.
Section B
7. [Maximum mark: 15]
The following diagram shows part of the graph of a quadratic function $f$.
The graph of $f$ has its vertex at $(3,4)$, and it passes through point $\mathrm{Q}$ as shown.
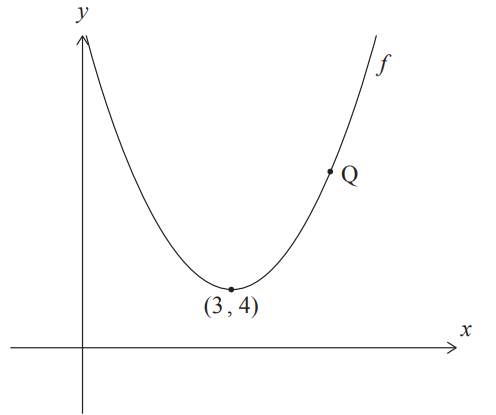
(a) Write down the equation of the axis of symmetry.
(b) The function can be written in the form $f(x)=a(x-h)^2+k$.
(i) Write down the values of $h$ and $k$.
(ii) Point $\mathrm{Q}$ has coordinates $(5,12)$. Find the value of $a$.
The line $L$ is tangent to the graph of $f$ at $\mathrm{Q}$.
(c) Find the equation of $L$.
Now consider another function $y=g(x)$. The derivative of $g$ is given by $g^{\prime}(x)=f(x)-d$, where $d \in \mathbb{R}$.
(d) Find the values of $d$ for which $g$ is an increasing function.
(e) Find the values of $x$ for which the graph of $g$ is concave-up.
Answer/Explanation
(a) $x=3$
Note: Must be an equation in the form ” $x=$ “. Do not accept 3 or $\frac{-b}{2 a}=3$.
(b) (i) $h=3, k=4 \quad\left(\right.$ accept $\left.a(x-3)^2+4\right)$
(ii) attempt to substitute coordinates of $\mathrm{Q}$
$
\begin{aligned}
& 12=a(5-3)^2+4,4 a+4=12 \\
& a=2
\end{aligned}
$
(c) recognize need to find derivative of $f$ $f^{\prime}(x)=4(x-3)$ or $f^{\prime}(x)=4 x-12$ $f^{\prime}(5)=8 \quad$ (may be seen as gradient in their equation) $y-12=8(x-5)$ or $y=8 x-28$
Note: Award $\boldsymbol{A} \boldsymbol{0}$ for $L=8 x-28$.
(d) METHOD 1
Recognizing that for $g$ to be increasing, $f(x)-d>0$, or $g^{\prime}>0$
The vertex must be above the $x$-axis, $4-d>0, d-4<0$
$
d<4
$
METHOD 2
attempting to find discriminant of $g^{\prime}$
$
(-12)^2-4(2)(22-d)
$
recognizing discriminant must be negative
$
\begin{aligned}
& -32+8 d<0 \text { OR } \Delta<0 \\
& d<4
\end{aligned}
$
(e) recognizing that for $g$ to be concave up, $g^{\prime \prime}>0$
$
g^{\prime \prime}>0 \text { when } f^{\prime}>0,4 x-12>0, x-3>0
$
$
x>3
$
[Maximum mark: 15]
Consider the functions $f(x)=\frac{1}{x-4}+1$, for $x \neq 4$, and $g(x)=x-3$ for $x \in \mathbb{R}$. The following diagram shows the graphs of $f$ and $g$.
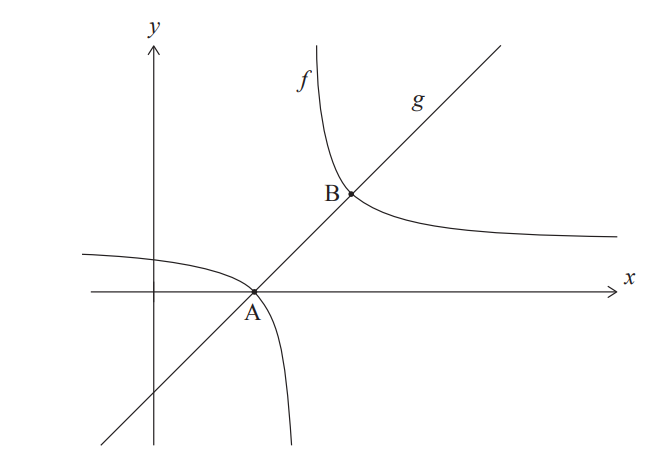
The graphs of $f$ and $g$ intersect at points A and B. The coordinates of A are $(3,0)$.
(a) Find the coordinates of B.
In the following diagram, the shaded region is enclosed by the graph of $f$, the graph of $g$, the $x$-axis, and the line $x=k$, where $k \in \mathbb{Z}$.

The area of the shaded region can be written as $\ln (p)+8$, where $p \in \mathbb{Z}$.
(b) Find the value of $k$ and the value of $p$.
Answer/Explanation
(a) $\frac{1}{x-4}+1=x-3$ $x^2-8 x+15=0$ OR $(x-4)^2=1$ valid attempt to solve their quadratic
$
\begin{aligned}
& (x-3)(x-5)=0 \text { OR } x=\frac{8 \pm \sqrt{8^2-4(1)(15)}}{2(1)} \text { OR }(x-4)= \pm 1 \\
& x=5(x=3, x=5) \text { (may be seen in answer) } \\
& \mathrm{B}(5,2) \text { (accept } x=5, y=2 \text { ) }
\end{aligned}
$
(b) recognizing two correct regions from $x=3$ to $x=5$ and from $x=5$ to $x=k$
$
\text { triangle }+\int_5^k f(x) \mathrm{d} x \text { OR } \int_3^5 g(x) \mathrm{d} x+\int_5^k f(x) \mathrm{d} x \text { OR } \int_3^5(x-3) \mathrm{d} x+\int_5^k\left(\frac{1}{x-4}+1\right) \mathrm{d} x
$
area of triangle is 2 OR $\frac{2 \cdot 2}{2}$ OR $\left(\frac{5^2}{2}-3(5)\right)-\left(\frac{3^2}{2}-3(3)\right)$ correct integration
correct integration
$
\int\left(\frac{1}{x-4}+1\right) \mathrm{d} x=\ln (x-4)+x(+C)
$
Note: Award $\boldsymbol{A} 1$ for $\ln (x-4)$ and $\boldsymbol{A} 1$ for $x$
Note: The first three $\boldsymbol{A}$ marks may be awarded independently of the $\boldsymbol{R}$ mark.
substitution of their limits (for $x$ ) into their integrated function (in terms of $x$ )
$
\begin{aligned}
& \ln (k-4)+k-(\ln 1+5) \\
& {[\ln (x-4)+x]_5^k=\ln (k-4)+k-5}
\end{aligned}
$
adding their two areas (in terms of $k$ ) and equating to $\ln p+8$
$
2+\ln (k-4)+k-5=\ln p+8
$
equating their non-log terms to 8 (equation must be in terms of $k$ )
$
\begin{aligned}
& k-3=8 \\
& k=11 \\
& 11-4=p \\
& p=7
\end{aligned}
$
[Maximum mark: 16]
A biased four-sided die with faces labelled 1,2,3 and 4 is rolled and the result recorded. Let $X$ be the result obtained when the die is rolled. The probability distribution for $X$ is given in the following table where $p$ and $q$ are constants.

For this probability distribution, it is known that $\mathrm{E}(X)=2$.
(a) Show that $p=0.4$ and $q=0.2$.
(b) Find $\mathrm{P}(X>2)$.
Nicky plays a game with this four-sided die. In this game she is allowed a maximum of five rolls. Her score is calculated by adding the results of each roll. Nicky wins the game if her score is at least ten.
After three rolls of the die, Nicky has a score of four.
(c) Assuming that rolls of the die are independent, find the probability that Nicky wins the game.
David has two pairs of unbiased four-sided dice, a yellow pair and a red pair.
Both yellow dice have faces labelled 1, 2, 3 and 4. Let $S$ represent the sum obtained by rolling the two yellow dice. The probability distribution for $S$ is shown below.

The first red die has faces labelled 1, 2,2 and 3 . The second red die has faces labelled $1, a, a$ and $b$, where $a<b$ and $a, b \in \mathbb{Z}^{+}$. The probability distribution for the sum obtained by rolling the red pair is the same as the distribution for the sum obtained by rolling the yellow pair.
(d) Determine the value of $b$.
(e) Find the value of $a$, providing evidence for your answer.
Answer/Explanation
(a) uses $\sum \mathrm{P}(X=x)=1$ to form a linear equation in $p$ and $q$ correct equation in terms of $p$ and $q$ from summing to 1 $p+0.3+q+0.1=1 \quad$ OR $\quad p+q=0.6 \quad$ (or equivalent) uses $\mathrm{E}(X)=2$ to form a linear equation in $p$ and $q$ correct equation in terms of $p$ and $q$ from $\mathrm{E}(X)=2$ $p+0.6+3 q+0.4=2$ OR $\quad p+3 q=1 \quad$ (or equivalent)
Note: The marks for using $\sum \mathrm{P}(X=x)=1$ and the marks for using $\mathrm{E}(X)=2$ may be awarded independently of each other.
evidence of correctly solving these equations simultaneously for example, $2 q=0.4 \Rightarrow q=0.2$ or $p+3 \times(0.6-p)=1 \Rightarrow p=0.4$ so $p=0.4$ and $q=0.2$
(b) valid approach
$
\begin{aligned}
& \mathrm{P}(X>2)=\mathrm{P}(X=3)+\mathrm{P}(X=4) \text { OR } \mathrm{P}(X>2)=1-\mathrm{P}(X=1)-\mathrm{P}(X=2) \\
& =0.3
\end{aligned}
$
(c) recognises at least one of the valid scores $(6,7$, or 8$)$ required to win the game
Note: Award $M 0$ if candidate also considers scores other than 6,7 , or 8 (such as 5).
let $T$ represent the score on the last two rolls a score of 6 is obtained by rolling $(2,4),(4,2)$ or $(3,3)$ $\mathrm{P}(T=6)=2(0.3)(0.1)+(0.2)^2(=0.1)$ a score of 7 is obtained by rolling $(3,4)$ or $(4,3)$ $\mathrm{P}(T=7)=2(0.2)(0.1)(=0.04)$ a score of 8 is obtained by rolling $(4,4)$
$
\mathrm{P}(T=8)=(0.1)^2(=0.01)
$
Note: The above 3 A1 marks are independent of each other.
$
\begin{aligned}
& P(\text { Nicky wins })=0.1+0.04+0.01 \\
& =0.15
\end{aligned}
$
(d) $3+b=8$
$
b=5
$
(e) METHOD 1
EITHER
$
\begin{aligned}
& \mathrm{P}(S=5)=\frac{4}{16} \\
& \mathrm{P}(S=a+2)=\frac{4}{16} \\
& \Rightarrow a+2=5
\end{aligned}
$
OR
$
\begin{aligned}
& \mathrm{P}(S=6)=\frac{3}{16} \\
& \mathrm{P}(S=a+3)=\frac{2}{16} \text { and } \mathrm{P}(S=5+1)=\frac{1}{16} \\
& \Rightarrow a+3=6
\end{aligned}
$
OR
$
\begin{aligned}
& \mathrm{P}(S=4)=\frac{3}{16} \\
& \mathrm{P}(S=a+1)=\frac{2}{16} \text { and } \mathrm{P}(S=1+3)=\frac{1}{16} \\
& \Rightarrow a+1=4
\end{aligned}
$
THEN
$
\Rightarrow a=3
$
METHOD 2
EITHER
correctly lists a relevant part of the sample space
for example, $\{S=4\}=\{(3,1),(1, a),(1, a)\}$ or $\{S=5\}=\{(2, a),(2, a),(2, a),(2, a)\}$ or $\{S=6\}=\{(3, a),(3, a),(1,5)\}$
$
a+3=6
$
OR
eliminates possibilities (exhaustion) for $a<5$
convincingly shows that $a \neq 2,4$
$a \neq 4$, for example, $\mathrm{P}(S=7)=\frac{2}{16}$ from $(2,5),(2,5)$ and so $(3, a),(3, a) \Rightarrow a+3 \neq 7$
THEN
$
\Rightarrow a=3
$