2022-May-Physics_paper_2__TZ2_SL – All Questions with detailed solution
Q.1(a).2022-May-Physics_paper_1__TZ2_SL
Topic: Forces
Given: Airboats are used for transport across a river. To move the boat forward, air is propelled from the back of the boat by a fan blade.
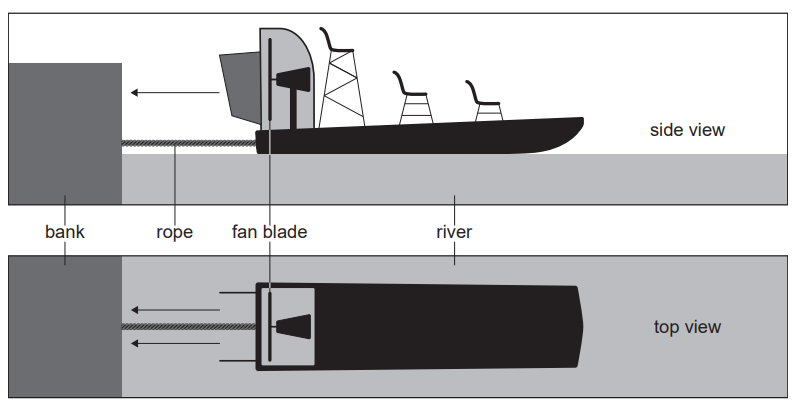
An airboat has a fan blade of radius $1.8 \mathrm{~m}$. This fan can propel air with a maximum speed relative to the boat of $20 \mathrm{~ms}^{-1}$. The density of air is $1.2 \mathrm{~kg} \mathrm{~m}^{-3}$.
Outline: why a force acts on the airboat due to the fan blade.
Answer/Explanation
Solution:
The fan blade of the airboat accelerates air to a certain speed relative to the boat. According to Newton’s third law, for every action, there is an equal and opposite reaction. Hence, when the fan accelerates air backward, the air exerts an equal and opposite force on the fan blade, propelling the boat forward. Therefore, a force acts on the airboat due to the fan blade.
Q.1[(b) (i)] .2022-May-Physics_paper_1__TZ2_SL
Topic: Forces
Given: In a test the airboat is tied to the river bank with a rope normal to the bank. The fan propels the air at its maximum speed. There is no wind.
Calculate: Show that a mass of about $240 \mathrm{~kg}$ of air moves through the fan every second.
Answer/Explanation
Solution:
We can calculate the mass of air moving through the fan every second using the formula:
$$\text{mass} = \text{density} \times \text{volume}$$
The volume of air moving through the fan per second is equal to the volume of air swept out by the fan blades per second. The volume of air swept out by the fan blades per second can be calculated using the formula for the volume of a cylinder:
$$\text{volume} = \pi r^2 v$$
where $r$ is the radius of the fan blade and $v$ is the speed of the air relative to the boat.
Substituting the given values, we get:
$$\text{volume} = \pi (1.8 \mathrm{~m})^2 (20 \mathrm{~ms}^{-1}) \approx 203 \mathrm{~m}^3 \mathrm{s}^{-1}$$
Substituting the given density of air, we get:
$$\colorbox{yellow}{$\text{mass} \approx (1.2 \mathrm{~kg} \mathrm{~m}^{-3}) \times (203 \mathrm{~m}^3 \mathrm{s}^{-1}) \approx 244 \mathrm{kgs}^{-1}$}$$
Therefore, the mass of air moving through the fan every second is about $240 \mathrm{~kg}$, as required.
Q.1[(b) (ii)].2022-May-Physics_paper_1__TZ2_SL
Topic: Forces
Calculate: Show that the tension in the rope is about $5 \mathrm{kN}$.
Answer/Explanation
Solution:
When the fan propels air at its maximum speed, it exerts a force on the air, and the air exerts an equal and opposite force on the fan blade. By Newton’s third law, the airboat experiences an equal and opposite force, which propels it forward.
However, in this case, the airboat is tied to the river bank with a rope normal to the bank. The tension in the rope balances the force on the boat due to the air. Therefore, we can find the tension in the rope by calculating the force on the boat due to the air.
The force on the boat due to the air can be calculated using the formula:
$$\text{force} = \text{mass} \times \text{acceleration}$$
where mass is the mass of air moving through the fan every second, and acceleration is the acceleration of the air relative to the boat.
From part (b)(i), we know that the mass of air moving through the fan every second is about $240 \mathrm{~kg}$. The acceleration of the air relative to the boat is the maximum speed of the air relative to the boat, which is $20 \mathrm{~ms}^{-1}$.
Therefore, the force on the boat due to the air is:
$$\colorbox{yellow}{$\text{force} = (244 \mathrm{~kg}) \times (20 \mathrm{~ms}^{-1}) \approx 4900 \mathrm{~N}$}$$
Since the rope is normal to the bank, the tension in the rope is equal to the force on the boat due to the air. Therefore, the tension in the rope is about $5 \mathrm{kN}$, as required.
Q.1[(c) (i)].2022-May-Physics_paper_1__TZ2_SL
Topic: Motion
Given: The rope is untied and the airboat moves away from the bank. The variation with time $t$ of the speed $v$ of the airboat is shown for the motion.
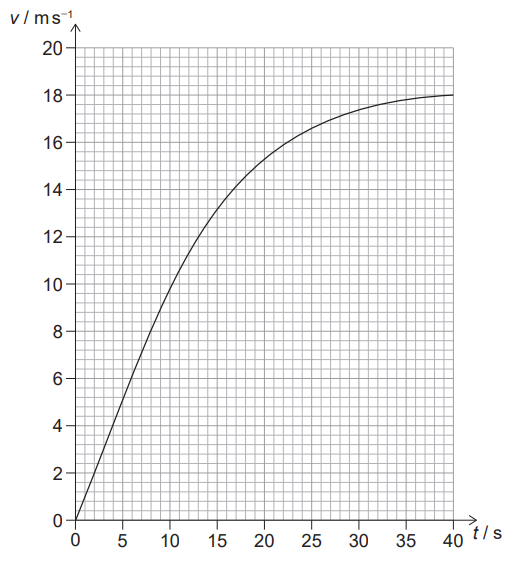
Estimate: the distance the airboat travels to reach its maximum speed.
Answer/Explanation
Solution:
Area under the graph is distance covered:
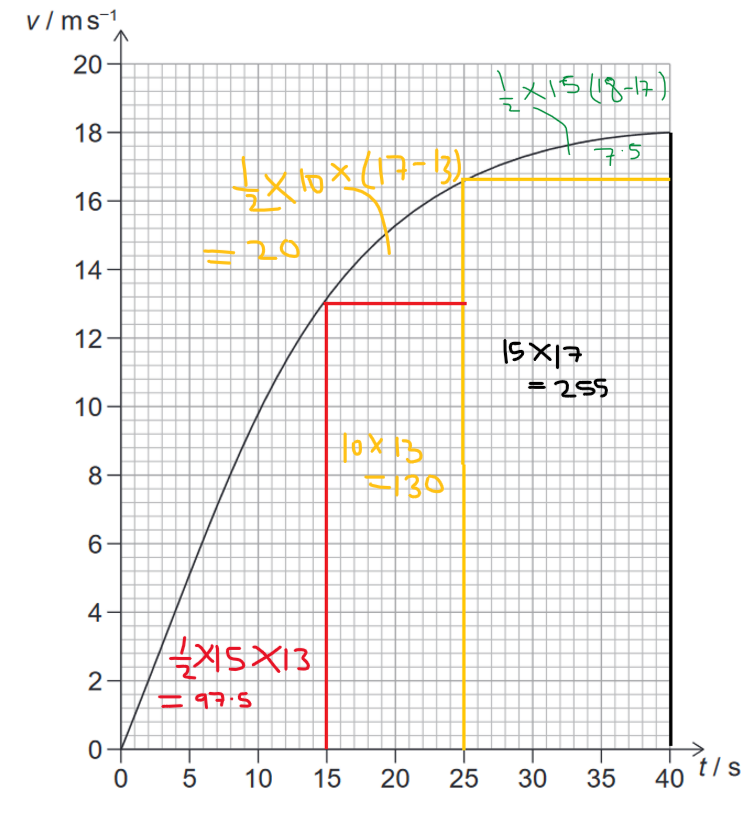
$\colorbox{yellow}{$\text{Area / distance covered}=97.5+130+20+255+7.5=510 \mathrm{~m}$}$
$\colorbox{orange}{Note: This is approximate area.}$
Q.1[(c) (ii)].2022-May-Physics_paper_1__TZ2_SL
Topic: Forces
Calculate: Deduce the mass of the airboat.
Answer/Explanation
Solution:
We have to find initial acceleration of boat. So we will calculate of acceleration as gradient at $t=0\ to\ t=1 \Rightarrow a= 1\mathrm{~m} \mathrm{~s}^{-2}$
using $F=ma$
$m=\frac{4900}{1}$
$\colorbox{yellow}{$m=\mathrm{4900~k g}$}$
Q.1(d).2022-May-Physics_paper_1__TZ2_SL
Topic: Circular motion
Given: The fan is rotating at 120 revolutions every minute.
Calculate: the centripetal acceleration of the tip of a fan blade.
Answer/Explanation
Solution:
The first step to solving this problem is to convert the given information into the appropriate units for the formula. We are given the radius of the fan blade, which is $r = 1.8 \mathrm{~m}$. We are also given the number of revolutions per minute, which is $n = 120 \mathrm{~rev/min}}$. We need to convert this to radians per second in order to use the centripetal acceleration formula.
One revolution is equal to $2\pi$ radians, so 120 revolutions per minute is equal to $120 \cdot 2\pi = 240\pi$ radians per minute. To convert this to radians per second, we divide by 60, so the angular velocity is $\omega = \frac{240\pi}{60} = 4\pi \mathrm{~rad/s}$.
Now we can use the formula for centripetal acceleration, which is $a_c = \frac{v^2}{r}$, where $v$ is the tangential velocity. Since the fan blade is rotating, the tangential velocity is equal to the product of the radius and the angular velocity, so $v = r\omega = 1.8 \mathrm{~m} \cdot 4\pi \mathrm{~rad/s} = 7.2\pi \mathrm{~m/s}$.
Plugging this into the formula for centripetal acceleration, we get:
$$\colorbox{yellow}{$a_c = \frac{v^2}{r} = \frac{(7.2\pi \mathrm{~m/s})^2}{1.8 \mathrm{~m}} \approx 285 \mathrm{~m/s^2}$}$$
Q.2(a).2022-May-Physics_paper_1__TZ2_SL
Topic: Modelling a gas
Given: A fixed mass of an ideal gas is contained in a cylinder closed with a frictionless piston. The volume of the gas is $2.5 \times 10^{-3} \mathrm{~m}^3$ when the temperature of the gas is $37^{\circ} \mathrm{C}$ and the pressure of the gas is $4.0 \times 10^5 \mathrm{~Pa}$.
Calculate: the number of gas particles in the cylinder.
Answer/Explanation
Solution:
We can use the ideal gas law to relate the number of moles of gas, the temperature, the pressure, and the volume of the gas:
$$PV = nRT$$
where $P$ is the pressure of the gas, $V$ is the volume of the gas, $n$ is the number of moles of gas, $R$ is the gas constant, and $T$ is the temperature of the gas in kelvin.
We are given the volume $V = 2.5 \times 10^{-3} \mathrm{~m}^3$, the temperature $T = 37^{\circ} \mathrm{C} = 310 \mathrm{~K}$ (converted to kelvin), and the pressure $P = 4.0 \times 10^5 \mathrm{~Pa}$. The gas constant $R$ is a known value: $R = 8.31 \mathrm{~J} \mathrm{mol}^{-1} \mathrm{K}^{-1}$.
Substituting these values, we get:
$$n = \frac{PV}{RT} = \frac{(4.0 \times 10^5 \mathrm{~Pa})(2.5 \times 10^{-3} \mathrm{~m}^3)}{(8.31 \mathrm{~J} \mathrm{mol}^{-1} \mathrm{K}^{-1})(310 \mathrm{~K})} \approx 0.388 \mathrm{~mol}$$
Therefore, there are about 0.033 moles of gas in the cylinder.
To calculate the number of gas particles, we can use Avogadro’s number $N_A = 6.022 \times 10^{23} \mathrm{~mol}^{-1}$:
$$\colorbox{yellow}{$\text{Number of particles} = nN_A = (0.388 \mathrm{~mol})(6.022 \times 10^{23} \mathrm{~mol}^{-1}) \approx 2.3 \times 10^{23} \mathrm{~particles}$}$$