2022-Nov-Physics_paper_2__TZ0_SL – All Questions with detailed solution
Q.1(a).2022-Nov-Physics_paper_2__TZ0_SL
Topic: Forces
Given: A raindrop falls vertically from rest.
Discuss: State the initial acceleration of the raindrop.
Answer/Explanation
Solution:
The initial acceleration of the raindrop is equal to the acceleration due to gravity, which is approximately 9.81 meters per second squared ($m/s^2$) directed downwards. This acceleration is caused by the gravitational force that the Earth exerts on the raindrop.
Q.1(b) .2022-Nov-Physics_paper_2__TZ0_SL
Topic: Motion
Given: The graph shows how the speed of the raindrop varies with time $t$.
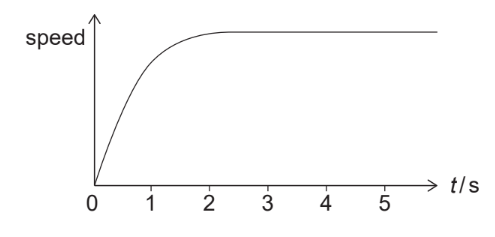
Explain: by reference to the vertical forces, how the raindrop reaches a constant speed.
Answer/Explanation
Solution:
The raindrop initially falls under the influence of gravity, so its speed increases as it falls due to the force of gravity acting on it. As the raindrop gains speed, the air resistance or drag force acting in the opposite direction to the motion increases. This opposing force due to air resistance becomes larger as the speed of the raindrop increases, until it eventually becomes equal in magnitude to the gravitational force acting on the raindrop.
At this point, the net force acting on the raindrop is zero, and the raindrop stops accelerating. Since the net force is zero, the raindrop continues to move at a constant speed known as the terminal velocity. The terminal velocity is the maximum speed that the raindrop can attain as it falls through the air. The forces acting on the raindrop are balanced, and there is no further acceleration, resulting in the raindrop moving at a constant speed.
Q.1[(c) (i)].2022-Nov-Physics_paper_2__TZ0_SL
Topic: Work, energy and power
Given: During the first $3.0 \mathrm{~s}$ of motion, the raindrop falls a distance of $21 \mathrm{~m}$ and reaches a speed of $9.0 \mathrm{~m} \mathrm{~s}^{-1}$. The mass of the raindrop is $34 \mathrm{mg}$. The temperature of the raindrop does not change.
Calculate: The energy transferred to the air during the first $3.0 \mathrm{~s}$ of motion. State your answer to an appropriate number of significant figures.
Answer/Explanation
Solution:
To determine the energy transferred to the air during the first $3.0 \mathrm{~s}$ of motion, we need to calculate the gravitational potential energy and the kinetic energy of the raindrop at the beginning and end of this time interval and find the difference between them. We can assume that all the work done by the gravitational force on the raindrop is dissipated as heat due to air resistance.
The gravitational potential energy of the raindrop at a height $h$ above the ground is given by:
$$
E_{\mathrm{pot}}=m g h
$$
where $m$ is the mass of the raindrop, $g$ is the acceleration due to gravity, and $h$ is the height above the ground.
At the beginning of the $3.0 \mathrm{~s}$ interval, the raindrop is at rest and has zero kinetic energy. Its gravitational potential energy is:
$$
E_{\mathrm{pot}, \mathrm{i}}=m g h_{\mathrm{i}}=(34 \mathrm{mg})\left(9.81 \mathrm{~m} / \mathrm{s}^2\right)(21 \mathrm{~m})=7.0 \times 10^{-3} \mathrm{J}
$$
where $h_\mathrm{i}$ is the initial height of the raindrop.
At the end of the $3.0 \mathrm{~s}$ interval, the raindrop has reached a speed of $9.0 \mathrm{~m/s}$ and has a kinetic energy given by:
$$
E_{\text {kin, } \mathrm{f}}=\frac{1}{2} m v_{\mathrm{f}}^2=\frac{1}{2}(34 \mathrm{mg})(9.0 \mathrm{~m} / \mathrm{s})^2=1.4 \times 10^{-3} \mathrm{J}
$$
where $v_\mathrm{f}$ is the final speed of the raindrop.
The energy transferred to the air during the first $3.0 \mathrm{~s}$ of motion is:
$$
\colorbox{yellow}{$\Delta E=E_{\mathrm{pot}, \mathrm{i}}-E_{\mathrm{kin}, \mathrm{f}}=7.0 \times 10^{-3}-1.4 \times 10^{-3} \mathrm{J}=5.6 \times 10^{-3} \mathrm{J}$}
$$
Q.1[(c) (ii)].2022-Nov-Physics_paper_2__TZ0_SL
Topic: Work, energy and power
Describe: The energy change that takes place for $t>3.0 \mathrm{~s}$.
Answer/Explanation
Solution:
For $t > 3.0 \mathrm{~s}$, the raindrop continues to fall at a constant speed known as the terminal velocity. At this point, the opposing air resistance force acting on the raindrop is equal in magnitude to the gravitational force, resulting in zero net force and zero net work done on the raindrop.
Since there is no net work done on the raindrop, there is no change in the total mechanical energy (the sum of kinetic and potential energy) of the system. However, energy is still being transferred from the raindrop to the air due to air resistance. The work done by the gravitational force is converted into heat as the raindrop falls through the air, which is then transferred to the air as thermal energy due to the friction between the air molecules and the raindrop.
Therefore, for $t > 3.0 \mathrm{~s}$, the potential energy of the raindrop continues to be converted into kinetic energy, which remains constant at the terminal velocity. The energy lost by the raindrop due to air resistance is converted into thermal energy, which is transferred to the surrounding air.
Q.2[(a) (i)].2022-Nov-Physics_paper_2__TZ0_SL
Topic: Thermal concepts
Given: A solar heating panel is placed on the roof of a house in order to heat water in a storage tank. The rest of the roof is covered with tiles.
On a certain day, the intensity of the solar radiation that is incident perpendicular to the surface of the panel is $680 \mathrm{Wm}^{-2}$.
The following data are available.
Mass of the water in the tank $=250 \mathrm{~kg}$
Initial temperature of the water in the tank $=15^{\circ} \mathrm{C}$
Specific heat capacity of water $=4200 \mathrm{Jkg}^{-1} \mathrm{~K}^{-1}$
Overall efficiency of the heating system $=0.30$
Albedo of the roof tiles $=0.20$
Emissivity of the roof tiles $=0.97$
Calculate: The minimum area of the solar heating panel required to increase the temperature of all the water in the tank to $30^{\circ} \mathrm{C}$ during a time of 1.0 hour.
Answer/Explanation
Solution:
Using the equations for energy required and energy available, we can solve for the area of the solar heating panel needed:
$\text{energy required} = m \times c \times \Delta T = 250 \times 4200 \times (30-15) = 1575 \times 10^4 J$
$\text{energy available} =\text{efficiency \times \text{intensity} \times t \times A = 0.30 \times 680 \times 3600 \times A = 734400A$
Setting the two equations equal to each other and solving for A:
$3.15 \times 10^7 = 734400A$
$\colorbox{yellow}{$A = \frac{1575 \times 10^4}{734400} = 42.9 \approx 22 \mathrm{~m}^2$}$