2023-Nov-Physics_paper_1__TZ0_HL
Topic: Physical Quantity
Given:The resistive force \(F\) that acts on an object moving through a fluid at speed \(v\) is given by \(F=k v\) where \(k\) is a constant.
Calculate: unit of \(k\) ?
A. \(\mathrm{Ns}^{-1}\)
B. \(\mathrm{Nms}^{-1}\)
C. \(\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-3}\)
D. \(\mathrm{kg} \mathrm{s}^{-1}\)
▶️Answer/Explanation
Ans:D
The resistive force (F) is given by \(F = k \cdot v\), where (F) is the force in Newtons (N), (v) is the velocity in meters per second (m/s), and (k) is a constant.
The unit of (k) can be determined by rearranging the equation to solve for (k):
\(k = \frac{F}{v}\)
Given that the unit of force (F) is Newtons (N) and the unit of velocity (v) is meters per second (m/s), the unit of (k) is Newtons per meter per second \((\mathrm{N/(m/s)})\), which simplifies to \(\mathrm{kg/s}\).
2023-Nov-Physics_paper_1__TZ0_HL
Topic: Motion (Graph related Problems)
Given: The graph shows the variation of the acceleration a with time t of an object moving in a straight line.
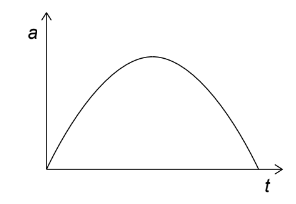
Discuss: Which graph shows the variation of the velocity v of the object with time t?
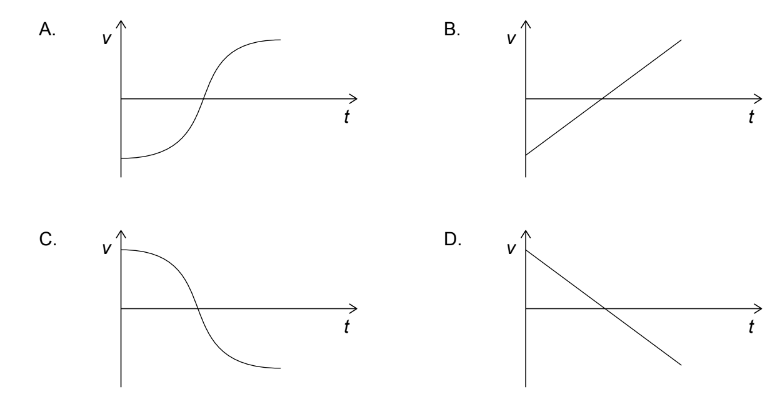
▶️Answer/Explanation
Ans:A
The graph given in the problem shows the acceleration ‘a’ of an object over time ‘t’. The graph is a downward parabola, which suggests that the acceleration is decreasing over time.
The velocity of an object is the integral of its acceleration. Since the acceleration is decreasing, the velocity should be represented by a graph that is decreasing at an increasing rate.
2023-Nov-Physics_paper_1__TZ0_HL
Topic: Projectile Motion
Given: A projectile moving in air has the path shown.
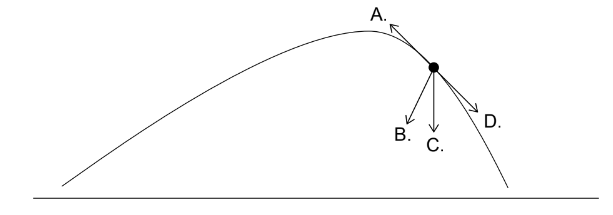
Discuss: direction of the net force at the point shown?
▶️Answer/Explanation
Ans:B
In the case of a projectile moving in air, the only significant force acting on it (ignoring air resistance) is gravity. Gravity acts downward towards the center of the Earth.
So, regardless of the point in the path of the projectile, the direction of the net force is always vertically downward. This is true even at the peak of the trajectory, where the velocity of the projectile is momentarily zero but the acceleration (and hence the net force) is still acting downward due to gravity.
If we take air resistance into account, the net force on the projectile will not be just vertically downward due to gravity. Air resistance acts in the direction opposite to the motion of the projectile.
At the point shown in the image, the projectile is moving upwards and to the right. Therefore, the air resistance will be acting downwards and to the left.
So, the net force will be a combination of the downward gravitational force and the air resistance. The exact direction will depend on the relative magnitudes of these two forces. If the air resistance is significant compared to the weight of the projectile, the net force could be angled more to the left.
2023-Nov-Physics_paper_1__TZ0_HL
Topic: Forces
Given:The diagram shows two blocks of mass \(m\) and \(M\) in contact on a frictionless surface. A force \(F\) is applied on the block of mass \(m\) and causes the blocks to move with an acceleration \(a\).
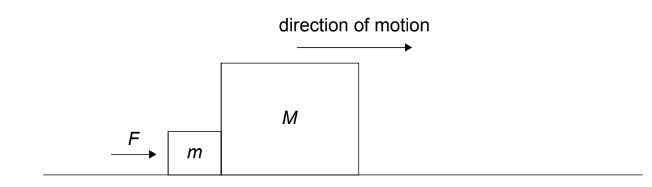
Calculate: the force that the block of mass \(M\) is exerting on the block of mass \(m\) ?
A. \(m a\)
B. \(M a\)
C. \((M+m) a\)
D. \(\frac{m}{M+m} a\)
▶️Answer/Explanation
Ans:B
As whole system is moving with same acceleration.
Free body diagram of system , only force action on M is normal between them .
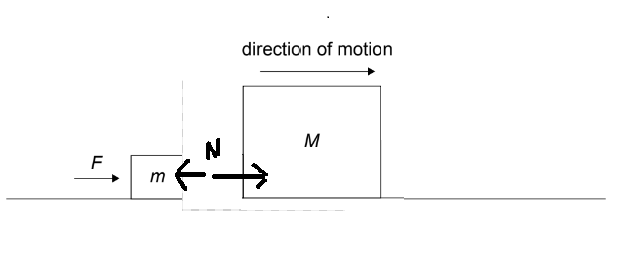
\(N= M \times a\)
2023-Nov-Physics_paper_1__TZ0_HL
Topic: Forces
Given:The diagram shows a block of mass \(m\) sliding at constant speed down an inclined plane. The plane makes an angle \(\theta\) with the horizontal.
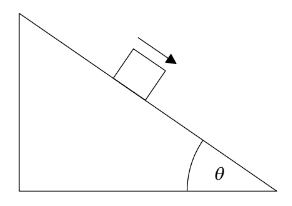
The coefficient of dynamic friction between the block and the plane is \(\mu_{\mathrm{D}}\) and the magnitude of the normal reaction force on the block is \(N\).
Calculate: \(\theta\) ?
A. \(\cos ^{-1}\left(\frac{m g}{\mu_{\mathrm{D}} N}\right)\)
B. \(\cos ^{-1}\left(\frac{\mu_D N}{m g}\right)\)
C. \(\sin ^{-1}\left(\frac{m g}{\mu_{\mathrm{D}} N}\right)\)
D. \(\sin ^{-1}\left(\frac{\mu_{\mathrm{D}} N}{m g}\right)\)
▶️Answer/Explanation
Ans:D
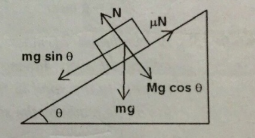
The forces acting on the block are:
- The gravitational force (mg), which can be decomposed into two components: one parallel to the plane \((mg \sin \theta)\) and one perpendicular to the plane \((mg \cos \theta))\.
- The normal force (N), which is equal to the component of the gravitational force perpendicular to the plane \(N = mg \cos \theta\).
- The frictional force, which is equal to the product of the coefficient of dynamic friction and the normal force \((\mu_D N)\). Since the block is sliding at a constant speed, the frictional force is equal to the component of the gravitational force parallel to the plane \((\mu_D N = mg \sin \theta)\).
From the equation \(\mu_D N = mg \sin \theta\), we can solve for \(\theta\):
\[\theta = \sin^{-1}\left(\frac{\mu_D N}{mg}\right)\]