First-Order Rate Law
- Order = 1 → changing the reactant concentration has an identical effect on the reaction rate (same factor)
- Rate Law =
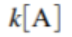
- If a plot of ln[A] versus time is a straight line → reaction is first order
- Integrated First Order rate law:
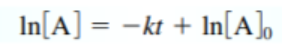(on reference sheet)- Subzero = initial molarity
- Sub t = molarity after some time has gone by
- Y = mx + b
- Rate constant = slope of line; y-int = initial value of molarity
Half-Life of a First-Order Reaction
- Half life: the time required for a reactant to reach half its original concentration (on RFS)
- The half-life of a 1st-order reaction is only dependent on K (NOT on concentration)
- A constant time is required to reduce the concentration of the reactant by half, and then by half again
- All type of radioactive decay is first-order
- A constant time is required to reduce the concentration of the reactant by half, and then by half again
Second-Order Reaction
- Order = 2 → changing reactant concentration will affect the reaction rate to the square of the change in the reactant
- Rate Law: Rate =
- Integrated Rate Law:
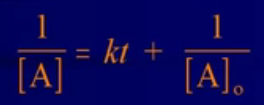(on ref. sheet) - If a plot of 1/[A] versus time is a straight line → reaction is second order
Half-Life of a Second Order Reaction
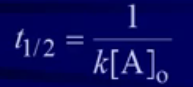(not on RFS)- The half-life of a second-order reaction depends on both K and the initial concentration [A]₀
- Finding half-life of 2nd order reaction → Pick any value for initial, plug in value for final answer that is half of initial value
- To find half-life must be given value of k
Zero-Order Rate Law
- Order = 0 → a change in reactant concentration has no effect on the rate
- Reactant will not appear in the overall rate law for the equation
- Rate Law: Rate = k
- Integrated rate law is
: - If a plot of [reactant] versus time is a straight line → reaction is zero-order