Introduction to Solubility Equilibria
- For solids dissolving to form aqueous solutions
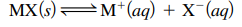
- Ksp = solubility product constant =
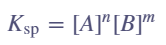
- Ksp value depends on ion concentration → more cations & anions = higher value
- Solids not included in equilibrium expression because the concentration does not change
- Only affected by temp
- Ksp = solubility product constant =
- Solubility = s = concentration of solid that dissolves
- Solubility has the same units as molarity (moles/liters)
- Solubility can vary with different factors → can speed or slow down the attainment of equilibrium but not its value
- Ex: Speed up by increasing surface area (grinding up the solid or stirring the solution); decrease as with common ion effect
Solubility Product Practice
- Type 1: Given solubility → calculate Ksp value
- Write out balanced equation & ICE table
- S instead of x → solubility is our s that will plug in
- Type 2: Given Ksp → calculate solubility:
- Write out balanced equation and ICE table
- Solve for s
Relative Solubilities
- In questions, will be given salts and must be able to decide which one is more soluble
- Ksp will only allow us to compare the solubility of salts that fall apart into the same number of ions
- Bigger Ksp value = more soluble
- Ex:
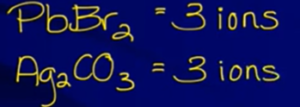same number of ions so can compare - Ex:
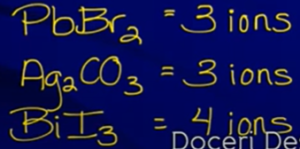diff number ions so can’t use Ksp to compare- Will have to solve for solubility (s) and compare those → bigger s value = more soluble
Calculations Involving Precipitation/Will a Precipitate Form?
- Must calculate Q and compare it to Ksp
- Focus on the compound whose Ksp value has been given and write balanced equation for how it breaks up
- Steps:
- Set up Q using FINAl Molarity (if not given use M1V1 = M2V2)
- Do M1V1 = M2V2 for both solutions → plug in the 2 M2 into Q
- Note: V2 = volume of the two solutions combined
- Do M1V1 = M2V2 for both solutions → plug in the 2 M2 into Q
- Set up Q using FINAl Molarity (if not given use M1V1 = M2V2)
- Q > Ksp → Precipitation
- Q < Ksp → No precipitate
- Q = Ksp → Equilibrium
