Gibbs Free Energy and Thermodynamic Favorability
- Gibbs Free Energy: available energy of substance that can be used for work
- Used to predict if a chemical reaction will occur spontaneously
- -ΔG° = the forward reaction is thermodynamically favored
- The reaction favors the products
- +ΔG° = not thermodynamically favored → not going to occur on its own
- The reaction favors the reactants
- Note: when see f in a question, use this equation
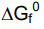of an element in its standard state is zero- Units: kJ
- Method #1 for calculating Free Energy Change (for reactions at constant temp)
- ΔG° = 0 → are at equilibrium
- Often when substance is at phase change → if at MP/BP or phase change are at equilibrium
- Find MP/BP = set ΔG° equal to 0 and solve for T
- Units must be the same!
- ΔG° = 0 → are at equilibrium
- Method #2: use Hess law
Effect of ΔH and ΔS on Spontaneity
Direction of Heat Flow
- Exothermic reactions usually increase the entropy of surroundings → are favored (bcuz heat is not required for the process)
- Endothermic reactions usually decrease the entropy of surroundings → are not favored (bcuz heat is required)
ΔS | ΔH | Favorability and Value of ΔG |
+ | – | Favored at all temp (ΔG always negative) |
+ | + | Favored at high temp (ΔG negative) ΔG positive at low temp |
– | – | Favored at low temp (ΔG negative) |
– | + | Not favored at any temp (ΔG always positive) → never spontaneous |
- +ΔH = not favorable; -ΔH = favorable
- Reactions can be ‘driven by enthalpy’ (where a very exothermic reaction (- ΔH)) overcomes a decrease in entropy) or ‘driven by entropy’ where an endothermic reaction occurs because of a highly positive ΔS
- Note: Hess’s law works the same for ΔG° & ΔS° as it does for ΔH°