Topics covered in this chapter:

Energy
Notes: energy: the ability to cause macroscopic objects or microscopic particles to increase their velocity; or their ability to increase their velocity due to the effects of a force field.
In plain English, if we apply mechanical energy to a physical object, the object will either move faster (think of pushing a cart), heat up, or have the ability to suddenly move when we let go of it (think of stretching a rubber band).
Energy is a scalar quantity, meaning that it does not have a direction. Energy can be transferred from one object (or collection of objects) to another.
Energy is a “conserved” quantity in physics, which means it cannot be created or destroyed, only changed in form.”
” More properly, the combination of mass and energy is conserved. Einstein’s equation states that mass can be converted to energy via the relationship $E=m c^2$.
Energy is measured in joules $(\mathrm{J})$ :
$
1 \mathrm{~J} \equiv 1 \mathrm{~N} \cdot \mathrm{m} \equiv 1 \frac{\mathrm{kg} \cdot \mathrm{m}^2}{\mathrm{~s}^2}
$
Potential Energy
Potential energy is the energy that an object has because the object is in a force field. When the object is released, the force field will act on the object to cause it to gain kinetic energy.
Systems and Potential Energy
Recall that a system is a collection of objects for the purpose of describing the interaction of objects within vs. outside of that collection. The surroundings is all of the objects outside of the system (“everything else”).
Potential energy is a property of the energy relationship between two objects within a system, because of a field that can change the relationship between two or more objects within the system. A single, isolated object cannot have potential energy.
Recall the following definition of a force field:
force field: a region in which an object experiences a force because of some property of that object.
•gravitational field (or “gravity field”): a force field in which an object experiences a force because of and proportional to its mass.
• electric field: a force field in which an object experiences a force because of and proportional to its electric charge.

For example, in the coyote-anvil system pictured to the right, both Wile E. Coyote and the anvil have negligible potential energy. (There is a tiny amount of gravitational attraction between them-assuming the anvil has a mass of $200 \mathrm{~kg}$ and the coyote has a mass of $20 \mathrm{~kg}$, the gravitational attraction between them would be $3 \times 10^{-7} \mathrm{~N}$.) However, the Earth can attract the entire coyote-anvil system toward itself.
On the other hand, in the coyote-anvil-Earth system, the anvil and the coyote each have potential energy with respect to the Earth. As the coyote and anvil both fall toward the Earth, that potential energy changes to kinetic energy, causing both the coyote and the anvil to fall faster and faster…
Refer to Systems on page 246 and Gravitational Fields on page 254 for a brief review.
Gravitational Potential Energy
As discussed earlier, a gravity field is a region (near a massive object like the Earth) in which the force of gravity acts on all objects that have mass. Gravitational potential energy is the work that the gravity field has the potential to do on the object because of its mass.
The gravitational potential energy of an object is determined by the gravitational field (equal to the acceleration due to gravity, $\overrightarrow{\boldsymbol{g}}$, which is approximately $10 \frac{\mathrm{m}}{\mathrm{s}^2}$ near the surface of the Earth), the mass of the object, and the object’s distance above the ground (height, which is the distance over which the force of gravity is able to do work on the object).
$
U_g=F_g h=m g h
$
Remember that gravitational potential energy exists only when there are two or more objects in a system, and at least one of the objects has a significant gravitational field.
Kinetic Energy
The kinetic energy of an object is related to its mass and velocity. An object has translational kinetic energy (the kinetic energy of an object or system that is moving in the $x y$ plane or $x y z$ space) if its center of mass is moving. Translational kinetic energy is given by the equation:
$
K=\frac{1}{2} m v^2
$
Note that a single object can have kinetic energy. An entire system can also have kinetic energy if the center of mass of the system is moving (has nonzero mass and velocity)
Kinetic energy exists both in linear systems and rotating systems. The above equation is for translational kinetic energy; rotational kinetic energy will be discussed in a separate topic.
Mechanical Energy
Mechanical energy is gravitational potential energy plus kinetic energy. Because potential energy and kinetic energy are easily interconverted, it is convenient to have a term that represents the combination of the two.
” In these notes, $K$ without a subscript is assumed to be translational kinetic energy. In problems with both translational and rotational kinetic energy, translational kinetic energy will be denoted as $K_t$ and rotational kinetic energy as $K_r$.
Thermal Energy
Kinetic energy is both a macroscopic property of a large object (i.e., something that is at least large enough to see), and a microscopic property of the individual particles (atoms or molecules) that make up an object. Thermal energy is the macroscopic energy that an object has due to the combined kinetic energies of its individual particles. (Heat is thermal energy added to or removed from a system.)
As we will see when we study thermal physics, temperature is the average microscopic kinetic energy of the individual particles that an object is made of. (Macroscopic) kinetic energy can be converted into thermal energy if the kinetic energy of a macroscopic object is turned into the individual kinetic energies of the molecules of that object and/or some other object. This can occur via friction or via a collision.
Chemical Potential Energy
In chemistry, chemical potential energy comes from the forces between particles (atoms or molecules), largely the electromagnetic forces attracting the atoms in a chemical bond. The energy absorbed or given off in a chemical reaction is the difference between the energies contained in the molecules before vs. after the reaction. If energy is given off by a reaction, it is absorbed by the particles, increasing their kinetic energy, which means the temperature increases. If energy is absorbed by a reaction, that energy must come from the kinetic energy of the particles, which means the temperature decreases.
Electrical Energy
Electrical energy is the energy that causes electrically charged particles to move through an electric circuit. The energy for this ultimately comes from some other source, such as chemical potential (i.e., a battery), mechanical energy (i.e., a generator), etc.
Work
Notes: work $(W)$ : mechanical energy (the application of a force over a distance) transferred into or out of a system. (J)
heat (Q): thermal energy transferred into or out of a system. (J) Heat is covered in more detail in the Introduction: Thermal Physics (Heat) unit that starts on page 605 , and in much more detail in Physics 2.
work $(W)$ : a change in the mechanical energy of an object or system caused by the application of a force over a distance.
heat (Q): a change in the thermal energy of a system. (Thermal energy is the total energy contained within the particles of the system.)
If you lift a heavy object off the ground, you are giving the object gravitational potential energy (in the object-Earth system). The Earth’s gravitational field can now cause the object to fall, turning the potential energy into kinetic energy. Therefore, we would say that you are doing work against the force of gravity.
Work is therefore the amount of energy that was added to the object $(\mathrm{W}=\Delta E)^*$. (In this case, because the work was turned into potential energy, we would say that $\mathrm{W}=\Delta U$.
Mathematically, work is also the dot product of the force vector and the displacement vector. Therefore, we can say that:
$
\Delta E=W=\overrightarrow{\boldsymbol{F}} \bullet \overrightarrow{\boldsymbol{d}}
$
Recall that the dot product is one of three ways of multiplying vectors. The dot product is a scalar (a number without a direction), and is equal to the product of the magnitudes of the force and distance, and the cosine of the angle between them. This means:
$
W=F d \cos \theta=F_{11} d
$
Where $F$ is the magnitude of the force vector $\overrightarrow{\boldsymbol{F}}, d$ is the magnitude of the displacement vector $\overrightarrow{\boldsymbol{d}}$, and $\theta$ is the angle between the two vectors. Sometimes $F \cos \theta$ is written as $F_{11}$, which means “the component of the force that is parallel to the direction of motion.”
Note that when the force and the displacement are in the same direction, the angle $\theta=0^{\circ}$ which means $\cos \theta=\cos \left(0^{\circ}\right)=1$. In this case, $F_{1 \mid}=F \cos \theta=(F)(1)=F$ and the equation reduces to $W=F d$.
Work is measured in newton-meters $(N \cdot m)$ or joules $(\mathrm{J})$.
$
1 \mathrm{~N} \cdot \mathrm{m} \equiv 1 \mathrm{~J} \equiv 1 \frac{\mathrm{kg} \cdot \mathrm{m}^2}{\mathrm{~s}^2}
$
Positive vs. Negative Work
Unlike most scalar quantities, work can be positive or negative.
•If the energy of an object or system increases because of work, then the work is positive, and we say that the work was done on the object or system.
•- If the energy of an object decreases, then the work is negative. We could say either that the work done on the object is negative, or we could say that (positive) work was done by the object instead.
* Many texts start with work as the application of force over a distance, and then discuss energy. Those texts then derive the work-energy theorem, which states that the two quantities are equivalent. In these notes, we instead started with energy, and then defined work as the change in energy. This presentation makes the concept of work more intuitive, especially when studying other energy-related topics such as thermodynamics.
Example:
A truck pushes a $1000 \mathrm{~kg}$ car up a $50 \mathrm{~m}$ hill. The car gained $U_g=m g h=(1000)(10)(50)=500000 \mathrm{~J}$ of potential energy. We could say that:
• $100000 \mathrm{~J}$ of work was done on the car (by the truck).
•$100000 \mathrm{~J}$ of work was done by the truck (on the car).
•$-100000 \mathrm{~J}$ of work was done on the truck (by the car).
A simple way to tell if a force does positive or negative work on an object is to use the equation $W=F_{11} d$. If the force and the displacement are in the same direction, then the work done by the force is positive. If the force and displacement are in opposite directions, then the work done by the force is negative.
Example:
Suppose a force of $750 \mathrm{~N}$ is used to push a cart against $250 \mathrm{~N}$ of friction for a distance of $20 \mathrm{~m}$. The work done by the force is $W=F_{1 \mid} d=(750)(20)=15000 \mathrm{~J}$. The work done by friction is $W=F_{11} d=(-250)(20)=-5000 \mathrm{~J}$ (negative because friction is in the negative direction). The total (net) work done on the cart is $15000+(-5000)=10000 \mathrm{~J}$
We could also figure out the net work done on the cart directly by using the net force: $W_{\text {net }}=F_{\text {net }, \|} d=(750-250)(20)=(500)(20)=10000 \mathrm{~J}$
Notes:
• If the displacement is zero, no work is done by the force. E.g., if you hold a heavy box without moving it, you are exerting a force (counteracting the force of gravity) but you are not doing work.
•If the net force is zero, no work is done by the displacement (change in location) of the object. E.g., if a cart is sliding across a frictionless air track at a constant velocity, the net force on the cart is zero, which means no work is being done.
• If the displacement is perpendicular to the direction of the applied force $\left(\theta=90^{\circ}\right.$, which means $\cos \theta=0$ ), no work is done by the force. E.g., you can slide a very heavy object along a roller conveyor, because the force of gravity is acting vertically and the object’s displacement is horizontal, which means gravity and the normal force cancel, and you therefore do not have to do any work against gravity.
A roller conveyor:

Force vs. Distance Graphs
If the amount of force is changing as an object moves, work is the area under the graph of force vs. distance:
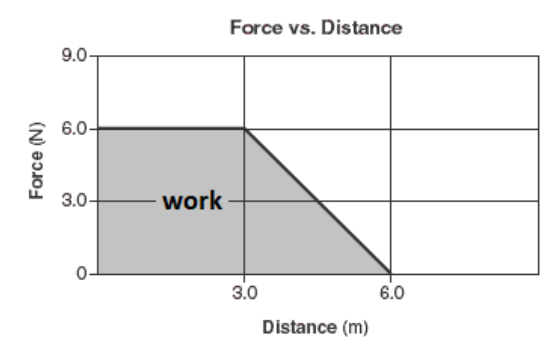
In the above example, a total of $27 \mathrm{~N} \cdot \mathrm{m}$ of work was done on the object: $18 \mathrm{~N} \cdot \mathrm{m}$ of work as the object moved from $0 \mathrm{~m}$ to $3 \mathrm{~m}$, and $9 \mathrm{~N} \cdot \mathrm{m}$ of work as the object moved from $3 m$ to $6 m$.
Once again, note the general rule that we have a formula for a quantity (work) that equals the quantity on the $y$-axis (force) times the change in the quantity on the $x$ axis (distance). Therefore, the value of the quantity (work) equals the area under the graph (force vs. distance)
Sample Problems:
Q: How much work does it take to lift a $60 . \mathrm{kg}$ box $1.5 \mathrm{~m}$ off the ground at a constant velocity over a period of $3.0 \mathrm{~s}$ ?
Answer/Explanation
A: The box is being lifted, which means the work is done against the force of gravity.
$
\begin{aligned}
& W=F_{11} \cdot d=F_g d \\
& W=F_g d=[m g] d=[(60)(10)](1.5)=[600](1.5)=900 \mathrm{~J}
\end{aligned}
$
Note that the amount of time it took to lift the box has nothing to do with the amount of work done.
It may be tempting to try to use the time to calculate velocity and acceleration in order to calculate the force. However, because the box is lifted at a constant velocity, the only force needed to lift the box is enough to overcome the weight of the box $\left(F_g\right)$.
In general, if work is done to move an object vertically, the work is done against gravity, and you need to use $a=g=10 \frac{\mathrm{m}}{s^2}$ for the acceleration when you calculate $F=m a$.
Similarly, if work is done to move an object horizontally, the work is not against gravity and either you need to know the force applied or you need to find it from the acceleration of the object using $F=m a$.
Conservation of Energy
Notes:
In a closed system (meaning a system in which there is no exchange of matter or energy between the system and the surroundings), the total energy is constant. Energy can be converted from one form to another. When this happens, the increase in any one form of energy is the result of a corresponding decrease in another form of energy.
In a system that has potential energy, kinetic energy and heat, the total energy is given by:
$
E_{\text {total }}=U+K+Q
$
In the following diagram, suppose that a student drops a ball with a mass of 2 kg from a height of 3 m.

Before the student lets go of the ball, it has $60 \mathrm{~J}$ of potential energy. As the ball falls to the ground, potential energy is gradually converted to kinetic energy. The potential energy continuously decreases and the kinetic energy continuously increases, but the total energy is always $60 \mathrm{~J}$. After the ball hits the ground, $60 \mathrm{~J}$ of work was done by gravity, and the $60 \mathrm{~J}$ of kinetic energy is converted to other forms. For example, if the ball bounces back up, some of the kinetic energy is converted back to potential energy. If the ball does not reach its original height, that means the rest of the energy was converted into other forms, such as thermal energy (the temperatures of the ball and the ground increase infinitesimally), sound, etc.
Work-Energy Theorem
We have already seen that work is the action of a force applied over a distance. A broader and more useful definition is that work is the change in the energy of an object or system. If we think of a system as having imaginary boundaries, then work is the flow of energy across those boundaries, either into or out of the system.
For a system that has only mechanical energy, work changes the amount of potential and/or kinetic energy in the system.
$
W=\Delta K+\Delta U
$
Although work is a scalar quantity, we use a positive number for work coming into the system (“work is done on the system”), and a negative number for work going out of the system (“the system does work on its surroundings”).
Note that the units for work and energy-newton-meters and joules-are equivalent.
$
1 \mathrm{~J} \equiv 1 \mathrm{~N} \cdot \mathrm{m} \equiv 1 \frac{\mathrm{kg} \cdot \mathrm{m}^2}{\mathrm{~s}^2}
$
Work-energy theorem problems will give you information related to the gravitational potential and/or kinetic energy of an object (such as its mass and a change in velocity) and ask you how much work was done.
A simple rule of thumb (meaning that it is not always strictly true) is:
• Potential energy is energy in the future (energy that is available for use).
• Kinetic energy is energy in the present (the energy of an object that is currently in motion).
• Work is the result of energy in the past (the result of potential or kinetic energy having acted on an object).
Conservation of Energy
In physics, if a quantity is “conserved”, that means when some change happens to a system, there is the same amount of that quantity after the change as there was before.
Energy Bar Charts
A useful way to represent conservation of energy is through bar graphs that represent kinetic energy (KE), gravitational potential energy (PE), and total mechanical energy (TME). (We use the term “chart” rather than “graph” because the scale is arbitrary and the chart is not meant to be used quantitatively.)
The following is an energy bar chart for a roller coaster, starting from point $A$ and traveling through points B, C, D, and E.

Notice, in this example, that:
1. The total mechanical energy always remains the same. (This the case in conservation of energy problems if there is no work added to or removed from the system.)
2. $\mathrm{KE}$ is zero at point $\mathbf{A}$ because the roller coaster is not moving. All of the energy is $\mathrm{PE}$, so $\mathrm{PE}=\mathrm{TME}$.
3. $P E$ is zero at point $D$ because the roller coaster is at its lowest point. All of the energy is $K E$, so $K E=T M E$.
4. At all points (including points $\mathbf{A}$ and $\mathbf{D}), \mathrm{KE}+\mathrm{PE}=\mathrm{TME}$
It can be helpful to sketch energy bar charts representing the different points in complicated conservation of energy problems. If energy is being added to or removed from the system, add an Energy Flow diagram to show energy that is being added to or removed from the system.
Solving Conservation of Energy Problems
Conservation of energy problems involve recognizing that energy is changing from one form to another. Once you have figured out what is being converted, calculate the amount energy that is converted, and use the equation for the new form to calculate the desired quantity.
In mechanics, conservation of energy problems usually involve work, gravitational potential energy, and kinetic energy:
$
\begin{aligned}
& W=F \bullet d=F d \cos \theta \text { (= Fd if force } \& \text { displacement are in the same direction) } \\
& U_g=m g h \\
& K=\frac{1}{2} m v^2
\end{aligned}
$
The general form of work-energy problems is:
$
\text { Total Energy Before }+ \text { Work }=\text { Total Energy After }
$
The strategy is to identify the types of energy before and after the change and write the above equation. Then replace each type of energy with its formula and solve.
Sample Problems:
Q: An $875 \mathrm{~kg}$ car accelerates from $22 \frac{\mathrm{m}}{\mathrm{s}}$ to $44 \frac{\mathrm{m}}{\mathrm{s}}$.
Answer/Explanation
A. Draw an energy bar chart representing the initial and final energies and the flow of energy into or out of the system.
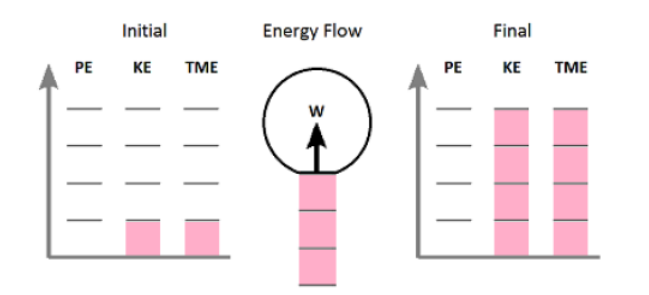
Notice that:
- The problem doesn’t mention a change in height, so we assume there isn’t one. This means the gravitational potential energy is zero, both before and after, and the only type of energy the car has in this problem is kinetic.
- The car is moving, both before and after, so it has kinetic energy. The car is moving faster at the end, so it has more kinetic energy at the end than at the beginning, and therefore more total mechanical energy at the end than at the beginning.
- Because the total energy at the end was more than at the beginning, work must have gone into the system.
b. What were the initial and final kinetic energies of the car? How much work did the engine do to accelerate it?
$
\begin{aligned}
\text { Before }+ \text { Work } & =\text { After } \\
T M E_{\text {before }}+W & =T M E_{a f t e r} \\
K_i+W & =K_f \\
\frac{1}{2} m v_i^2+W & =\frac{1}{2} m v_f^2 \\
\frac{1}{2}(875)(22)^2+W & =\frac{1}{2}(875)(44)^2 \\
211750+W & =847000 \\
W & =847000-211750=635250 \mathrm{~J}
\end{aligned}
$
Answers: $K_i=211750 \mathrm{~J} ; K_f=847000 \mathrm{~J} ; W=635250 \mathrm{~J}$
Rotational Work
Notes:
Just as work is done when a force causes an object to translate (move in a straight line), work is also done when a torque causes an object to rotate.
As with other equations for rotational motion, the rotational equation for work looks just like the linear (translational) equation, with each variable from the linear equation replaced by its analogue from the rotational equation.
In the equation for work, force is replaced by torque, and (translational) distance is replaced by rotational distance (angle):

Sample Problem
Q: How much work is done on a bolt when it is turned $30^{\circ}$ by applying a perpendicular force of $100 \mathrm{~N}$ to the end of a $36 \mathrm{~cm}$ long wrench?
Answer/Explanation
A: The equation for work is:
$
W=\tau \Delta \theta
$
The torque is:
$
\begin{aligned}
\tau & =r F_{\perp} \\
\tau & =(0.36)(100)=36 \mathrm{~N} \cdot \mathrm{m}
\end{aligned}
$
The angle, in radians, is:
$
\theta=30^{\circ} \times \frac{2 \pi \mathrm{rad}}{360^{\circ}}=\frac{\pi}{6} \mathrm{rad}
$
The angle, in radians, is:
$
\theta=30^{\circ} \times \frac{2 \pi \mathrm{rad}}{360^{\circ}}=\frac{\pi}{6} \mathrm{rad}
$
The work done on the bolt is therefore:
$
\begin{aligned}
& W=\tau \Delta \theta \\
& W=(36)\left(\frac{\pi}{6}\right) \\
& W=6 \pi=(6)(3.14)=18.8 \mathrm{~N} \cdot \mathrm{m}
\end{aligned}
$
Note that torque and work are different, unrelated quantities that both happen to have the same unit $(\mathrm{N} \cdot \mathrm{m})$. However, torque and work are not interchangeable! Notice that $36 \mathrm{~N} \cdot \mathrm{m}$ of torque produced $18.8 \mathrm{~N} \cdot \mathrm{m}$ of work because of the angle through which the torque was applied. If the angle had been different, the amount of work would have been different.
This is an example of why you cannot rely exclusively on dimensional analysis to set up and solve problems!
Rotational Kinetic Energy
Notes:
Just as an object that is moving in a straight line has kinetic energy, a rotating object also has kinetic energy.
The angular velocity (rate of rotation) and the translational velocity are related, because distance that the object must travel (the arclength) is the object’s circumference $(s=2 \pi r)$, and the object must make one complete revolution ( $\Delta \theta=2 \pi$ radians) in order to travel this distance. This means that for a rolling object:
$
\Delta \theta=2 \pi r
$
Just as energy can be converted from one form to another and transferred from one object to another, rotational kinetic energy can be converted into any other form of energy, including translational kinetic energy.
This is the principle behind log rolling. The two contestants get the log rolling quite fast. When one contestant fails to keep up with the log, some of the log’s rotational kinetic energy is converted to that contestant’s translational kinetic energy, which catapults them into the water:

In a rotating system, the formula for kinetic energy looks similar to the equation for kinetic energy in linear systems, with mass (translational inertia) replaced by moment of inertia (rotational inertia), and linear (translational) velocity replaced by angular velocity:
In the rotational equation, $l$ is the object’s moment of inertia (see Rotational Inertia starting on page 332 ), and $\omega$ is the object’s angular velocity.
Note: these problems make use of three relationships that you need to memorize:
$
s=r \Delta \theta \quad v_t=r \omega \quad a_t=r \alpha
$
Sample Problem:
Q: What is the rotational kinetic energy of a tenpin bowling ball that has a mass of $7.25 \mathrm{~kg}$ and a radius of $10.9 \mathrm{~cm}$ as it rolls down a bowling lane at $8.0 \mathrm{~m}$ ?
Answer/Explanation
A: The equation for rotational kinetic energy is:
$
K_r=\frac{1}{2} I \omega^2
$
We can find the angular velocity from the translational velocity:
$
\begin{aligned}
v & =r \omega \\
8.0 & =(0.109) \omega \\
\omega & =\frac{8.0}{0.109}=73.3 \frac{\text { rad }}{5}
\end{aligned}
$
The bowling ball is a solid sphere. The moment of inertia of a solid sphere is:
$
\begin{aligned}
& I=\frac{2}{5} m r^2 \\
& I=\left(\frac{2}{5}\right)(7.25)(0.109)^2 \\
& I=0.0345 \mathrm{~kg} \cdot \mathrm{m}^2
\end{aligned}
$
To find the rotational kinetic energy, we plug these numbers into the equation:
$
\begin{aligned}
& K_r=\frac{1}{2} I \omega^2 \\
& K_r=\left(\frac{1}{2}\right)(0.0345)(73.3)^2 \\
& K_r=185.6 \mathrm{~J}
\end{aligned}
$
Escape Velocity
Notes:
If you want to send a rocket or space ship to explore the rest of the solar system or beyond, the rocket needs enough kinetic energy to escape from the force of Earth’s gravity.
To explain the calculation, we measure height from Earth’s surface and use $\overrightarrow{\boldsymbol{g}}=10 \frac{\mathrm{m}}{\mathrm{s}^2}$ for the strength of the gravitational field. However, when we calculate the escape velocity of a rocket, the rocket has to go from the surface of the Earth to a point where $\overrightarrow{\boldsymbol{g}}$ is small enough to be negligible.
We can still use the conservation of energy, but we need to calculate the potential energy that the rocket has based on its distance from the center of the Earth instead of the surface of the Earth. (When the distance from the Earth is great enough, the gravitational potential energy becomes zero, and the rocket has escaped.) Therefore, the spaceship needs to turn kinetic energy into this much potential energy.
To solve this, we need to turn to Newton’s Law of Universal Gravitation. Recall from Universal Gravitation starting on page 365 that:
$
F_g=\frac{G m_1 m_2}{r^2}
$
The potential energy equals the work that gravity could theoretically do on the rocket, based on the force of gravity and the distance to the center of the Earth:
$
W=\overrightarrow{\boldsymbol{F}} \bullet \overrightarrow{\boldsymbol{d}}=F_g h=\left(\frac{G m_1 m_2}{r^2}\right) h
$
Because $h$ is the distance to the center of the Earth, $h=r$ and we can cancel, giving the equation:
$
U_g=\frac{G m_1 m_2}{r}
$
Now, we can use the law of conservation of energy. The kinetic energy that the rocket needs to have at launch needs equals the potential energy that the rocket has due to gravity. Using $m_1$ for the mass of the Earth and $m_2$ for the mass of the spaceship:
$
\begin{aligned}
\text { Before } & =\text { After } \\
T M E_i & =T M E_f \\
K_i & =U_f \\
\frac{1}{2} D R_2 v_e^2 & =\frac{G m_1 m_2}{r} \\
v_e^2 & =\frac{2 G m_E}{r} \\
v_e & =\sqrt{\frac{2 G m_E}{r}}
\end{aligned}
$
Therefore, at the surface of the Earth, where $m_E=5.97 \times 10^{24} \mathrm{~kg}$ and $r=6.37 \times 10^6 \mathrm{~m}$, this gives $v_e=1.12 \times 10^4 \frac{\mathrm{m}}{\mathrm{s}}=11200 \frac{\mathrm{m}}{\mathrm{s}}$. (If you’re curious, this equals just over 25000 miles per hour.)
Sample Problem:
Q: When Apollo 11 went to the moon, the space ship needed to achieve the Earth’s escape velocity of $11200 \frac{\mathrm{m}}{\mathrm{s}}$ to escape Earth’s gravity. What velocity did the spaceship need to achieve in order to escape the moon’s gravity and return to Earth? (I.e., what is the escape velocity on the surface of the moon?)
Answer/Explanation
$
\text { A: } \begin{aligned}
v_e & =\sqrt{\frac{2 G m_{\text {moon }}}{d_{\text {moon }}}} \\
v_e & =\sqrt{\frac{(2)\left(6.67 \times 10^{-11}\right)\left(7.35 \times 10^{22}\right)}{1.74 \times 10^6}} \\
v_e & =2370 \frac{\mathrm{m}}{\mathrm{s}}
\end{aligned}
$
Power
Notes:power: a measure of the rate at which energy is applied or work is done. Power is calculated by dividing work (or energy) by time.
$
P=\frac{W}{t}=\frac{\Delta K+\Delta U}{t}
$
Power is a scalar quantity and is measured in Watts (W).
$
1 \mathrm{~W}=1 \frac{\mathrm{l}}{\mathrm{s}}=1 \frac{\mathrm{N} \cdot \mathrm{m}}{\mathrm{s}}=1 \frac{\mathrm{kg} \cdot \mathrm{m}^2}{\mathrm{~s}^3}
$
Note that utility companies measure energy in kilowatt-hours. This is because $P=\frac{W}{t}$, which means energy $=W=P t$.
Because $1 \mathrm{~kW}=1000 \mathrm{~W}$ and $1 \mathrm{~h}=3600 \mathrm{~s}$, this means $1 \mathrm{kWh}=(1000 \mathrm{~W})(3600 \mathrm{~s})=3600000 \mathrm{~J}$
Because $W=F d$, this means $P=\frac{F d}{t}=F\left(\frac{d}{t}\right)=F v$
Power in Rotational Systems
In a rotational system, the formula for power looks similar to the equation for power in linear systems, with force replaced by torque and linear velocity replaced by angular velocity:

Solving Power Problems
Many power problems require you to calculate the amount of work done or the change in energy, which you should recall is:
$\begin{aligned} W & =F_{11} d & & \text { if the force is caused by linear displacement } \\ \Delta K_t & =\frac{1}{2} m v^2-\frac{1}{2} m v_o^{2 *} & & \text { if the change in energy was caused by a change in } \\ & =\frac{1}{2} m\left(v^2-v_o^2\right) & & \text { velocity } \\ \Delta U_g & =m g h-m g h_o & & \text { if the change in energy was caused by a change in } \\ & =m g \Delta h & & \text { height }\end{aligned}$
Solving Rotational Power Problems
Power is also applicable to rotating systems:
$
\begin{aligned}
W & =\tau \Delta \theta & & \text { if the work is produced by a torque } \\
\Delta K_r & =\frac{1}{2} I \omega^2-\frac{1}{2} I \omega_o^2 & & \text { if the change in energy was caused by a change in } \\
& =\frac{1}{2} I\left(\omega^2-\omega_o^2\right) & & \text { angular velocity }
\end{aligned}
$
Once you have the work or energy, you can plug it in for either $\mathrm{W}, \Delta K$ or $\Delta U$, use the appropriate parts of the formula:
$
P=\frac{W}{t}=\frac{\Delta K+\Delta U}{t}=F v=\tau \omega
$
and solve for the missing variable.
* $K_t$ is translational kinetic energy. This is the only $K$ used in CP 1 and honors physics. The subscript $t$ is used here to distinguish translational kinetic energy from rotational kinetic energy $\left(K_r\right)$, because both are used in AP ${ }^{\oplus}$ Physics.
Sample Problems:
Q: What is the power output of an engine that pulls with a force of 500 . $N$ over a distance of $100 . \mathrm{m}$ in $25 \mathrm{~s}$ ?
Answer/Explanation
Ans:
$
\begin{aligned}
& W=F d=(500)(100)=50000 \mathrm{~J} \\
& \mathrm{P}=\frac{\mathrm{W}}{\mathrm{t}}=\frac{50000}{25}=2000 \mathrm{~W}
\end{aligned}
$