Topics covered in this chapter:
• Force Applied at an Angle
•Ramp Problems
In this chapter you will learn about different kinds of forces and how they relate.
• Force Applied at an Angle, Ramp Problems, and Pulleys & Tension describe some common situations involving forces and how to calculate the forces involved.
• Centripetal Force describes the forces experienced by an object moving in a circle.
• Center of Mass, Rotational Inertia, and Torque describe the relationship between forces and rotation.
Force Applied at an Angle
Notes:
An important property of vectors is that a vector has no effect on a second vector that is perpendicular to it. As we saw with projectiles, this means that the velocity of an object in the horizontal direction has no effect on the velocity of the same object in the vertical direction. This allowed us to solve for the horizontal and vertical velocities as separate problems.
The same is true for forces. If forces are perpendicular to each other, they act independently, and the two can be separated into separate, independent mathematical problems:
In the x-direction: $\quad \overrightarrow{\boldsymbol{F}}_{\text {net }, x}=m \overrightarrow{\boldsymbol{a}}_{\mathrm{x}}$
In the $y$-direction: $\quad \overrightarrow{\boldsymbol{F}}_{\text {net, }, y}=m \overrightarrow{\boldsymbol{a}}_y$
Note that the above is for linear situations. Two-dimensional rotational problems require calculus, and are therefore outside the scope of this course.
For example, if we have the following forces acting on an object:

The net horizontal force $\left(F_{\mathrm{x}}\right)$ would be $18 \mathrm{~N}+(-6 \mathrm{~N})=+12 \mathrm{~N}$, and the net vertical force $\left(F_{\mathrm{y}}\right)$ would be $9 \mathrm{~N}+(-4 \mathrm{~N})=+5 \mathrm{~N}$. The total net force would be the resultant of the net horizontal and net vertical forces:

Using the Pythagorean Theorem:
$
\begin{array}{ll}
a^2+b^2=c^2 & 169=F_{\text {net }}^2 \\
5^2+12^2=F_{\text {net }}^2 & \sqrt{169}=F_{\text {net }}=13 \mathrm{~N}
\end{array}
$
We can get the angle from trigonometry:
$
\begin{aligned}
& \tan \theta=\frac{\text { opposite }}{\text { adjacent }}=\frac{5}{12}=0.417 \\
& \theta=\tan ^{-1}(\tan \theta)=\tan ^{-1}(0.417)=22.6^{\circ}
\end{aligned}
$
(Of course, because you have just figured out the length of the hypotenuse, you could get the same answer by using $\sin ^{-1}$ or $\cos ^{-1}$.)
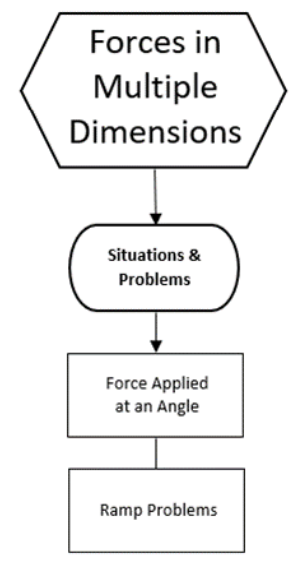
If we have one or more forces that is neither vertical nor horizontal, we can use trigonometry to split the force into a vertical component and a horizontal component.

Recall the following relationships from trigonometry:
Suppose we have a force of $50 \mathrm{~N}$ at a direction of $35^{\circ}$ above the horizontal. In the above diagram, this would mean that $h=50 \mathrm{~N}$ and $\theta=35^{\circ}$ :
The horizontal force is $\overrightarrow{\boldsymbol{F}}_x=h \cos (\theta)=50 \cos \left(35^{\circ}\right)=41.0 \mathrm{~N}$

The vertical force is $\overrightarrow{\boldsymbol{F}}_y=h \sin (\theta)=50 \sin \left(35^{\circ}\right)=28.7 \mathrm{~N}$
Now, suppose that same object was subjected to the same $50 \mathrm{~N}$ force at an angle of $35^{\circ}$ above the horizontal, but also a $20 \mathrm{~N}$ force to the left and a $30 \mathrm{~N}$ force downward.

The net horizontal force would therefore be $41+(-20)=21 \mathrm{~N}$ to the right.
The net vertical force would therefore be $28.7+(-30)=-1.3 \mathrm{~N}$ upwards (which equals $1.3 \mathrm{~N}$ downwards).
Once you have calculated the net vertical and horizontal forces, you can resolve them into a single net force, as in the previous example. (Because the vertical component of the net force is so small, an extra digit is necessary in order to see the difference between the total net force and its horizontal component.)

In some physics problems, a force is applied at an angle but the object can move in only one direction. A common problem is a force applied at an angle to an object resting on a flat surface, which causes the object to move horizontally:
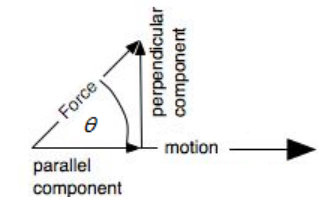
In this situation, only the horizontal (parallel) component of the applied force $\left(F_{\|}\right)$ actually causes the object to move. If magnitude of the total force is $F$, then the horizontal component of the force is given by:
$
F_x=F_{11}=F \cos \theta
$
If the object accelerates horizontally, that means only the horizontal component is causing the acceleration, which means the net force must be $F_{\|}=F \cos \theta$ and we can ignore the vertical component.

For example, suppose the worker in the diagram at the right pushes on the hand truck with a force of $200 \mathrm{~N}$ at an angle of $60^{\circ}$.
The force in the direction of motion (horizontally) would be:
$
\begin{aligned}
F_{11}=F \cos \theta & =200 \cos \left(60^{\circ}\right) \\
& =(200)(0.5)=100 \mathrm{~N}
\end{aligned}
$
In other words, if the worker applies $200 \mathrm{~N}$ of force at an angle of $60^{\circ}$, the resulting horizontal force will be $100 \mathrm{~N}$.
Static Problems Involving Forces at an Angle
Many problems involving forces at an angle are based on an object with no net force (either a stationary object or an object moving at constant velocity) that has three or more forces acting at different angles. In the following diagram, the forces are $\overrightarrow{\boldsymbol{F}}_1$, $\overrightarrow{\boldsymbol{F}}_2$ and $\overrightarrow{\boldsymbol{F}}_3$.
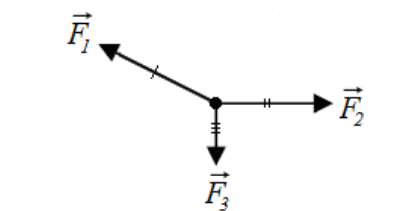
$\overrightarrow{\boldsymbol{F}}_1$ needs to cancel the resultant of $\overrightarrow{\boldsymbol{F}}_2$ and $\overrightarrow{\boldsymbol{F}}_3$ :

Of course, $\overrightarrow{\boldsymbol{F}}_2$ will also cancel the resultant of $\overrightarrow{\boldsymbol{F}}_1$ and $\overrightarrow{\boldsymbol{F}}_3$, and $\overrightarrow{\boldsymbol{F}}_3$ will also cancel the resultant of $\overrightarrow{\boldsymbol{F}}_1$ and $\overrightarrow{\boldsymbol{F}}_2$.
Strategy
1. Resolve all known forces into their horizontal and vertical components.
2. Add the horizontal and vertical components separately.
3. Use the Pythagorean Theorem to find the magnitude of forces that are neither horizontal nor vertical.
4. Because you know the vertical and horizontal components of the resultant force, use arcsine $\left(\sin ^{-1}\right)$, arccosine $\left(\cos ^{-1}\right)$ or $\operatorname{arctangent}\left(\tan ^{-1}\right)$ to find the angle.
Ramp Problems
Notes:
The direction of the normal force does not always directly oppose gravity. For example, if a block is resting on a (frictionless) ramp, the weight of the block is $\overrightarrow{\boldsymbol{F}}_g$, in the direction of gravity. However, the normal force is perpendicular to the ramp, not to gravity.
If we were to add the vectors representing the two forces, we would see that the resultant-the net force-acts down the ramp:
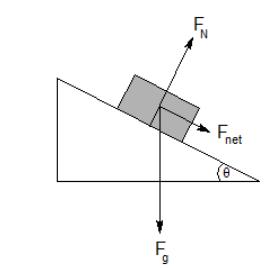
Intuitively, we know that if the ramp is horizontal $(\theta=0)$, the net force is zero and $\overrightarrow{\boldsymbol{F}}_N=\overrightarrow{\boldsymbol{F}}_g$, because they are equal and opposite.
We also know intuitively that if the ramp is vertical $\left(\theta=90^{\circ}\right)$, the net force is $\overrightarrow{\boldsymbol{F}}_g$ and $\overrightarrow{\boldsymbol{F}}_N=0$
If the angle is between 0 and $90^{\circ}$, the net force must be between 0 and $\overrightarrow{\boldsymbol{F}}_g$, and the proportion must be related to the angle (trigonometry!). Note that $\sin \left(0^{\circ}\right)=0$ and $\sin \left(90^{\circ}\right)=1$. Intuitively, it makes sense that the steeper the angle, the greater the net force, and therefore multiplying $\overrightarrow{\boldsymbol{F}}_g$ by the sine of the angle should give the net force down the ramp for any angle between 0 and $90^{\circ}$.
Similarly, If the angle is between 0 and $90^{\circ}$, the normal force must be between $\overrightarrow{\boldsymbol{F}}_g$ (at 0) and $0\left(\right.$ at $\left.90^{\circ}\right)$. Again, the proportion must be related to the angle (trigonometry!). Note that $\cos \left(0^{\circ}\right)=1$ and $\cos \left(90^{\circ}\right)=0$. Intuitively, it makes sense that the shallower the angle, the greater the normal force, and therefore multiplying $\overrightarrow{\boldsymbol{F}}_g$ by the cosine of the angle should give the normal force for any angle 0 and $90^{\circ}$.
Let’s look at a geometric explanation:
From geometry, we can determine that the angle of the ramp, $\theta$, is the same as the angle between gravity and the normal force.
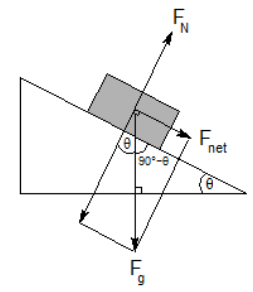
From trigonometry, we can calculate that the component of gravity parallel to the ramp (which equals the net force down the ramp) is the side opposite angle $\theta$. This means:
$
F_{n e t}=F_g \sin \theta
$
The component of gravity perpendicular to the ramp is $F_g \cos \theta$, which means the normal force is:
$
F_N=-F_g \cos \theta
$
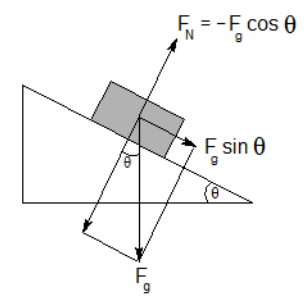
(The negative sign is because the normal force is in the opposite direction from
$
F_g \cos \theta \text {.) }
$
Sample Problem:
Q: A block with a mass of $2.5 \mathrm{~kg}$ sits on a frictionless ramp with an angle of inclination of $35^{\circ}$. How fast does the block accelerate down the ramp?
Answer/Explanation
A: The weight of the block is $F_g=m a=(2.5)(10)=25 \mathrm{~N}$, directed straight down.
However, the net force must be in the same direction as the acceleration.
Therefore, the net force is the component of the force of gravity in the direction that the block can move (down the ramp), which is $F_g \sin \theta$ :
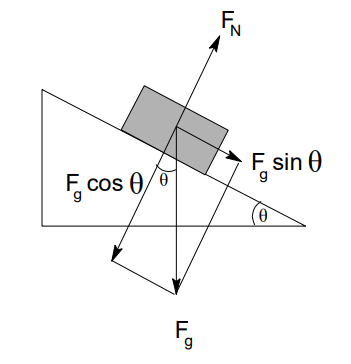
$
F_{\text {net }}=F_g \sin \theta=25 \sin 35^{\circ}=(25)(0.574)=14.3 \mathrm{~N}
$
Now that we know the net force (in the direction of acceleration), we can apply Newton’s Second Law:
$
\begin{aligned}
& F_{\text {net }}=m a \\
& 14.3=2.5 a \\
& a=5.7 \frac{\mathrm{m}}{\mathrm{s}^2}
\end{aligned}
$