Newton’s Laws of Motion
Notes:force: a push or pull on an object.
net force: the amount of force that remains in effect after the effects of opposing forces cancel.
In the MKS system, force is measured in newtons, named after Sir Isaac Newton:
$
\begin{gathered}
1 \mathrm{~N} \equiv 1 \frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}^2} \approx 3.6 \mathrm{oz} \\
4.45 \mathrm{~N} \approx 1 \mathrm{lb} .
\end{gathered}
$
Newton’s First Law: (the law of inertia) Everything keeps doing what it was doing unless a net force acts to change it. “An object at rest remains at rest, unless acted upon by a net force. An object in motion remains in motion, unless acted upon by a net force.”
No net force $\leftrightarrow$ no change in motion (no acceleration).
No net force $\leftrightarrow$ no change in motion (no acceleration).
If an object’s motion is not changing, then there must be no net force on it, which means any
So that’s what forces on it must cancel. inertia means!
For example, a brick sitting on the floor will stay at rest on the floor forever unless an outside force moves it. Wile E. Coyote, on the other hand, remains in motion…

Inertia (resistance to change) is a property of mass. Everything with mass has inertia. The more mass an object has, the more inertia it has.
Newton’s Second Law: Forces cause a change in velocity (acceleration). “A net force, $\overrightarrow{\boldsymbol{F}}$, acting on an object causes the object to accelerate in the direction of the net force.”
Net force $\leftrightarrow$ change in motion (acceleration).
If there is a net force on an object, the object’s motion must change (accelerate), and if an object’s motion has changed, there must have been a net force on it.
In equation form:
$
\overrightarrow{\boldsymbol{a}}=\frac{\overrightarrow{\boldsymbol{F}}_{\mathrm{net}}}{m} \quad \text { or } \quad \overrightarrow{\boldsymbol{F}}_{\text {net }}=m \overrightarrow{\boldsymbol{a}}
$
This equation represents one of the most important relationships in physics.
Newton’s Third Law: Every force produces an equal and opposite reaction force of the same type. The first object exerts a force on the second, which causes the second object to exert the same force back on the first. “For every action, there is an equal and opposite reaction.”
•When you pull on a rope (the action), the rope also pulls on you (the reaction).

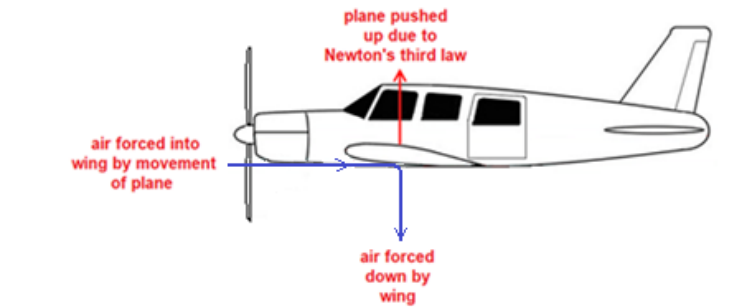
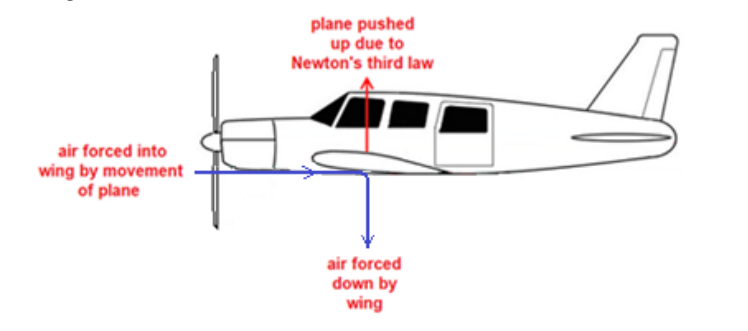
•The wings of an airplane are angled (the “angle of attack”), which deflects air downwards as the plane moves forward. The wing pushing the air down (the action) causes the air to push the wing (and therefore the plane) up (the reaction). This reaction force is called “lift”.
• If you punch a hole in a wall and break your hand, your hand applied a force to the wall (the action). This caused a force from the wall, which broke your hand (the reaction). This may seem obvious, although you will find that someone who has just broken his hand by punching a wall is unlikely to be receptive to a physics lesson!
Systems
system: the collection of objects being considered in a problem.
surroundings: everything that is not part of the system.
For example, gravity is the force of attraction between two objects because of their mass. If a student drops a ball off the roof of the school, the Earth attracts the ball and the ball attracts the Earth. (Because the Earth has a lot more mass than the ball, the ball moves much farther toward the Earth than the Earth moves toward the ball.)
•Ball-Only System: If the system under consideration is only the ball, then the gravity field of the Earth exerts a net force on the ball, causing the ball to move.
• Ball-Earth System: If the system is the ball and the Earth, the force exerted by the Earth on the ball is equal to the force exerted by the ball on the Earth. Because the forces are equal in strength but in opposite directions ( “equal and opposite”), their effects cancel, which means there is no net force on the system. (Yes, there are forces within the system, but that’s not the same thing.) This is why, for example, if all 7.5 billion people on the Earth jumped at once, an observer on the moon would not be able to detect the Earth moving.
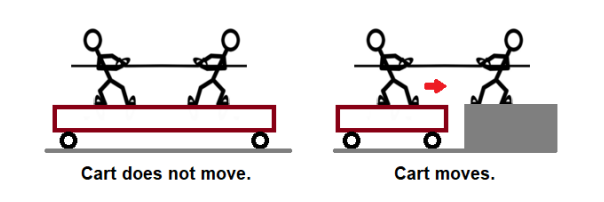
A demonstration of this concept is to have two students standing on a cart (a platform with wheels), playing “tug of war” with a rope. In the student-ropestudent system (or student-rope-student-cart system), the forces within the system cancel. There is no net force (from outside of the system) on the cart, which means the cart does not move. However, if one student moves off the cart (outside of the system), then the student standing on the floor can exert an external net force on the student-cart system, which causes the system (the student and cart) to accelerate.
One of the important implications of this concept is that an object cannot apply a net force to itself. This means that “pulling yourself up by your bootstraps” is impossible according to the laws of physics.
Later, in the section on potential energy on page 377 , we will see that potential energy is a property of systems, and that a single isolated object cannot have potential energy.
Types of Forces
Notes:force: $(\overrightarrow{\boldsymbol{F}}$, vector quantity) a push or pull on an object. 
reaction force: a force that is created in reaction to the action of another force, as described by Newton’s Third Law. Examples include friction and the normal force. Tension is both an applied force and a reaction force.
opposing force: a force in the opposite direction of another force, which reduces the effect of the original force. Examples include friction, the normal force, and the spring force (the force exerted by a spring).
contact force: a force that is caused directly by the action of another force, and exists only while the objects are in contact and the other force is in effect. Contact forces are generally reaction forces and also opposing forces. Examples include friction and the normal force.
net force: the amount of force that remains on an object after the effects of all opposing forces cancel.
An object can have several forces acting on it at once:
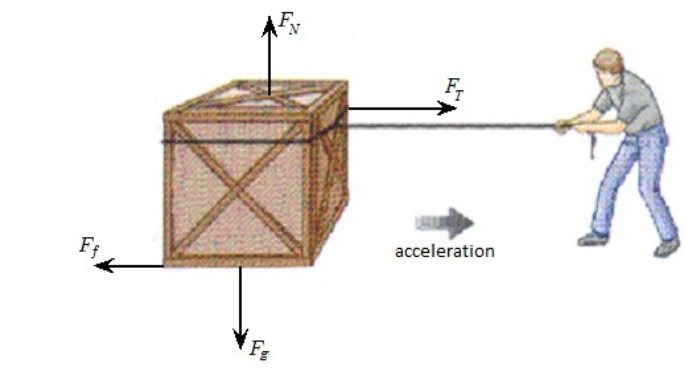
On the box in the above diagram, the forces are gravity $\left(\overrightarrow{\boldsymbol{F}}_{\mathrm{g}}\right)$, the normal force $\left(\overrightarrow{\boldsymbol{F}}_{\mathrm{N}}\right)$, the tension in the rope $\left(\overrightarrow{\boldsymbol{F}}_{\mathrm{T}}\right)$, and friction $\left(\overrightarrow{\boldsymbol{F}}_{\mathrm{f}}\right)$. Notice that in this problem, the arrow for tension is longer than the arrow for friction, because the force of tension is stronger than the force of friction.
net force: the amount of force that remains on an object after the effects of all opposing forces cancel.
You can think of forces as the participants in a tug-of-war:

The net force is the amount of force that is not canceled by the other forces. It determines which direction the object will move, and with how much force.
In the situation with the box above (after canceling out gravity and the normal force, and subtracting friction from the tension) the net force would be:
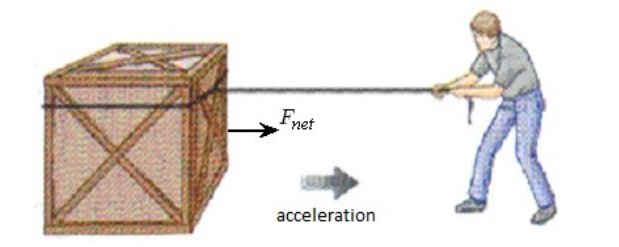
Because there is a net force to the right, the box will accelerate to the right as a result of the force.
Forces are what cause acceleration. If a net force acts on an object, the object will speed up, slow down or change direction. Remember that if the object’s velocity is not changing, there is no net force, which means all of the forces on the object must cancel.
Physics problems are sometimes classified in the following categories:
statics: situations in which there is no net force on an object. (I.e., the object is not accelerating.)
dynamics: situations in which there is a net force on an object. (l.e., the object is accelerating.)
In the MKS system, the unit of force is the newton (N). One newton is defined as the amount of force that it would take to cause a $1 \mathrm{~kg}$ object to accelerate at a rate of $1 \frac{\mathrm{m}}{\mathrm{s}^2}$
$
1 \mathrm{~N} \equiv 1 \frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}^2}
$
Because the acceleration due to gravity on Earth is approximately $10 \frac{\mathrm{m}}{\mathrm{s}^2}, \overrightarrow{\boldsymbol{F}}=m \overrightarrow{\boldsymbol{a}}$ becomes $\overrightarrow{\boldsymbol{F}}_g=m \overrightarrow{\boldsymbol{g}}$, which indicates that a $1 \mathrm{~kg}$ mass on Earth has a weight of approximately $10 \mathrm{~N}$.
In more familiar units, one newton is approximately 3.6 ounces, which happens to be the weight of an average-sized apple. One pound is approximately $4.5 \mathrm{~N}$.
Types of Forces
Weight $\left(\vec{F}_g\right)$
Weight $\left(\overrightarrow{\boldsymbol{F}}_g, \overrightarrow{\boldsymbol{w}}, m \overrightarrow{\boldsymbol{g}}\right)$ is what we call the action of the gravitational force. It is the downward force on an object that has mass, caused by the gravitational attraction between the object and another massive object, such as the Earth. The direction (assuming Earth) is always toward the center of the Earth.
In physics, we represent weight as the vector $\vec{F}_{\mathrm{g}}$. Note that from Newton’s second law, $\overrightarrow{\boldsymbol{F}}_{\mathrm{g}}=m \overrightarrow{\boldsymbol{g}}$, which means on Earth, $\overrightarrow{\boldsymbol{F}}_{\mathrm{g}}=m(10)$. The unit for $\overrightarrow{\boldsymbol{g}}$ is $\frac{\mathrm{N}}{\mathrm{kg}}$.
Normal Force $\left(\vec{F}_N\right)$
The normal force $\left(\vec{F}_N, \vec{N}\right)$ is a force exerted by a surface (such as the ground or a wall) that resists a force exerted on that surface. The normal force is always perpendicular to the surface. (This use of the word “normal” comes from mathematics, and means “perpendicular”.) The normal force is both a contact force and a reaction force.
For example, if you push on a wall with a force of $10 \mathrm{~N}$ and the wall doesn’t move, that means the force you apply causes the wall to apply a normal force of $10 \mathrm{~N}$ pushing back. The normal force is created by your pushing force, and it continues for as long as you continue pushing.

Friction $\left(\vec{F}_f\right)$
Friction $\left(\overrightarrow{\boldsymbol{F}}_f, \overrightarrow{\boldsymbol{f}}\right)$ is a force that opposes sliding (or attempted sliding) of one surface along another. Friction is both a contact force and a reaction force. Friction is always parallel to the interface between the two surfaces.
Friction is caused by the roughness of the materials in contact, deformations in the materials, and/or molecular attraction between materials. Frictional forces are parallel to the plane of contact between two surfaces, and opposite to the direction of motion or applied force. 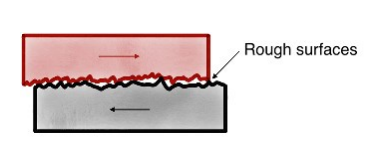
Friction is discussed in more detail in the Friction section, starting on page 286.
Tension $\left(\vec{F}_T\right)$
Tension $\left(\overrightarrow{\boldsymbol{F}}_T, \overrightarrow{\boldsymbol{\tau}}\right)$ is the pulling force on a rope, string, chain, cable, etc. Tension is its own reaction force; tension always applies in both directions at once. The direction of any tension force is along the rope, chain, etc.
For example, in the following picture the person pulls on the rope with a force of $100 \mathrm{~N}$. The rope transmits the force to the wall, which causes a reaction force (also tension) of $100 \mathrm{~N}$ in the opposite direction. The reaction force pulls on the person.
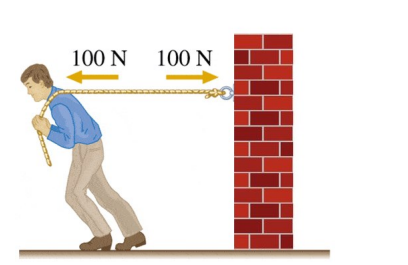
This means that there is a force of $100 \mathrm{~N}$ exerted on the wall by the person (to the left), and a force of $100 \mathrm{~N}$ exerted on the person by the wall (to the right). The two forces cancel, which means there is no net force, and the total tension in the rope adds up to zero.
Thrust $\left(\overrightarrow{\boldsymbol{F}}_t\right)$
Thrust is any kind pushing force, which can be anything from a person pushing on a cart to the engine of an airplane pushing the plane forward. The direction is the direction of the push.
Spring Force $\left(\overrightarrow{\boldsymbol{F}}_s\right)$
The spring force is an elastic force exerted by a spring, elastic (rubber band), etc. The spring force is a reaction force and a restorative force; if you pull or push a spring away from its equilibrium (rest) position, it will exert a force that attempts to return itself to that position. The direction is toward the equilibrium point.
Buoyancy $\left(\vec{F}_b\right)$
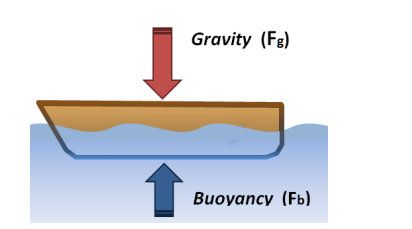
Buoyancy, or the buoyant force, is an upward force exerted by a fluid. The buoyant force causes (or attempts to cause) objects to float. The buoyant force is caused when an object displaces a fluid (pushes it out of the way). This causes the fluid level to rise. Gravity pulls down on the fluid, and the weight of the fluid causes a lifting force on the object. The direction of the buoyant force is always opposite to gravity. Buoyancy is discussed in detail in Physics 2.
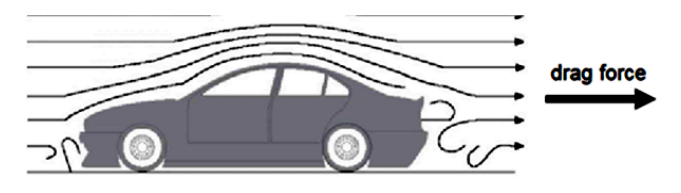
Drag $\left(\overrightarrow{\boldsymbol{F}}_D\right)$
Drag is the opposing force from the particles of a fluid (liquid or gas) as an object moves through it. Drag is similar to friction; it is a contact force and a reaction force because it is caused by the relative motion of the object through the fluid, and it opposes the motion of the object. The direction is therefore opposite to the direction of motion of the object relative to the fluid. An object at rest does not push through any particles and therefore does not create drag.
$\operatorname{Lift}\left(\overrightarrow{\boldsymbol{F}}_L\right)$
Lift is a reaction force caused by an object moving through a fluid at an angle. The object pushes the fluid downward, which causes a reaction force pushing the object upward. The term is most commonly used to describe the upward force on an airplane wing.
Electrostatic Force $\left(\vec{F}_e\right)$
The electrostatic force is a force of attraction or repulsion between objects that have an electrical charge. Like charges repel and opposite charges attract. The electrostatic force is described in more detail in the Introduction:
Magnetic Force $\left(\vec{F}_B\right)$
The magnetic force is a force of attraction or repulsion between objects that have the property of magnetism. Magnetism is caused by the “spin” property of electrons. Like magnetic poles repel and opposite magnetic poles attract.
Magnetism is described in more detail in the Introduction:
Gravitational Fields
Notes:
The gravitational force is an attractive force between objects that have mass. For reasons that are not yet understood, masses exert attraction to each other in proportion to the masses of the objects and in inverse proportion to the square of the distance between them. (This concept will be discussed more fully in the section on Universal Gravitation starting on page 365.)
When considering objects near the Earth’s surface (give or take a few hundred meters) that are small in relation to the size and mass of the Earth, gravity may be considered to be a force field.
force field: a region in which a force acts upon all objects that have some particular characteristic or property.
In the case of gravity, that property is the mass of the object, and the force acts in proportion to the strength of the force field.
Other types of force fields include electric fields, in which an electric force acts on all objects that have electric charge, and magnetic fields, in which a magnetic force acts on all objects that have magnetic susceptibility (the property that causes them to be attracted to or repelled by a magnet).
The strength of a gravitational field is a vector quantity described by the variable $\overrightarrow{\boldsymbol{g}}$ and is equal to the acceleration that the field causes on an object, in proportion to the object’s mass:
$
\overrightarrow{\boldsymbol{g}}=\frac{\overrightarrow{\boldsymbol{F}}_g}{m} \quad \text { which can be rearranged to: } \quad \overrightarrow{\boldsymbol{F}}_g=m \overrightarrow{\boldsymbol{g}}
$
The value of $\overrightarrow{\boldsymbol{g}}$ depends on the mass of the object causing the field (usually the Earth) and the distance to its center of mass (usually the radius of the Earth).
The direction of $\overrightarrow{\boldsymbol{g}}$ is always toward the center of mass of the large object (i.e., usually toward the center of the Earth or toward the ground).
$\overrightarrow{\boldsymbol{g}}$ can be expressed in units of $\frac{\mathrm{m}}{\mathrm{s}^2}$ or $\frac{\mathrm{N}}{\mathrm{kg}}$, which are equivalent.
g-Forces
Acceleration is often described in terms of “g-force”. “g-force” represents the acceleration to which an object (usually a person) is subjected as a fraction/multiple of Earth’s gravity. A force of $1 \mathrm{~g}$ is equivalent to the $10 \frac{\mathrm{N}}{\mathrm{kg}} \equiv 10 \frac{\mathrm{m}}{\mathrm{s}}$ that would apply to an object in free fall near the surface of the Earth.
frame of reference: an arbitrary coördinate system that is used to measure the position and movement of objects. The frame of reference may be stationary or it may be moving in any way (with our without acceleration).
principle of relativity: there is no experiment that can determine whether you are at rest or moving at a constant velocity.
Newton’s second law tells us that forces cause acceleration, and that if an object is not accelerating, then there must be no net force on it. Forces are the only way an object (including a person) can detect its own motion, which means that if there are no forces on an object, all we can tell from within the object’s frame of reference is that the object is either at rest or moving at constant velocity.
Free-Body Diagrams
Notes:
free-body diagram (force diagram): a diagram representing all of the forces acting on an object.
In a free-body diagram, we represent the object as a dot, and each force as an arrow. The direction of the arrow represents the direction of the force, and the relative lengths of the arrows represent the relative magnitudes of the forces.
Consider the following situation:
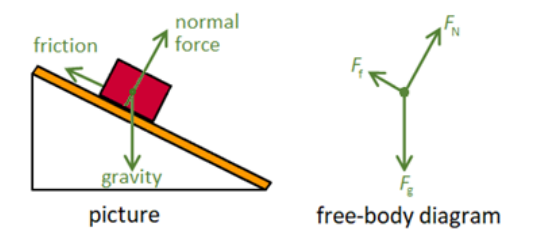
In the picture, a block is sitting on a ramp. The forces on the block are gravity (straight down), the normal force (perpendicular to and away from the ramp), and friction (parallel to the ramp).
In the free-body diagram, the block is represented by a dot. The forces, represented by arrows, are gravity $\left(F_{\mathrm{g}}\right)$, the normal force $\left(F_{\mathrm{N}}\right)$, and friction $\left(F_{\mathrm{f}}\right)$.
Now consider the following situation of a box that accelerates to the right as it is pulled across the floor by a rope:
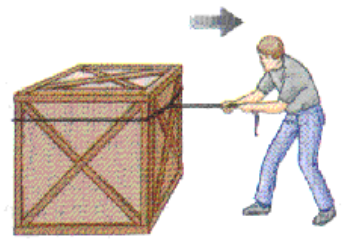
From the picture and description, we can assume that:
• The box has weight, which means gravity is pulling down on it.
• The floor is holding up the box.
• The rope is pulling on the box.
• Friction between the box and the floor is resisting the force from the rope.
• Because the box is accelerating to the right, the force applied by the rope must be stronger than the force from friction.
In the free-body diagram for the accelerating box, we again represent the object (the box) as a dot, and the forces (vectors) as arrows. Because there is a net force, we should also include a legend that shows which direction is positive.
The forces are:
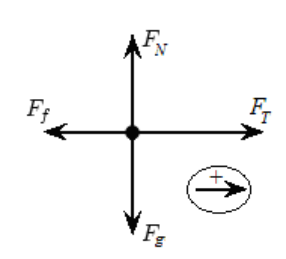
• $\overrightarrow{\boldsymbol{F}}_{\mathrm{g}}=$ the force of gravity pulling down on the box
• $\overrightarrow{\boldsymbol{F}}_{\mathrm{N}}=$ the normal force (the floor holding the box up)
• $\overrightarrow{\boldsymbol{F}}_{\mathrm{T}}=$ the force of tension from the rope. (This might also be designated $\overrightarrow{\boldsymbol{F}}_{\mathrm{a}}$ because it is the force applied to the object.)
• $\overrightarrow{\boldsymbol{F}}_{\mathrm{f}}=$ the force of friction resisting the motion of the box.
Notice that the arrows for the normal force and gravity are equal in length, because in this problem, these two forces are equal in magnitude.
Notice that the arrow for friction is shorter than the arrow for tension, because in this problem the tension is stronger than the force of friction. The difference between the lengths of these two vectors would be the net force, which is what causes the box to accelerate to the right.
In general, if the object is moving, it is easiest to choose the positive direction to be the direction of motion. In our free-body diagram, the legend in the bottom right corner of the diagram shows an arrow with a ” + ” sign, meaning that we have chosen to make the positive direction to the right.
If you have multiple forces in the same direction, each force vector must originate from the point that represents the object, and must be as close as is practical to the exact direction of the force.
For example, consider a rock sitting at the bottom of a pond. The rock has three forces on it: the buoyant force $\left(\overrightarrow{\boldsymbol{F}}_b\right)$ and the normal force $\left(\overrightarrow{\boldsymbol{F}}_N\right)$, both acting upwards, and gravity $\left(\overrightarrow{\boldsymbol{F}}_g\right)$ acting downwards.
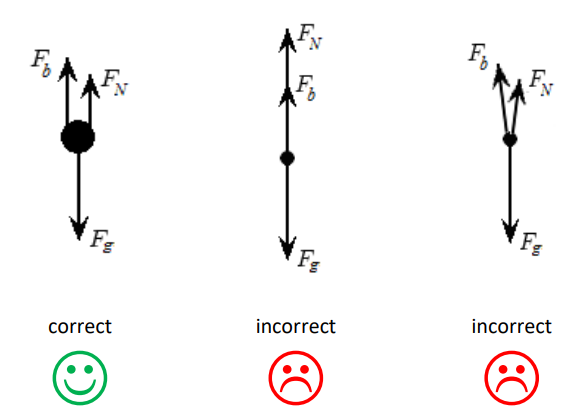
The first representation is correct because all forces originate from the dot that represents the object, the directions represent the exact directions of the forces, and the length of each is proportional to its strength.
The second representation is incorrect because it is unclear whether $\overrightarrow{\boldsymbol{F}}_N$ starts from the object (the dot), or from the tip of the $\overrightarrow{\boldsymbol{F}}_b$ arrow.
The third representation is incorrect because it implies that $\overrightarrow{\boldsymbol{F}}_b$ and $\overrightarrow{\boldsymbol{F}}_N$ each have a slight horizontal component, which is not true.
Because there is no net force (the rock is just sitting on the bottom of the pond), the forces must all cancel. This means that the lengths of the arrows for $\overrightarrow{\boldsymbol{F}}_b$ and $\overrightarrow{\boldsymbol{F}}_N$ need to add up to the length of the arrow for $\overrightarrow{\boldsymbol{F}}_g$.
Steps for Drawing Free-Body Diagrams
In general, the following are the steps for drawing most free-body diagrams.
1. Is gravity involved? (In most physics problems that take place on Earth near the planet’s surface, the answer is yes.)
• Represent gravity as $\overrightarrow{\boldsymbol{F}}_{\mathrm{g}}$ pointing straight down.
2. Is something holding the object up?
• If it is a flat surface, it is the normal force $\left(\vec{F}_{\mathrm{N}}\right)$, perpendicular to the surface.
• If it is a rope, chain, etc., it is the force of tension $\left(\overrightarrow{\boldsymbol{F}}_{\mathrm{T}}\right)$ acting along the rope, chain, etc.
3. Is there a force pulling or pushing on the object?
•If the pulling force involves a rope, chain, etc., the force is tension $\left(\overrightarrow{\boldsymbol{F}}_{\mathrm{T}}\right)$ and the direction is along the rope, chain, etc.
•A pushing force is called thrust $\left(\overrightarrow{\boldsymbol{F}}_{\mathrm{t}}\right)$.
•Only include forces that are acting currently. (Do not include forces that acted in the past but are no longer present.)
4. Is there friction?
• If there are two surfaces in contact, there is almost always friction $\left(\overrightarrow{\boldsymbol{F}}_f\right)$, unless the problem specifically states that the surfaces are frictionless. (In physics problems, ice is almost always assumed to be frictionless.)
• At low velocities, air resistance is very small and can usually be ignored unless the problem explicitly states otherwise.
• Usually, all sources of friction are shown as one combined force. E.g., if there is sliding friction along the ground and also air resistance, the $\overrightarrow{\boldsymbol{F}}_{\mathrm{f}}$ vector includes both.
5. Do we need to choose positive \& negative directions?
• If the problem requires calculations involving opposing forces, you need to indicate which direction is positive. If the problem does not require calculations or if there is no net force, you do not need to do so.
Newton’s Second Law
Notes:
Newton’s Second Law: Forces cause acceleration (a change in velocity). “A net force, $\overrightarrow{\boldsymbol{F}}$, acting on an object causes the object to accelerate in the direction of the net force.”
If there is a net force, the object accelerates (its velocity changes). If there is no net force, the object’s velocity remains the same.
If an object accelerates (its velocity changes), there was a net force on it. If an object’s velocity remains the same, there was no net force on it.
Remember that forces are vectors. “No net force” can either mean that there are no forces at all, or it can mean that there are equal forces in opposite directions and their effects cancel.
static equilibrium: when all of the forces on an object cancel each other’s effects (resulting in a net force of zero) and the object remains stationary.
dynamic equilibrium: when all of the forces on an object cancel each other’s effects (resulting in a net force of zero) and the object remains in motion with constant velocity.
In equation form:
$
\overrightarrow{\boldsymbol{a}}=\frac{\overrightarrow{\boldsymbol{F}}_{\text {net }}}{m} \quad \text { or } \quad \overrightarrow{\boldsymbol{F}}_{\text {net }}=m \overrightarrow{\boldsymbol{a}}
$
The first form is preferred for teaching purposes, because acceleration is what results from a force applied to a mass. (I.e., force and mass are the independent variables and acceleration is the dependent variable. Forces cause acceleration, not the other way around.) However, the equation is more commonly written in the second form, which makes the typesetting and the algebra easier.
Sample Problems
Most of the physics problems involving forces require the application of Newton’s Second Law, $\overrightarrow{\boldsymbol{r}}_{\text {net }}=m \overrightarrow{\boldsymbol{a}}$.
Q: A net force of $50 \mathrm{~N}$ in the positive direction is applied to a cart that has a mass of $35 \mathrm{~kg}$. How fast does the cart accelerate?
Answer/Explanation
A: Applying Newton’s Second Law:
$
\begin{aligned}
\overrightarrow{\boldsymbol{F}}_{\text {net }} & =m \overrightarrow{\boldsymbol{a}} \\
\vec{a} & =\frac{\vec{F}_{n e t}}{m}=\frac{50}{35}=1.43 \frac{\mathrm{m}}{\mathrm{s}^2}
\end{aligned}
$
Q: What is the weight of (i.e., the force of gravity acting on) a $7 \mathrm{~kg}$ block?
A: $\overrightarrow{\boldsymbol{a}}=\overrightarrow{\boldsymbol{g}}$ (because we use the variable $\overrightarrow{\boldsymbol{g}}$ instead of $\overrightarrow{\boldsymbol{a}}$ when the acceleration is caused by a gravity field.)
$
\overrightarrow{\boldsymbol{F}}_g=m \overrightarrow{\boldsymbol{a}}=m \overrightarrow{\boldsymbol{g}}=(7)(10)=70 \mathrm{~N}
$

Q: Two children are fighting over a toy.
Jamie pulls to the left with a force of $40 \mathrm{~N}$, and Edward pulls to the right with a force of $60 \mathrm{~N}$. If the toy has a mass of $0.6 \mathrm{~kg}$, what is the resulting acceleration of the toy?
A: The free-body diagram looks like this:

(We chose the positive direction to the right because it makes more intuitive sense for the positive direction to be the direction that the toy will move.)
$
\begin{aligned}
\overrightarrow{\boldsymbol{F}}_{\text {net }} & =m \overrightarrow{\boldsymbol{a}} \\
\overrightarrow{\boldsymbol{a}} & =\frac{\overrightarrow{\boldsymbol{F}}_{\text {net }}}{m}=\frac{-40+60}{0.6}=\frac{+20}{0.6}=+33.3 \frac{\mathrm{m}}{\mathrm{s}^2} \text { (to the right) }
\end{aligned}
$
Q: A person applies a net force of $100 . N$ to cart full of books that has a mass of $75 \mathrm{~kg}$. If the cart starts from rest, how far will the cart have moved by the time it gets to a speed of $4.0 \frac{\mathrm{m}}{\mathrm{s}}$ ?
A: We are looking for $\overrightarrow{\boldsymbol{d}}$ (“how far”), so this is ultimately a motion problem. Of the variables used in motion problems, we have $\overrightarrow{\boldsymbol{v}}_o=0$ (starts from rest) and $\vec{v}=3.0 \frac{\mathrm{m}}{\mathrm{s}}$. We don’t have all of the variables for any of the equations. The closest we have is 2 out of the 3 variables we need for $\overrightarrow{\boldsymbol{v}}^2-\overrightarrow{\boldsymbol{v}}_o^2=2 \overrightarrow{\boldsymbol{a}} \overrightarrow{\boldsymbol{d}}$. Substituting gives us:
$
\begin{aligned}
\overrightarrow{\boldsymbol{v}}^2-\overrightarrow{\boldsymbol{v}}_o^2 & =2 \overrightarrow{\boldsymbol{a}} \overrightarrow{\boldsymbol{d}} \\
\overrightarrow{\boldsymbol{d}} & =\frac{\overrightarrow{\boldsymbol{v}}^2-\overrightarrow{\boldsymbol{v}}_o^2}{2 \overrightarrow{\boldsymbol{a}}}=\frac{4^2-0^2}{2 \overrightarrow{\boldsymbol{a}}}=\frac{16}{2 \overrightarrow{\boldsymbol{a}}}=\frac{8}{\overrightarrow{\boldsymbol{a}}}
\end{aligned}
$
To progress farther, we need the acceleration. We have $\overrightarrow{\boldsymbol{F}}_{\text {net }}$ and $m$, so we can use Newton’s $2^{\text {nd }}$ Law:
$
\begin{aligned}
\overrightarrow{\boldsymbol{F}}_{\text {net }} & =m \overrightarrow{\boldsymbol{a}} \\
\overrightarrow{\boldsymbol{a}} & =\frac{\overrightarrow{\boldsymbol{F}}_{n e t}}{m}=\frac{100}{75}=1 . \overline{3} \frac{\mathrm{m}}{\mathrm{s}^2}
\end{aligned}
$
We can now substitute this value into the equation above, giving:
$
\vec{d}=\frac{8}{\vec{a}}=\frac{8}{1 . \overline{3}}=6.0 \mathrm{~m}
$
Tension
Notes:
tension $\left(\overrightarrow{\boldsymbol{F}}_T, \overrightarrow{\boldsymbol{T}}\right)$ : the pulling force on a rope, string, chain, cable, etc.
Tension is its own reaction force; tension always travels through the rope in both directions at once, and unless there are additional forces between one end of the rope and the other, the tension at every point along the rope is the same. The direction of tension is always along the rope.
For example, in the following picture a blindfolded person pulls on a rope with a force of $100 \mathrm{~N}$. The rope transmits the force to the scale, which transmits the force to the other rope and then to the wall. This causes a reaction force (also tension) of $100 \mathrm{~N}$ in the opposite direction.
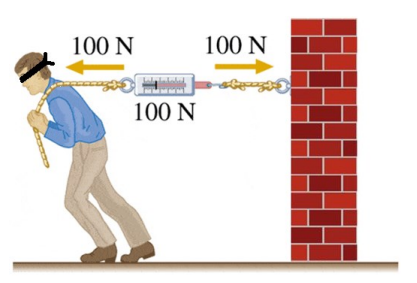
The scale attached to the rope
measures $100 \mathrm{~N}$, because that is the amount of force (tension) that is stretching the spring in the scale.
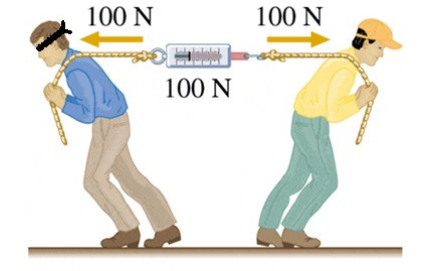
If we replace the brick wall with a person who is pulling with a force of $100 \mathrm{~N}$, the blindfolded person has no idea whether the $100 \mathrm{~N}$ of resistance is coming from a brick wall or another person. Thus, the forces acting on the blindfolded person (and the scale) are the same.
Of course, the scale doesn’t “know” either, so it still reads $100 \mathrm{~N}$.
Pulleys
pulley: a wheel used to change the direction of tension on a rope
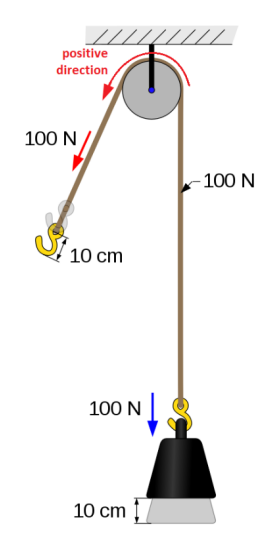
The tension remains the same in all parts of the rope.
In the example at the right (with one pulley), it takes $100 \mathrm{~N}$ of force to lift a $100 \mathrm{~N}$ weight. The pulley changes the direction of the force, but the amount of force does not change. If the rope is pulled $10 \mathrm{~cm}$, the weight is lifted by the same $10 \mathrm{~cm}$.
Up to this point, we have chosen a single direction (left/right or up/down) to be the positive direction. With pulleys, we usually define the positive and negative directions to follow the rope. In this example, we would most likely choose the positive direction to be the direction that the rope is pulled. Instead of saying that positive is upward for the weight and downward for the hook, we would usually say that the positive direction is counter-clockwise $(U)$, because that is the direction that the pulley will turn.
Mechanical Advantage
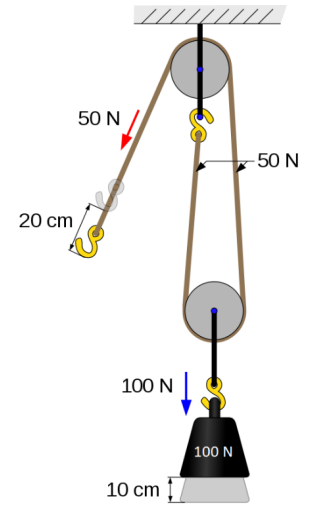
If we place a second pulley just above the weight that we want to lift, two things will happen when we pull on the rope:
1. As we pull on the rope, there is less rope between the two pulleys. This means the lower pulley will move upward.
2. Both of the sections of rope that go around the lower pulley will be lifting the $100 \mathrm{~N}$ weight. This means each side will hold half of the weight $(50 \mathrm{~N})$. Therefore, the tension in every part of the rope is $50 \mathrm{~N}$, which means it takes half as much force to lift the weight.
3. The length of rope that is pulled is divided between the two sections that go around the lower pulley. This means that pulling the rope $20 \mathrm{~cm}$ will raise the weight half as much $(10 \mathrm{~cm})$.
Notice that when the force is cut in half, the length of rope is doubled. The double pulley is effectively trading force for distance. Later, in the Introduction: Energy, Work \& Power unit starting on page 371 , we will see that force times distance is work (change in energy). This means using half as much force but pulling the rope twice as much distance takes the same amount of energy to lift the weight.
As you would expect, as we add more pulleys, the force needed is reduced and the distance increases. This reduction in force is called mechanical advantage.
mechanical advantage: the ratio of the force applied by a machine divided by the force needed to operate it.
The mechanical advantage is equal to the number of ropes supporting the hanging weight, and therefore also equal to the number of pulleys.
The mechanical advantage of the above system is 2.
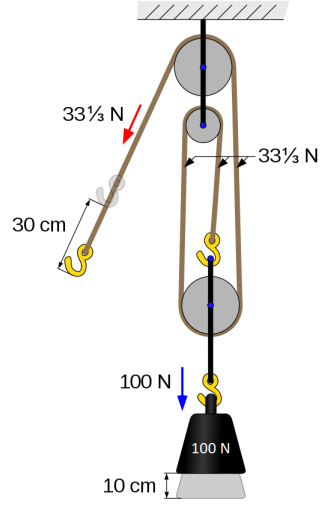
If we add a third pulley, we can see that there are now three sections of the rope that are lifting the $100 \mathrm{~N}$ weight. This means that each section is holding up $1 / 3$ of the weight. This means that the tension in the rope is $1 / 3$ of $100 \mathrm{~N}$, or $33 \frac{1}{3} \mathrm{~N}$, but we now need to pull three times as much rope to lift the weight the same distance.
A two-pulley system has a mechanical advantage of 2 , because it applies twice as much force to the weight as you need to apply to the rope. Similarly, a 3-pulley system has a mechanical advantage of 3 , and so on.
The mechanical advantage of any pulley system equals the number of ropes participating in the lifting.
block and tackle: a system of two or more
pulleys (which therefore have a mechanical advantage of 2 or more) used for lifting heavy loads.
Atwood’s Machine
Atwood’s machine is named for the English mathematician George Atwood. The machine is a device with a single pulley in which one weight, which is pulled down by gravity, is used to lift a second weight. Atwood invented the machine in 1784 to verify Isaac Newton’s equations of motion with constant acceleration.
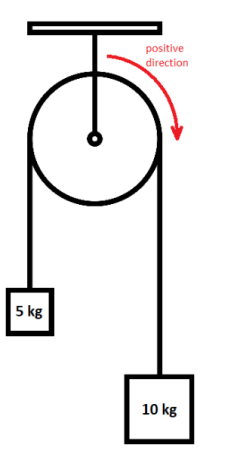
To illustrate how Atwood’s experiment works, consider the system to the right. To simplify the problem, we will assume that the pulley has negligible mass and operates with no friction. Let us choose the positive direction as the direction that turns the pulley clockwise $(\mathrm{U})$. We could have chosen either direction to be positive, but it makes intuitive sense to choose the direction that the system will move when we release the weights.
The force on the mass on the right is its weight, which is $m \overrightarrow{\boldsymbol{g}}=(10)(+10)=100 \mathrm{~N}$. (We use a positive number for acceleration because gravity is attempting to accelerate this weight in the positive direction.)
The force on the mass on the left is $m \overrightarrow{\boldsymbol{g}}=(5)(-10)=-50 \mathrm{~N}$. The acceleration is negative because gravity is pulling this weight in the negative direction.
The net force on the system is therefore $\overrightarrow{\boldsymbol{F}}_{\text {net }}=\sum \overrightarrow{\boldsymbol{F}}=100+(-50)=50 \mathrm{~N}$.
The masses are connected by a rope, which means both masses will accelerate together. The total mass is $15 \mathrm{~kg}$.
Newton’s Second Law says:
$
\begin{aligned}
\overrightarrow{\boldsymbol{F}}_{n e t} & =m \overrightarrow{\boldsymbol{a}} \\
+50 & =15 \overrightarrow{\boldsymbol{a}} \\
\overrightarrow{\boldsymbol{a}} & =\frac{50}{15}=+3 . \overline{3} \frac{\mathrm{m}}{\mathrm{s}^2}
\end{aligned}
$
I.e., the system will accelerate at $3.3 \frac{\mathrm{m}}{\mathrm{s}^2}$ in the positive direction (clockwise).
Atwood performed experiments with different masses and observed behavior that was consistent with both Newton’s second law, and with Newton’s equations of motion.
Notice that the solution to finding acceleration in a problem involving Atwood’s machine is to simply find the net force, add up the total mass, and use $\overrightarrow{\boldsymbol{F}}_{\text {net }}=m \overrightarrow{\boldsymbol{a}}$.
An important feature of Newton’s second law is that it can be applied to an entire system, or to any component of the system.
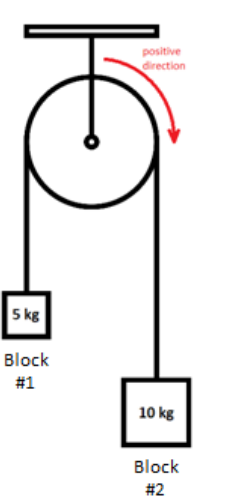
For the Atwood’s machine pictured, we found that:
Entire system:
$
\begin{aligned}
\overrightarrow{\boldsymbol{F}}_{\text {net }} & =m \overrightarrow{\boldsymbol{a}} \\
+50 \mathrm{~N} & =(5 \mathrm{~kg}+10 \mathrm{~kg})\left(3 . \overline{3} \frac{\mathrm{m}}{\mathrm{s}^2}\right)
\end{aligned}
$
We can apply Newton’s second law to each block separately:
$
\begin{aligned}
& \overrightarrow{\boldsymbol{F}}_{1, n e t}=m_1 \overrightarrow{\boldsymbol{a}} \\
& \overrightarrow{\boldsymbol{F}}_{2, n e t}=m_2 \overrightarrow{\boldsymbol{a}}
\end{aligned}
$
Because the blocks are connected via the same rope, the acceleration is the same for both blocks.
This means that we can apply Newton’s second law to either of the blocks to determine the tension in the rope:
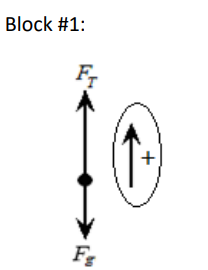
$\begin{gathered}\overrightarrow{\boldsymbol{F}}_{1, \text { net }}=\left(\overrightarrow{\boldsymbol{F}}_T-\overrightarrow{\boldsymbol{F}}_{g, 1}\right) \quad \overrightarrow{\boldsymbol{F}}_{1, \text { net }}=m_1 \overrightarrow{\boldsymbol{a}} \\ \left(\overrightarrow{\boldsymbol{F}}_T-m_1 \overrightarrow{\boldsymbol{g}}\right)=m_1 \overrightarrow{\boldsymbol{a}} \\ {\left[\overrightarrow{\boldsymbol{F}}_T-(5)(10)\right]=(5)(3 . \overline{3})} \\ \overrightarrow{\boldsymbol{F}}_T-(-50)=16 . \overline{6} \\ \overrightarrow{\boldsymbol{F}}_T=66 . \overline{6} \mathrm{~N}\end{gathered}$
Block \#2: (same calculation; yields same result)
We can do the same calculation for Block \#2, with the same result for $\overrightarrow{\boldsymbol{F}}_T$. (Remember that we chose the positive direction to be the direction that the system moves. This means the positive direction is up for block \#1, but down for block \#2.)
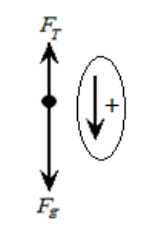
$\begin{gathered}\overrightarrow{\boldsymbol{F}}_{2, n e t}=\left(\overrightarrow{\boldsymbol{F}}_{g, 2}-\overrightarrow{\boldsymbol{F}}_T\right) \quad \overrightarrow{\boldsymbol{F}}_{2, \text { et }}=m_2 \overrightarrow{\boldsymbol{a}} \\ \left(m_2 \overrightarrow{\boldsymbol{g}}-\overrightarrow{\boldsymbol{F}}_T\right)=m_2 \overrightarrow{\boldsymbol{a}} \\ {\left[(10)(10)-\overrightarrow{\boldsymbol{F}}_T\right]=(10)(3 . \overline{3})} \\ 100-\overrightarrow{\boldsymbol{F}}_T=33 . \overline{3} \\ \overrightarrow{\boldsymbol{F}}_T=66 . \overline{6} \mathrm{~N} \\ \text { Q.E.D. }\end{gathered}$
A variation of Atwood’s machine is to have one of the masses on a horizontal table (possibly on a cart to reduce friction). This means that the net force is only the action of gravity on the hanging mass.
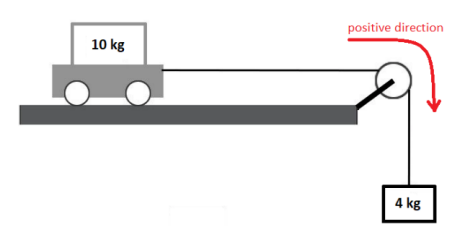
Consider the problem illustrated to the right. To simplify the problem, we will assume that the pulley has negligible mass, and that both the pulley and the cart are frictionless. The $10 \mathrm{~kg}$ for the mass on the left includes the mass of the cart.
The forces on the two masses are:
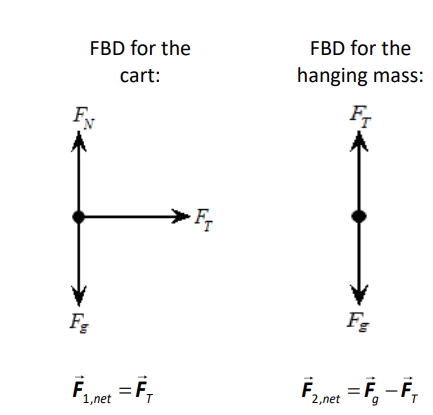
Gravity and the normal force cancel for the cart. The tensions cancel because they are equal (it’s the same rope) and are in opposite directions. This means that the only uncancelled force is the force of gravity on the $4 \mathrm{~kg}$ mass. This uncancelled force is the net force, which is $\overrightarrow{\boldsymbol{F}}_{n e t}=m g=(4)(10)=40 \mathrm{~N}$.
The total mass is $10+4=14 \mathrm{~kg}$.
Now that we have the net force and the total mass, we can find the acceleration using Newton’s Second Law:
$
\begin{aligned}
\overrightarrow{\boldsymbol{F}}_{n e t} & =m \overrightarrow{\boldsymbol{a}} \\
40 & =14 \overrightarrow{\boldsymbol{a}} \\
\overrightarrow{\boldsymbol{a}} & =\frac{40}{14}=2.86 \frac{\mathrm{m}}{\mathrm{s}^2}
\end{aligned}
$
If we also need to find the tension, we can apply Newton’s second law to the cart:
$
\begin{aligned}
& F_{\text {net, }, \text { art }}=F_T \\
& m_{\text {cart }} a=F_T \\
& (10)(2.86)=28.6 \mathrm{~N}
\end{aligned}
$
or we can apply Newton’s second law to the hanging mass:
$
\begin{aligned}
& F_{\text {net, hang }}=F_g-F_T \\
& m_{\text {hang }} a=F_g-F_T \\
& (4)(2.86)=(4)(10)-F_T \\
& 11.4=40-F_T \\
& F_T=40-11.4=28.6 \mathrm{~N}
\end{aligned}
$
Alternative Approach
In most physics textbooks, the solution to Atwood’s machine problems is presented as a system of equations. The strategy is:
– Draw a free-body diagram for each block.
– Apply Newton’s $2^{\text {nd }}$ Law to each block separately, giving $F_{\text {net }}=m_1 a$ for block 1 and $F_{\text {net }}=F_g-F_T=m_2 a$, which becomes $F_{\text {net }}=m_2 g-F_T=m_2 a$ for block 2 .
– Set the two $F_{n e t}$ equations equal to each other, eliminate one of $F_T$ or $a$, and solve for the other.
This is really just a different presentation of the same approach, but most students find it less intuitive.
Friction
Notes:
Most people understand the concept of friction. If you say, “The wheel is too hard to turn because there’s too much friction,” people will know what you mean.
friction: a contact force that resists sliding of surfaces against each other.
Friction is caused by the roughness of the materials in contact, deformations in the materials, and molecular attraction between materials.
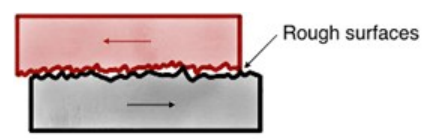
If you slide (or try to slide) the objects in the direction of the arrows, the force you apply would need to be enough to occasionally lift the upper object so that the rough parts of the surfaces have enough room to pass.
Frictional forces are parallel to the plane of contact between two surfaces, and opposite to the direction of motion or applied force.
There are two types of friction:
static friction: friction between surfaces that are not moving relative to each other. Static friction resists the surfaces’ ability to start sliding against each other.
kinetic friction: friction between surfaces that are moving relative to each other. Kinetic friction resists the surfaces’ ability to keep sliding against each other.
Consider the situations below. Suppose that it takes $10 \mathrm{~N}$ of force to overcome static friction and get the box moving. Suppose that once the box is moving, it takes $9 \mathrm{~N}$ of force to keep it moving.
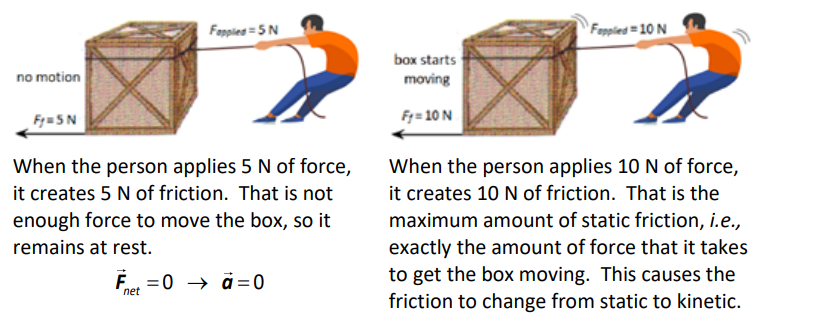
Kinetic Friction
Once the box is moving, the kinetic friction remains constant regardless of the force applied. (Because the person is applying more force than the force of friction, there is a net force to the right, which means the box accelerates to the right.)
Notice that the amount of kinetic friction $(9 \mathrm{~N})$ is less than the maximum static friction $(10 \mathrm{~N})$; it takes more force to start an object moving than to keep it moving.
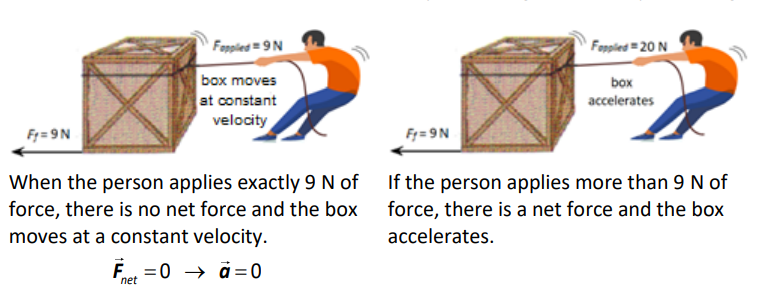
For the above situations, a graph of the applied force vs. friction would look approximately like this:
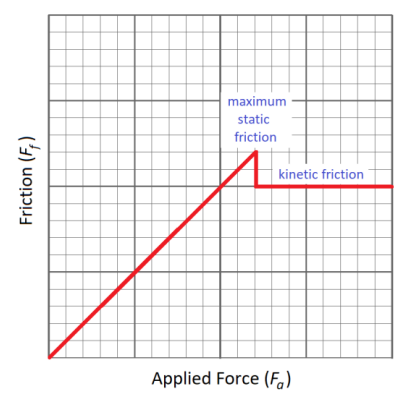
While the object is not moving, the force of friction is always equal to the applied force. As soon as the applied force is enough to start the object moving, the friction changes to kinetic friction. Once the object is moving, any additional applied force does not increase the friction. (Instead, that additional force would cause acceleration.)
The two factors that affect friction are:
•Roughness and other qualities of the surfaces that affect how difficult it is to slide them against each other. This is described by a number called the coëfficient of friction $(\mu)$.
•The amount of force that is pressing the surfaces together. This is, of course, the normal force $\left(\overrightarrow{\boldsymbol{F}}_N\right)$.
coëfficient of friction $(\mu)$ : a material-specific constant that is the ratio of friction to the normal force.
$
\mu=\frac{\overrightarrow{\boldsymbol{F}}_f}{\overrightarrow{\boldsymbol{F}}_N}
$
The coëfficient of friction is a dimensionless number, which means that it has no units. (This is because $\mu$ is a ratio of two forces, which means the units cancel.) The coëfficient of friction takes into account the surface characteristics of the objects in contact. Because static friction and kinetic friction are different situations, their coëfficients of friction are different.
coëfficient of static friction $\left(\mu_s\right)$ : the coëfficient of friction between two surfaces when the surfaces are not moving relative to each other.
coëfficient of kinetic friction $\left(\mu_k\right)$ : the coëfficient of friction between two surfaces when the surfaces are sliding against each other.
The force of friction on an object is given by rearranging the equation for the coëfficient of friction:
$F_f \leq \mu_s F_N \quad$ for an object that is stationary, and
$F_f=\mu_k F_N \quad$ for an object that is moving
Where $F_f$ is the magnitude of the force of friction, $\mu_s$ and $\mu_k$ are the coëfficients of static and kinetic friction, respectively, and $F_N$ is the magnitude of the normal force.
Note that the force of static friction is an inequality. As described above, when an object is at rest the force that resists sliding is, of course, equal to the force applied.
Friction as a Vector Quantity
Like other forces, the force of friction is, of course, actually a vector. Its direction is:
• parallel to the interface between the two surfaces and opposite to the direction of motion (kinetic friction)
• opposite to the component of the applied force that is parallel to the interface between the surfaces (static friction)
Whether the force of friction is positive or negative depends on the above and on which direction you have chosen to be positive. When in doubt, go back to the freebody diagram.
Drag
Notes:
Drag is the force exerted by particles of a fluid” resisting the motion of an object relative to a fluid. The drag force is essentially friction between the object and particles of the fluid.
${ }^*$ A fluid is any substance whose particles can separate easily, allowing it to flow (does not have a definite shape) and allowing objects to pass through it. Fluids can be liquids or gases.
Most of the problems that involve drag fall into three categories:
1. The drag force is small enough that we ignore it.
2. The drag force is equal to some other force that we can measure or calculate.
3. The question asks only for a qualitative comparison of forces with and without drag.
The drag force can be estimated in simple situations, given the velocity, shape, and cross-sectional area of the object and the density of the fluid it is moving through.
For these situations, the drag force is given by the following equation:
$
\overrightarrow{\boldsymbol{F}}_D=-\frac{1}{2} \rho \overrightarrow{\boldsymbol{v}}^2 C_D A
$
where:
where:
$\overrightarrow{\boldsymbol{F}}_0=$ drag force
$\rho=$ density of the fluid that the object is moving through
$\overrightarrow{\boldsymbol{v}}=$ velocity of the object (relative to the fluid)
$C_D=$ drag coëfficient of the object (based on its shape)
$A=$ cross-sectional area of the object in the direction of motion
This equation applies when:
• the object has a blunt form factor
• the object’s velocity relative to the properties of the fluid causes turbulence in the object’s wake
• the fluid is in laminar (not turbulent) flow before it interacts with the object
• the fluid has a relatively low viscosity*
Laminar flow occurs when the velocity of the fluid (or the object moving through it) is relatively low, and the particles of fluid move in a straight line in an organized fashion.
Turbulent flow occurs when the velocity of the fluid (or the object moving through it) is high, and the particles move in a more jumbled, random manner. In general, turbulent flow causes higher drag forces.

“Viscosity is a measure of how “gooey” a fluid is, meaning how much it resists flow and hinders the motion of objects through itself. Water has a low viscosity; honey and ketchup are more viscous.
The drag coëfficient, $C_0$, is a dimensionless number (meaning that it has no units). The drag coëfficient encompasses all of the types of friction associated with drag, including form drag and skin drag. It serves the same purpose in drag problems that the coëfficient of friction $(\mu)$ serves in problems involving friction between solid surfaces.
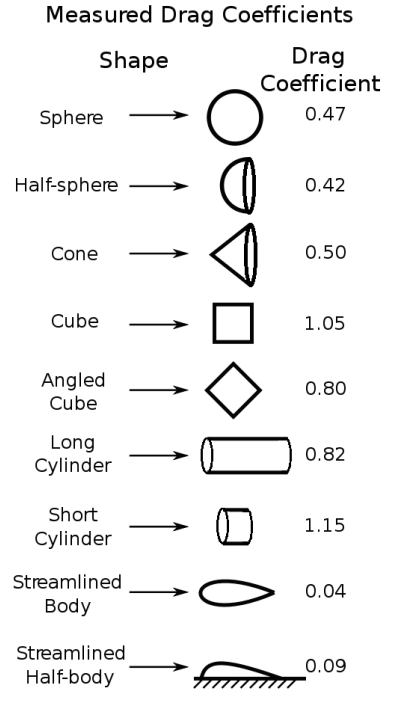
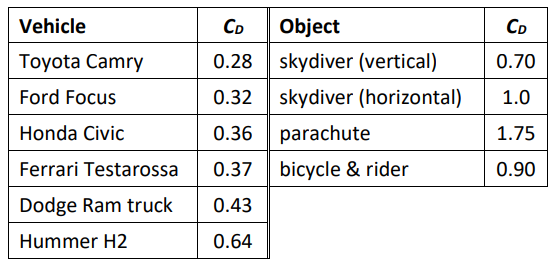
Approximate drag coëfficients for simple shapes are given in the table to the right, assuming that the fluid is moving (relative to the object) in the direction of the arrow.
The reason that raindrops have their characteristic shape (“streamlined body”) is because the drag force changes their shape until they have the shape with the least amount of drag.
The reason that many cars have rooves that slope downward from the front of the car to the back is to reduce the drag force.
Drag coefficients of some vehicles and other objects: