Topics covered in this chapter: 
In this chapter you will learn about different kinds of forces and how they relate.
• Early Theories of the Universe describes the geocentric (Earth-centered) model of the universe, and the theories of Ptolemy and Copernicus.
• Kepler’s Laws of Planetary Motion describes the motion of planets and other celestial bodies and the time period that it takes for planets to revolve around stars throughout the universe.
• Universal Gravitation describes how to calculate the force of mutual gravitational attraction between massive objects such as planets and stars.
Early Theories of the Universe
Notes:
Prior to the renaissance in Europe, most people believed that the Earth was the center of the universe. Early astronomers observed objects moving across the night sky. Objects that were brighter and changed their position significantly from one night to the next were called planets. Objects that were dimmer and more constant (changed their position more gradually from one night to the next) were called stars.
Retrograde Motion and Epicycles
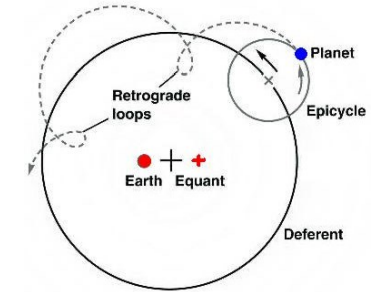
Early astronomers observed that planets sometimes moved “backwards” as they moved across the sky.
retrograde: apparent “backwards” motion of a planet as it appears to move across the sky.
The ancient astronomer Claudius Ptolemy theorized that this retrograde motion was caused by the planets moving in small circles, called epicycles, as they moved in their large circular path around the Earth, called the deferent.
Heliocentric Theory
In 1532, Polish mathematician and astronomer Nicolaus Copernicus published a new heliocentric theory of the universe that placed the sun at the center and designated the Earth as one of the planets that revolve around the sun.
heliocentric theory: the theory that the sun (not the Earth) is the center of the universe.
The assumptions of Copernicus’s theory were:
1. There is no one center of all the celestial circles or spheres.”
2. The center of the Earth is the center towards which heavy objects move’, and the center of the lunar sphere (the moon’s orbit). However, the center of the Earth is not the center of the universe.
3. All the spheres surround the sun as if it were in the middle of them, and therefore the center of the universe is near the sun.
4. The spheres containing the stars are much farther from the sun than the sphere in which the Earth moves. This far-away sphere that contained the stars was called the firmament.
5. The firmament does not move. The stars appear to move because the Earth is rotating.
6. The sun appears to move because of a combination of the Earth rotating and revolving around the sun. This means the Earth is just a planet, and nothing special (as far as the universe is concerned).
7. The apparent motion of the planets (both direct and retrograde) is explained by the Earth’s motion.
${ }^*$ At the time, it was thought that planets and stars were somehow attached to the surface of a hollow sphere, and that they moved along that sphere.
${ }^{\dagger}$ Remember that Copernicus published this theory more than 150 years before Isaac Newton published his theory of gravity.
Kepler’s Laws of Planetary Motion
Notes:
The German mathematician and astronomer Johannes Kepler lived about 100 years after Copernicus. Kepler derived three laws and equations that govern planetary motion, which were published in three volumes between 1617 and 1621 .
Kepler’s First Law
The orbit of a planet is an ellipse, with the sun at one focus.
Kepler’s Second Law
A line that joins a planet with the sun will sweep out equal areas in equal amounts of time.
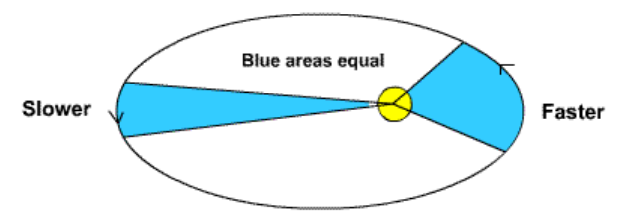
I.e., the planet moves faster as it moves closer to the sun and slows down as it gets farther away. If the planet takes exactly 30 days to sweep out one of the blue areas above, then it will take exactly 30 days to sweep out the other blue area, and any other such area in its orbit.
While we now know that the planet’s change in speed is caused by the force of gravity, Kepler’s Laws were published fifty years before Isaac Newton published his theory of gravity.
Kepler’s Third Law
If $T$ is the period of time that a planet takes to revolve around a sun and $r_{\text {ave. }}$ is the average radius of the planet from the sun (the length of the semi-major axis of its elliptical orbit) then:
$\frac{T^2}{r_{\text {ave. }}^3}=$ constant for every planet in that solar system
We now know that, $\frac{T^2}{r_{\text {ave. }}^3}=\frac{4 \pi^2}{G M}$, where $G$ is the universal gravitational constant and $M$ is the mass of the star in question, which means this ratio is different for every planetary system. For our solar system, the value of $\frac{T^2}{r_{\text {ave. }}^3}$ is approximately $9.5 \times 10^{-27} \frac{\mathrm{s}^2}{\mathrm{~m}^3}$ or $3 \times 10^{-34} \frac{\text { years }}{\mathrm{m}^3}$.
Kepler’s third law allows us to estimate the mass of a planet in some distant solar system, based on the mass of its sun and the time it takes for the planet to make one revolution.
Universal Gravitation
Notes:
Gravity is a force of attraction between two objects because of their mass. The cause of this attraction is not currently known, though the most popular theory is that it is a force mediated by an elementary particle called a graviton.

An object with more mass causes a stronger gravitational force, which means “the more mass you have, the more attractive you are.”
However, the force gets weaker as the object gets farther away
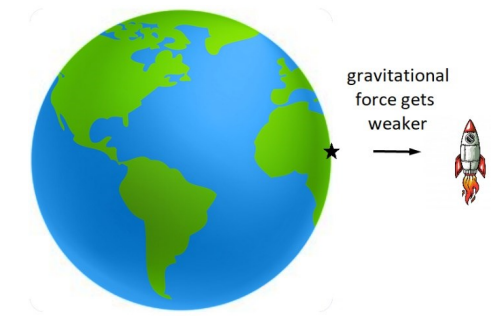
If we are on the Earth, our distance from the part of the Earth that we are standing on is zero, but our distance from the opposite side of the Earth would be the diameter of the Earth, which is about 8 000 miles.
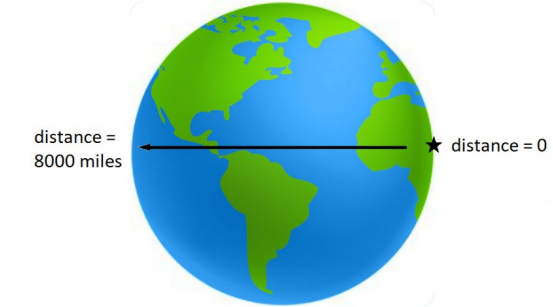
This means that we need to measure distance from the center of mass of the Earth, which is approximately the center of the Earth. If we are on the surface of the Earth, this distance would be the radius of the Earth, which is $6.37 \times 10^6 \mathrm{~m}$ (a little less than 4000 miles).
If we represent the gravitational pull of the Earth as a fraction, it would be proportional to:
$
\frac{\text { mass of Earth }}{\text { distance from center of Earth }}
$
If we write this as an equation, using the mathematical symbol $\propto$, which “is proportional to”, it would look like:
$
F_g \propto \frac{m}{r}
$
However, all objects with mass have gravity. If we have two objects, such as the Earth and the sun, they pull on each other. This means that the total gravitational pull between the Earth and the sun would be:
$
\left(\frac{\text { mass of sun }}{\text { distance from the sun }}\right) \cdot\left(\frac{\text { mass of Earth }}{\text { distance from the Earth }}\right)
$
If we call the sun \#1 and the Earth \#2, this would give us:
$
F_g \propto \frac{m_1}{r_1} \cdot \frac{m_2}{r_2}
$
However, because the distance from the sun to the Earth is the same as the distance from the Earth to the sun, $r_1=r_2=r$, which means:
$
F_g \propto \frac{m_1 m_2}{r_1 r_2}=\frac{m_1 m_2}{r \cdot r}=\frac{m_1 m_2}{r^2}
$
However, we want an equation, not a proportion.
If we multiply the right side of the equation, using the masses in kilograms and the distance in meters, we would get a much larger number than the actual force (in newtons). This means we have to include the conversion factor, which is called the “universal gravitational constant”. This constant turns out to be $6.67 \times 10^{-11} \frac{\mathrm{N} \cdot \mathrm{m}^2}{\mathrm{~kg}^2}$. (The units are because they cancel the $\mathrm{m}^2$ and $\mathrm{kg}^2$ from the formula and give newtons, which is the desired unit.) The symbol used for this constant is $G$. Thus our formula becomes:
$
F_g=\frac{G m_1 m_2}{r^2}=\frac{\left(6.67 \times 10^{-11}\right) m_1 m_2}{r^2}
$
This relationship is the universal gravitation equation. Sir Isaac Newton first published this equation in Philosophiæ Naturalis Principia Mathematica in 1687.
Relationship between $\boldsymbol{G}$ and $\boldsymbol{g}$
The strength of the gravitational field anyplace in the universe can be calculated from the universal gravitation equation.
If $m_1$ is the mass of the Earth (or whichever planet we happen to be standing on) and $m_2$ is the object that is being attracted, we can divide the universal gravitation equation by $m_2$, which gives us:
$
\frac{F_g}{m_2}=\frac{G m_1 \not F_2}{r^2 D p_2}=\frac{G m_1}{r^2}
$
Recall from the section on Gravitational Fields on page 254 that $\overrightarrow{\boldsymbol{F}}_g=m \overrightarrow{\boldsymbol{g}}$. For our object, which we’re calling $m_2$, this means that $\overrightarrow{\boldsymbol{g}}=\frac{\overrightarrow{\boldsymbol{F}}_g}{m_2}$.
Therefore, $g=\frac{G m_1}{r^2}$ where $m_1$ is the mass of the planet in question.
If we wanted to calculate the value of $g$ on Earth, In this expression, $m_1$ would be the mass of the Earth $\left(5.97 \times 10^{24} \mathrm{~kg}\right.$ ) and $r$ would be the radius of the Earth
$\left(6.38 \times 10^6 \mathrm{~m}\right)$. Substituting these numbers into the equation gives:
$
g=\frac{G m_1}{r^2}=\frac{\left(6.67 \times 10^{-11}\right)\left(5.97 \times 10^{24}\right)}{\left(6.38 \times 10^6\right)^2}=9.81 \mathrm{~N}^*
$
${ }^*$ In most places in this book we round $g$ to $10 \frac{\mathrm{N}}{\mathrm{kg}}$ to simplify the math. However, we have 3 significant figures for $G$, which means that if we want to compare results, we need to also use 3 significant figures for $g$.
Sample Problems:
Q: Find the force of gravitational attraction between the Earth and a person with a mass of $75 \mathrm{~kg}$. The mass of the Earth is $5.97 \times 10^{24} \mathrm{~kg}$, and its radius is $6.37 \times 10^6 \mathrm{~m}$
Answer/Explanation
$\mathrm{A}: \quad F_g=\frac{G m_1 m_2}{r^2}$
$
\begin{aligned}
& F_g=\frac{\left(6.67 \times 10^{-11}\right)\left(5.97 \times 10^{24}\right)(75)}{\left(6.38 \times 10^6\right)^2} \\
& F_g=736 \mathrm{~N}
\end{aligned}
$
This is the same number that we would get using $F_g=m g$, with $g=9.81 \frac{\mathrm{N}}{\mathrm{kg}}$.
If we use the approximation of $g=10 \frac{\mathrm{N}}{\mathrm{kg}}$ (which is about $2 \%$ too high), we get $F_g=750 \mathrm{~N}$, which is about $2 \%$ too high.
Question
Q: Find the acceleration due to gravity on the moon.
Answer/Explanation
$
\begin{aligned}
\text { A: } \quad g_{\text {moon }} & =\frac{G m_{\text {moon }}}{r_{\text {moon }}^2} \\
g_{\text {moon }} & =\frac{\left(6.67 \times 10^{-11}\right)\left(7.35 \times 10^{22}\right)}{\left(1.74 \times 10^6\right)^2}=1.62 \frac{\mathrm{N}}{\mathrm{kg}}
\end{aligned}
$