Projectile Motion
Notes:projectile: an object that is propelled (thrown, shot, etc.) horizontally and also falls due to gravity.
Because perpendicular vectors do not affect each other, the vertical and horizontal motion of the projectile are independent and can be considered separately, using a separate set of equations for each.
Assuming we can neglect friction and air resistance (which is usually the case in firstyear physics problems), we make the following important assumptions:
Horizontal Motion
The horizontal motion of a projectile is not affected by anything except for air resistance. If air resistance is negligible, we can assume that there is no horizontal acceleration, and therefore the horizontal velocity of the projectile, $\vec{v}_x$, is constant. This means the horizontal motion of a projectile can be described by the equation:
$$
\overrightarrow{\boldsymbol{d}}_x=\overrightarrow{\boldsymbol{v}}_x t
$$
The projectile is always moving in the same horizontal direction, so we make this the positive (horizontal, or ” $x$ “) direction for the vector quantities of velocity and displacement.
Vertical Motion
Gravity affects projectiles the same way regardless of whether or not the projectile is also moving horizontally. All projectiles therefore have a constant downward acceleration of $g=10 \frac{\mathrm{m}}{\mathrm{s}^2}$ (in the vertical or ” $y$ ” direction), due to gravity.
Therefore, the vertical motion of the particle can be described by the equations:
$
\begin{aligned}
& \overrightarrow{\boldsymbol{v}}_y-\overrightarrow{\boldsymbol{v}}_{o, y}=\overrightarrow{\boldsymbol{g}} t \\
& \overrightarrow{\boldsymbol{d}}_y=\overrightarrow{\boldsymbol{v}}_{o, y} t+\frac{1}{2} g t^2 \\
& \overrightarrow{\boldsymbol{v}}_y^2-\overrightarrow{\boldsymbol{v}}_{o, y}^2=2 \overrightarrow{\boldsymbol{g}} \overrightarrow{\boldsymbol{d}}
\end{aligned}
$
(Notice that we have two subscripts for initial velocity, because it is both the initial velocity $v_0$ and also the vertical velocity $v_y$.)
If the projectile is always moving downwards (i.e., it is launched horizontally and it falls), we make down the positive vertical direction and all vector quantities (velocity, displacement and acceleration) in the $y$-direction are positive.
If the projectile is launched upwards, reaches a maximum height, and then falls, the velocity and displacement are sometimes upwards and sometimes downwards. In this case, we need to choose a direction (usually upwards) to be positive. This makes $\overrightarrow{\boldsymbol{v}}_{o, y}$ positive, and makes $\overrightarrow{\boldsymbol{v}}_y$ and $\overrightarrow{\boldsymbol{g}}$ both negative. (In fact, $\overrightarrow{\boldsymbol{g}}=-10 \frac{\mathrm{m}}{\mathrm{s}^2}$.)
Time
The time that the projectile spends falling must be the same as the time that the projectile spends moving horizontally. This means time $(t)$ is the same in both equations, which means time is the variable that links the vertical problem to the horizontal problem.
The consequences of these assumptions are:
• The time that the object takes to fall is determined by its movement only in the vertical direction.
• The horizontal distance that the object travels is determined by the time (from the vertical equation) and its velocity in the horizontal direction.
Therefore, the general strategy for most projectile problems is:
1. Solve the vertical problem first, to get the time.
2. Use the time from the vertical problem to solve the horizontal problem.
Sample problem:
Q: A ball is thrown horizontally at a velocity of $5 \frac{\mathrm{m}}{\mathrm{s}}$ from a height of $1.5 \mathrm{~m}$. How far does the ball travel (horizontally)?
Answer/Explanation
A: We’re looking for the horizontal distance, $d_x$. We know the vertical distance, $d_y=1.5 \mathrm{~m}$, and we know that $v_{o, y}=0$ (there is no initial vertical velocity because the ball is thrown horizontally), and we know that $a_y=g=10 \frac{\mathrm{m}}{\mathrm{s}^2}$.
We need to separate the problem into the horizontal and vertical components.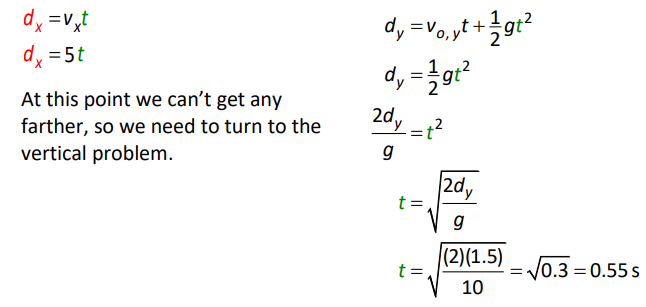
Now that we know the time, we can substitute it back into the horizontal equation, giving:
$
d_x=(5)(0.55)=2.74 \mathrm{~m}
$
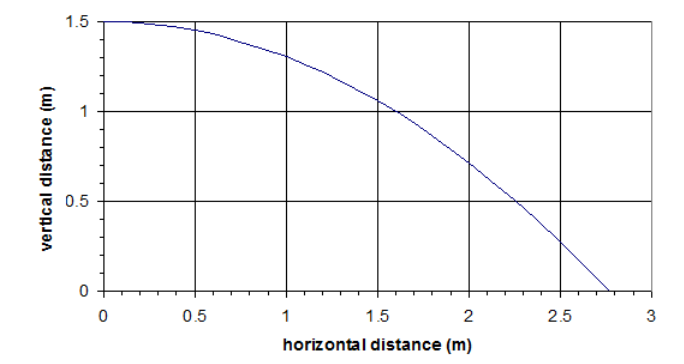
A graph of the vertical vs. horizontal motion of the ball looks like this:
Projectiles Launched at an Angle
If the object is thrown/launched at an angle, you will need to use trigonometry to separate the velocity vector into its horizontal $(x)$ and vertical $(y)$ components:
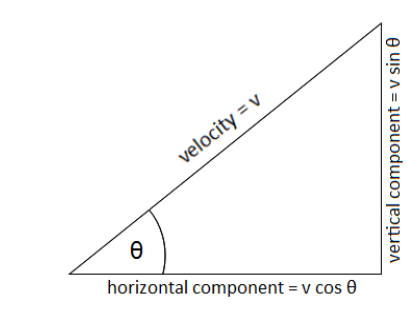
Thus:
– horizontal velocity $=v_x=v \cos \theta$
– $\quad$ initial vertical velocity $=v_{o, y}=v \sin \theta$
Note that the vertical component of the velocity, $v_y$, is constantly changing because of acceleration due to gravity:
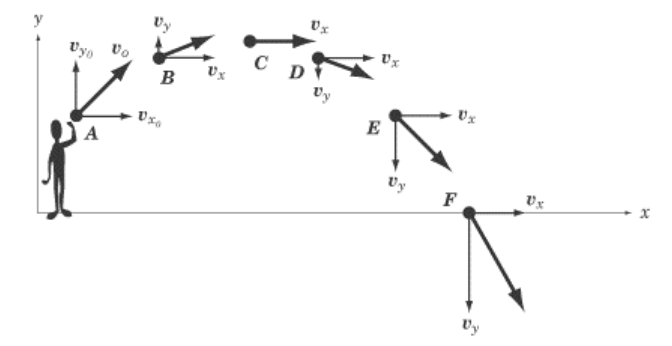
A fact worth remembering is that an angle of 45° gives the greatest horizontal displacement.
What AP® Projectile Problems Look Like
$\mathrm{AP}^{\oplus}$ motion and acceleration problems almost always involve graphs or projectiles. Here is an example that involves both:

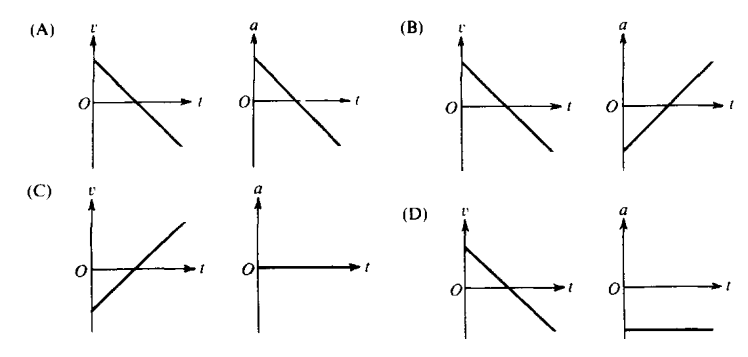
A projectile is fired with initial velocity $v_0$ at an angle $\theta_0$ with the horizontal and follows the trajectory shown above. Which of the following pairs of graphs best represents the vertical components of the velocity and acceleration, $v$ and $a$, respectively, of the projectile as functions of time t?
A: Because the object is a projectile:
•It can move both vertically and horizontally.
• It has a nonzero initial horizontal velocity. However, because the problem is asking about the vertical components, we can ignore the horizontal velocity.
•It has a constant acceleration of $-g$ (i.e., $g$ in the downward direction) due to gravity.
For each pair of graphs, the first graph is velocity vs. time. The slope, $\frac{\Delta v}{\Delta t}$, is acceleration. Because acceleration is constant, the graph has to have a constant. if we choose up to be the positive direction (which is the most common convention), correct answers would be (A), (B), and (D). If we choose down to be positive, only $(C)$ would be correct.
The second graph is acceleration vs. time. We know that acceleration is constant, which eliminates choices (A) and (B). We also know that acceleration is not zero, which eliminates choice (C). This leaves choice $(D)$ as the only possible remaining answer. Choice (D) correctly shows a constant negative acceleration, because the slope of the first graph is negative, and the $y$-value of the second graph is also negative.
A ball of mass $m$, initially at rest, is kicked directly toward a fence from a point that is a distance $d$ away, as shown above. The velocity of the ball as it leaves the kicker’s foot is $v_o$ at an angle of $\theta$ above the horizontal. The ball just clears the top of the fence, which has a height of $h$. The ball hits nothing while in flight and air resistance is negligible.
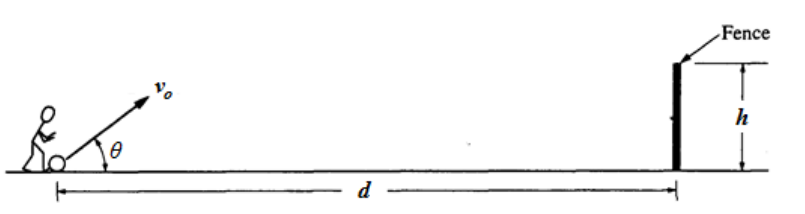
a. Determine the time, $t$, that it takes for the ball to reach the plane of the fence, in terms of $v_0, \theta, d$, and appropriate physical constants.
The horizontal component of the velocity is $v_h=v_o \cos \theta=\frac{d}{t}$.
Solving this expression for $t$ gives $t=\frac{d}{v_o \cos \theta}$.
Angular Motion, Speed and Velocity
Notes:
If an object is rotating (traveling in a circle), then its position at any given time can be described using polar coördinates by its distance from the center of the circle $(r)$ and its angle $(\theta)$ relative to some reference angle (which we will call $\theta=0$ ).
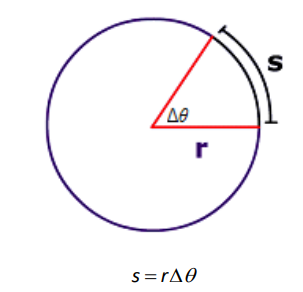
arc length $(s)$ : the length of an arc; the distance traveled around part of a circle.
angular velocity $(\omega)$ : the rotational velocity of an object as it travels around a circle, i.e., its change in angle per unit of time. (For purposes of comparison, the definition of angular velocity is presented along with its linear counterpart.)
$$
\begin{aligned}
& \overrightarrow{\boldsymbol{v}}=\frac{\overrightarrow{\boldsymbol{d}}}{t}=\frac{\Delta \overrightarrow{\boldsymbol{x}}}{\Delta t}=\frac{\overrightarrow{\boldsymbol{x}}-\overrightarrow{\boldsymbol{x}}_o}{t} \quad \overrightarrow{\boldsymbol{\omega}}=\frac{\Delta \overrightarrow{\boldsymbol{\theta}}}{\Delta t}=\frac{\overrightarrow{\boldsymbol{\theta}}-\overrightarrow{\boldsymbol{\theta}}_o}{t} \\
& \text { linear angular } \\
&
\end{aligned}
$$
In general, physicists use Greek letters for angular variables. The variable for angular velocity is the lower case Greek letter omega $(\omega)$. Be careful to distinguish in your writing between the Greek letter ” $\omega$ ” and the Roman letter “w”.
tangential velocity: the linear velocity of a point on a rigid, rotating body. The term tangential velocity is used because the instantaneous direction of the velocity is tangential to the direction of rotation.
To find the tangential velocity of a point on a rotating (rigid) body, the point travels an arc length of $s$ in time $t$. If angle $\theta$ is in radians, then $s=r \Delta \theta$. This means:
$$
\overrightarrow{\boldsymbol{v}}_{T, \text { ave. }}=\frac{\Delta \overrightarrow{\boldsymbol{s}}}{\Delta t}=\frac{r \Delta \overrightarrow{\boldsymbol{\theta}}}{\Delta t}=r \overrightarrow{\boldsymbol{\omega}}_{\text {ave. }} \quad \text { and therefore } \quad \overrightarrow{\mathbf{v}}_T=r \overrightarrow{\boldsymbol{\omega}}
$$
Sample Problems:
Q: What is the angular velocity $\left(\frac{\text { rad }}{s}\right)$ in of a car engine that is spinning at $2400 \mathrm{rpm}$ ?
Answer/Explanation
A: $2400 \mathrm{rpm}$ means 2400 revolutions per minute.
$
\left(\frac{2400 \mathrm{rev}}{1 \mathrm{nain}}\right)\left(\frac{1 \mathrm{~min}}{60 \mathrm{~s}}\right)\left(\frac{2 \pi \mathrm{rad}}{1 \mathrm{rev}}\right)=\frac{4800 \pi}{60}=80 \pi \frac{\mathrm{rad}}{\mathrm{s}}=251 \frac{\mathrm{rad}}{\mathrm{s}}
$
Q: Find the total distance traveled in 10 s by a penny sitting on a spinning disc with a radius of $0.25 \mathrm{~m}$ that is rotating at a rate of 1 revolution per $2 \mathrm{~s}$.
Answer/Explanation
A: We are looking for the distance around the circle, which is the arc length. (This means we need to work in radians.)
We know that:
$
\overrightarrow{\boldsymbol{s}}=r \Delta \overrightarrow{\boldsymbol{\theta}}
$
and we know:$
\Delta \overrightarrow{\boldsymbol{\theta}}=\overrightarrow{\boldsymbol{\omega}} t
$
Substituting the second equation into the first gives:
$
\overrightarrow{\boldsymbol{s}}=r \Delta \overrightarrow{\boldsymbol{\theta}}=r \overrightarrow{\boldsymbol{\omega}} t
$
We need to convert $\vec{\omega}$ to $\frac{\text { rad }}{\mathrm{s}}$ :
Extension
Just as jerk is the rate of change of linear acceleration, angular jerk is the rate of change of angular acceleration. $\vec{\zeta}=\frac{\Delta \overrightarrow{\boldsymbol{\alpha}}}{\Delta t}$. ( $\zeta$ is the Greek letter “zeta”. Many college professors cannot draw it correctly and just call it “squiggle”.) Angular jerk has not been seen on $A^{\oplus}{ }^{\oplus}$ Physics exams.
Angular Acceleration
Notes:
If a rotating object starts rotating faster or slower, this means its rotational velocity is changing.
angular acceleration $(\alpha)$ : the change in angular velocity with respect to time. (Again, the definition is presented with the linear equation for comparison.)
$
\begin{array}{cc}
\overrightarrow{\boldsymbol{a}}=\frac{\Delta \overrightarrow{\boldsymbol{v}}}{\Delta t}=\frac{\overrightarrow{\boldsymbol{v}}-\overrightarrow{\boldsymbol{v}}_o}{t} & \overrightarrow{\boldsymbol{\alpha}}=\frac{\Delta \overrightarrow{\boldsymbol{\omega}}}{\Delta t}=\frac{\overrightarrow{\boldsymbol{\omega}}-\overrightarrow{\boldsymbol{\omega}}_o}{t} \\
\text { linear } & \text { angular }
\end{array}
$
As before, be careful to distinguish between the lower case Greek letter ” $\alpha$ ” and the lower case Roman letter ” $a$ “.
As with linear acceleration, if the object has angular velocity and then accelerates, the position equation looks like this:
$
\begin{aligned}
& \overrightarrow{\boldsymbol{x}}-\overrightarrow{\boldsymbol{x}}_o=\overrightarrow{\boldsymbol{d}}=\overrightarrow{\boldsymbol{v}}_o t+\frac{1}{2} \overrightarrow{\boldsymbol{a}} t^2 \quad \overrightarrow{\boldsymbol{\theta}}-\overrightarrow{\boldsymbol{\theta}}_o=\Delta \overrightarrow{\boldsymbol{\theta}}=\overrightarrow{\boldsymbol{\omega}}_o t+\frac{1}{2} \overrightarrow{\boldsymbol{\alpha}} t^2 \\
& \text { linear angular } \\
&
\end{aligned}
$
tangential acceleration: the linear acceleration of a point on a rigid, rotating body. The term tangential acceleration is used because the instantaneous direction of the acceleration is tangential to the direction of rotation.
The tangential acceleration of a point on a rigid, rotating body is:
$
\overrightarrow{\boldsymbol{a}}_T=r \overrightarrow{\boldsymbol{\alpha}}
$
Sample Problem:
Q: A bicyclist is riding at an initial (linear) velocity of $7.5 \frac{\mathrm{m}}{\mathrm{s}}$, and accelerates to a velocity of $10.0 \frac{\mathrm{m}}{\mathrm{s}}$ over a duration of $5.0 \mathrm{~s}$. If the wheels on the bicycle have a radius of $0.343 \mathrm{~m}$, what is the angular acceleration of the bicycle wheels?
Answer/Explanation
A: First we need to find the initial and final angular velocities of the bike wheel. We can do this from the tangential velocity, which equals the velocity of the bicycle.
$
\begin{aligned}
\overrightarrow{\boldsymbol{v}}_{o, T} & =r \vec{\omega}_o & \overrightarrow{\boldsymbol{v}}_T & =r \overrightarrow{\boldsymbol{\omega}} \\
\frac{\overrightarrow{\boldsymbol{v}}_{o, T}}{r} & =\vec{\omega}_o & \frac{\overrightarrow{\boldsymbol{v}}_T}{r} & =\overrightarrow{\boldsymbol{\omega}} \\
\frac{7.5}{0.343} & =\vec{\omega}_o=21.87 \frac{\mathrm{rad}}{\mathrm{s}} & \frac{10.0}{0.343} & =\overrightarrow{\boldsymbol{\omega}}=29.15 \frac{\mathrm{rad}}{\mathrm{s}}
\end{aligned}
$
Then we can use the equation: $
\begin{aligned}
\overrightarrow{\boldsymbol{\omega}}-\overrightarrow{\boldsymbol{\omega}}_o & =\vec{\alpha} t \\
\frac{\overrightarrow{\boldsymbol{\omega}}-\overrightarrow{\boldsymbol{\omega}}_o}{t} & =\vec{\alpha} \\
\frac{29.15-21.87}{5.0} & =\vec{\alpha}=1.46 \frac{\mathrm{rad}}{\mathrm{s}^2}
\end{aligned}
$
An alternative method is to solve the equation by finding the linear acceleration first:
$
\begin{aligned}
\overrightarrow{\boldsymbol{v}}-\overrightarrow{\boldsymbol{v}}_o & =\vec{a} t \\
\frac{\overrightarrow{\boldsymbol{v}}-\overrightarrow{\boldsymbol{v}}_o}{t} & =\vec{a} \\
\frac{10.0-7.5}{5} & =\vec{a}=0.5 \frac{\mathrm{m}}{\mathrm{s}^2}
\end{aligned}
$
Then we can use the relationship between tangential acceleration and angular acceleration:
$
\begin{aligned}
\overrightarrow{\boldsymbol{a}}_\tau & =r \vec{\alpha} \\
\frac{\overrightarrow{\boldsymbol{a}}_\tau}{r} & =\vec{\alpha} \\
\frac{0.5}{0.343} & =\vec{\alpha}=1.46 \frac{\mathrm{rad}}{\mathrm{s}^2}
\end{aligned}
$
Centripetal Motion
Notes:
If an object is moving at a constant speed around a circle, its speed is constant, its direction keeps changing as it goes around. Because velocity is a vector (speed and direction), this means its velocity is constantly changing. (To be precise, the magnitude is staying the same, but the direction is changing.)
Because a change in velocity over time is acceleration, this means the object is constantly accelerating. This continuous change in velocity is toward the center of the circle, which means there is continuous acceleration toward the center of the circle.
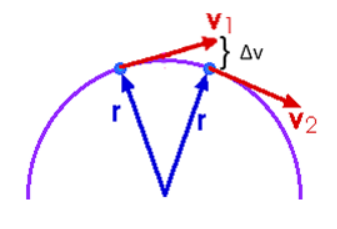
centripetal acceleration $\left(a_c\right)$ : the constant acceleration of an object toward the center of rotation that keeps it rotating around the center at a fixed distance.
The equation ${ }^*$ for centripetal acceleration $\left(a_c\right)$ is:
$
a_c=\frac{v^2}{r}=\frac{(r \omega)^2}{r}=r \omega^2
$
(The derivation of this equation requires calculus, so it will not be presented here.)
Sample Problem:
Q: A weight is swung from the end of a string that is $0.65 \mathrm{~m}$ long at a rate of rotation of 10 revolutions in $6.5 \mathrm{~s}$. What is the centripetal acceleration of the weight? How many “g’s” is that? (I.e., how many times the acceleration due to gravity is the centripetal acceleration?)
Answer/Explanation
A: There are two ways to solve this problem.
Without using angular velocity:
In each revolution, the object travels a distance of $2 \pi r$ :
$
s_{\text {rev }}=2 \pi r=(2)(3.14)(0.65)=4.08 \mathrm{~m}
$
The total distance for 10 revolutions is therefore: $s=(4.08)(10)=40.8 \mathrm{~m}$
The velocity is the distance divided by the time: $v=\frac{d}{t}=\frac{40.8}{6.5}=6.28 \frac{\mathrm{m}}{\mathrm{s}}$
Finally, $a_c=\frac{v^2}{r}=\frac{(6.28)^2}{0.65}=60.7 \frac{\mathrm{m}}{\mathrm{s}^2}$
This is $\frac{60.7}{10}=6.07$ times the acceleration due to gravity.
Using angular velocity:
The angular velocity is:
$
\left(\frac{10 \mathrm{rev}}{6.5 \mathrm{~s}}\right)\left(\frac{2 \pi \mathrm{rad}}{1 \mathrm{rev}}\right)=\frac{20 \pi}{6.5}=9.67 \frac{\mathrm{rad}}{\mathrm{s}}
$
The centripetal acceleration is therefore:
$
\begin{aligned}
& a_c=r \omega^2 \\
& a_c=(0.65)(9.67)^2=(0.65)(93.44)=60.7 \frac{\mathrm{m}}{\mathrm{s}^2}
\end{aligned}
$
This is $\frac{60.7}{10}=6.07$ times the acceleration due to gravity.
${ }^*$ Centripetal motion relates to angular motion (which is studied in $A P^{\oplus}$ Physics but not in the CP1 or honors courses). Equations or portions of equations with angular velocity $(\omega)$ and angular acceleration $(\alpha)$ apply only to the $A P^{\oplus}$ course.
Solving Linear & Rotational Motion Problems
Notes:
The following is a summary of the variables used for motion problems. Note the correspondence between the linear and angular quantities.

Notice that each of the linear variables has an angular counterpart.
Note that “radian” is not a unit. A radian is a ratio that describes an angle as the ratio of the arc length to the radius. This ratio is dimensionless (has no unit), because the units cancel. This means that an angle described in radians has no unit, and therefore never needs to be converted from one unit to another. However, we often write “rad” after an angle measured in radians to remind ourselves that the quantity describes an angle.
We have learned the following equations for solving motion problems. Again, note the correspondence between the linear and angular equations.

Note that vector quantities can be positive or negative, depending on direction.
Note that $\overrightarrow{\boldsymbol{r}}, \overrightarrow{\boldsymbol{\omega}}$ and $\overrightarrow{\boldsymbol{\alpha}}$ are vector quantities. However, the equations that relate linear and angular motion and the centripetal acceleration equations apply to magnitudes only, because of the differences in coordinate systems and changing frames of reference.
Selecting the Right Equation
(This is the same as the list from page 184 , with the addition of angular velocity.) When you are faced with a problem, choose an equation based on the following criteria:
•The equation must contain the variable you are looking for.
•All other quantities in the equation must be either given in the problem or assumed from the description of the problem.

This means you can choose the appropriate equation by making a list of what you are looking for and what you know. The equation in which you know everything except what you are looking for is the one to use.