Introduction
In this chapter, you will study how things move and how the relevant quantities are related.
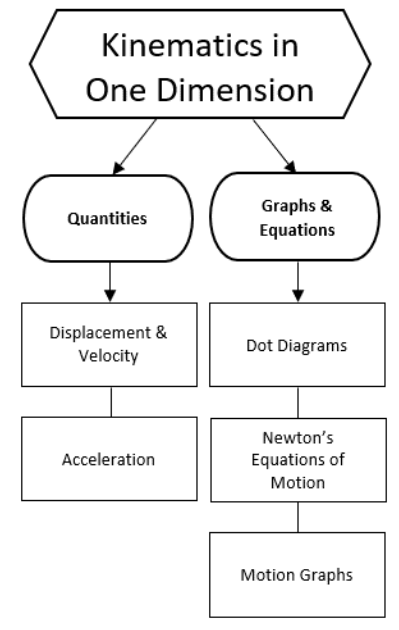
- Linear Motion, Speed & Velocity and Acceleration deal with understanding and calculating the velocity (change in position) and acceleration (change in velocity) of an object, and with representing and interpreting graphs involving these quantities.
- Dot Diagrams deals with a representation of motion using a series of dots that show the location of an object at equal time intervals.
- Newton’s Equations of Motion deals with solving motion problems algebraically, using equations.
- Motion Graphs deals with creating and interpreting graphs of position vs. time and velocity vs. time. Some of the challenging tasks include identifying quantities from their units, choosing the equation that relates the quantities of interest, and keeping track of positive and negative directions when working with vector quantities.
Linear Motion, Speed & Velocity
Notes: coördinate system: a framework for describing an object’s position (location), based on its distance (in one or more directions) from a specifically-defined point (the oriqin). (You should remember these terms from math.)
direction: which way an object is oriented or moving within its coördinate system. Note that direction can be positive or negative.
position $(\overrightarrow{\boldsymbol{x}})$ : [vector*] the location of an object relative to the origin (zero point) of its coördinate system. We will consider position to be a zero-dimensional vector, which means position can be positive or negative with respect to the chosen coördinate system.
distance $(d)$ : [scalar] the length of the path that an object took when it moved. Distance does not depend on direction and is always positive or zero.
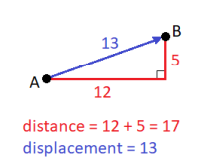
displacement $(\overrightarrow{\boldsymbol{d}}$ or $\Delta \overrightarrow{\boldsymbol{x}})$ : [vector] how far an object’s current position is from its starting position (“initial position”).
For example, suppose an object travelled a distance of 12 units to the east, and then 5 units to the north. The object has travelled a total distance of 17 units, However, by the Pythagorean theorem, the object’s displacement is 13 units from where it started.
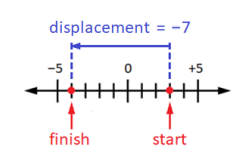
Displacement can be positive or negative (or zero), depending on the chosen coördinate system. For example, the object at the right’s displacement is -7 units (7 units in the negative direction) from where it started.
” Position is a zero-dimensional vector. An object’s position is a location that, like other vector quantities, can be positive or negative and is dependent on the coördinate system chosen.
rate: the change in a quantity over a specific period of time.
motion: when an object’s position is changing over time.
speed: [scalar] the rate at which an object is moving at an instant in time. Speed does not depend on direction, and is always positive or zero.
$
\text { average speed }=\frac{\text { distance }}{\text { time }}
$
velocity: ( $\overrightarrow{\boldsymbol{v}})$ [vector] the rate of change of an object’s position (its displacement) over a given period of time. Because velocity is a vector, it has a direction as well as a magnitude. Velocity can be positive, negative, or zero.
$
\text { average velocity }=\frac{\text { displacement }}{\text { time }} \quad \overrightarrow{\boldsymbol{v}}_{\text {ave. }}=\frac{\overrightarrow{\boldsymbol{d}}}{t}=\frac{\Delta \boldsymbol{x}}{t}
$
In the MKS system, speed and velocity are measured in meters per second.
$
1 \frac{\mathrm{m}}{\mathrm{s}} \approx 2.24 \frac{\mathrm{mi}}{\mathrm{hr} .}
$
uniform motion: motion at a constant velocity (i.e., with constant speed and direction)
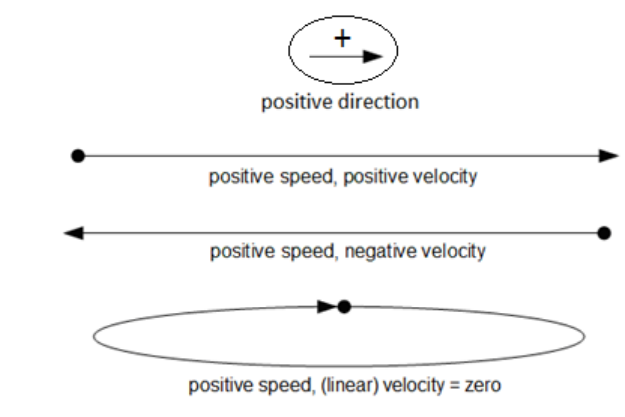
An object that is moving has a positive speed, but its velocity may be positive, negative, or zero, depending on the relationship between its initial and final position.
Acceleration will be covered in the next section.
By convention, physicists use the variable $\overrightarrow{\boldsymbol{g}}$ to mean acceleration due to gravity of an object in free fall, and $\overrightarrow{\boldsymbol{a}}$ to mean acceleration under any other conditions.
The average velocity of an object is its displacement (change in position) divided by the elapsed time:
The acceleration of an object is its change in velocity divided by the elapsed time:
$
\overrightarrow{\boldsymbol{a}}=\frac{\Delta \overrightarrow{\boldsymbol{v}}}{t}
$
Note that by convention, physicists use the variable $\overrightarrow{\boldsymbol{g}}$ when acceleration is due to gravity acting on an object in free fall, and $\overrightarrow{\boldsymbol{a}}$ to mean acceleration caused by something other than gravity.
Signs of Vector Quantities
The sign of a vector (positive or negative) is used to indicate its direction.
• Displacement is positive if the change in position of object in question is toward the positive direction, and negative if the change in position is toward the negative direction.
• Velocity is positive if the object is moving in the positive direction, and negative if the object is moving in the negative direction.
• Acceleration is positive if the change in velocity is positive (i.e., if the velocity is becoming more positive or less negative). Acceleration is negative if the change in velocity is negative (i.e., if the velocity is becoming less positive or more negative).
Linear Acceleration
Notes: acceleration $(\overrightarrow{\boldsymbol{a}})$ : [vector] a change in velocity; the rate of change of velocity.
$
\overrightarrow{\boldsymbol{a}}=\frac{\Delta \overrightarrow{\boldsymbol{v}}}{t}=\frac{\overrightarrow{\boldsymbol{v}}-\overrightarrow{\boldsymbol{v}}_o}{t}
$
The MKS unit for acceleration is $\frac{\mathrm{m}}{\mathrm{s}^2}$. This is because $\Delta \overrightarrow{\vec{v}}$ has units $\frac{\mathrm{m}}{\mathrm{s}}$, which means $\overrightarrow{\boldsymbol{a}}=\frac{\Delta \overrightarrow{\boldsymbol{v}}}{t}$ has units $\frac{\mathrm{m} / \mathrm{s}}{\mathrm{s}}=\frac{\mathrm{m}}{\mathrm{s}} \cdot \frac{1}{\mathrm{~s}}=\frac{\mathrm{m}}{\mathrm{s}^2}$.
uniform acceleration: constant acceleration; a constant rate of change of velocity.
Because this is an algebra-based course, acceleration will be assumed to be uniform in all of the problems in this course that involve acceleration.
In the vernacular, we use the term “acceleration” to mean “speeding up,” and “deceleration” to mean “slowing down.”
In physics, acceleration is a vector quantity, which means it has a direction. If an object is moving in the positive direction (i.e., its velocity is positive), then positive acceleration would mean that the object is speeding up, and negative acceleration would mean that it is slowing down.
Note, however, that acceleration is any change in velocity, including a change in speed or a change in direction. There is a popular joke in which a physics student is taking a driving lesson. The instructor says, “Apply the accelerator.” The physics student replies, “Which one? I’ve got three!”

Calculating Acceleration
Suppose that instead of a speedometer, your car has a velocity meter, which displays a positive velocity when the car is going in the positive direction (forward) and a negative velocity when it is going in the negative direction (backward).
The following velocity meters show a car that starts out with a velocity of $+15 \frac{\mathrm{m}}{\mathrm{s}}$ and accelerates to $+40 \frac{\mathrm{m}}{\mathrm{s}}$. Suppose this acceleration happened over a time interval of $10 \mathrm{~s}$.
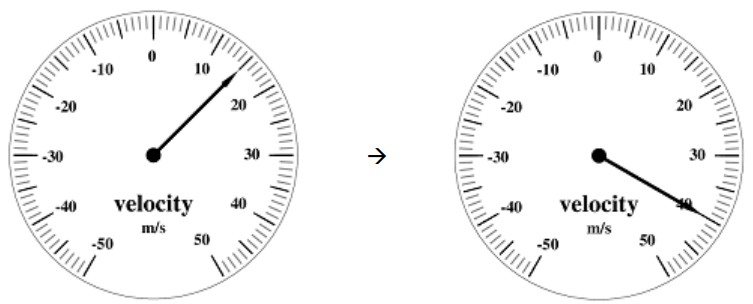
The car’s speed is faster at the end $\left(40 \frac{\mathrm{m}}{\mathrm{s}}\right.$ vs. $\left.15 \frac{\mathrm{m}}{\mathrm{s}}\right)$, and it is traveling in the positive direction the entire time. The change in velocity $(\Delta \overrightarrow{\boldsymbol{v}})$ is therefore
$
+40-(+15)=+25 \frac{\mathrm{m}}{\mathrm{s}}
$
The acceleration is therefore $\overrightarrow{\boldsymbol{a}}=\frac{\Delta \overrightarrow{\boldsymbol{v}}}{t}=\frac{+40-(+15)}{10}=\frac{+25}{10}=+2.5 \frac{\mathrm{m}}{\mathrm{s}^2}$
This is a simplification. A car can also change its velocity by changing direction-for example if the road curves. Displacement, and therefore velocity, is always in the direction from the starting point to the endpoint. An actual velocity meter would be more like a GPS that shows the direction and progress toward the destination on a map.
Free Fall (Acceleration Caused by Gravity)
The gravitational force is an attraction between objects that have mass.
free fall: when an object is freely accelerating toward the center of the Earth (or some other object with a very large mass) because of the effects of gravity, and the effects of other forces are negligible.
Objects in free fall on Earth accelerate downward at a rate of approximately $10 \frac{\mathrm{m}}{\mathrm{s}^2} \approx 32 \frac{\mathrm{ft}}{\mathrm{s}^2}$. (The actual number is approximately $9.807 \frac{\mathrm{m}}{\mathrm{s}^2}$ at sea level near the surface of the Earth. In this course we will usually round it to $10 \frac{\mathrm{m}}{\mathrm{s}^2}$ so the calculations don’t get in the way of understanding the physics.)
Note that an object going down a ramp is not in free fall even though gravity is the force that caused the object to accelerate. The object’s motion is constrained by the ramp and it is not free to fall straight down.
Acceleration Notes
• Whether acceleration is positive or negative is based on the trend of the velocity (changing toward positive vs. changing toward negative).
• An object can have a positive velocity and a negative acceleration at the same time, or vice versa.
• The sign (positive or negative) of an object’s velocity is the direction the object is moving. If the sign of the velocity changes (from positive to negative or negative to positive), the change indicates that the object’s motion has changed directions.
• An object can be accelerating even when it has a velocity of zero. For example, if you throw a ball upward, it goes up to its maximum height and then falls back to the ground. At the instant when the ball is at its maximum height, its velocity is zero, but gravity is still causing it to accelerate toward the Earth at a rate of $10 \frac{\mathrm{m}}{\mathrm{s}^2}$.
Extension
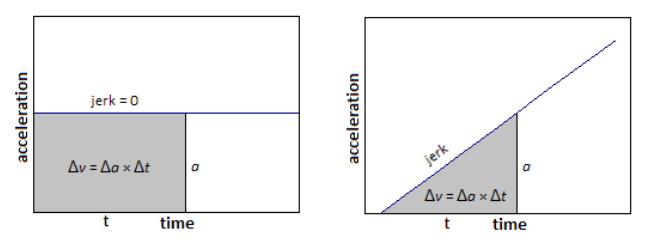
Just as a change in velocity is called acceleration, a change in acceleration with respect to time is called “jerk”: $\overrightarrow{\boldsymbol{j}}=\frac{\Delta \overrightarrow{\boldsymbol{a}}}{\Delta t}$.
Dot Diagrams
Notes:
The following is a famous picture called “Bob running”, taken by Harold “Doc” Edgerton, inventor of the strobe light.

To create this picture, Edgerton opened the shutter of a camera in a dark room. A strobe light flashed at regular intervals while a child named Bob ran past. Each flash captured an image of Bob as he was running past the camera.
The images show that Bob was running at a constant velocity, because in each image he had travelled approximately the same distance relative to the previous image.
If we simplify the picture and replace the images of Bob with stick figures, they might look like this:

If the time between flashes of the strobe light was exactly one second, we would know where the stick figure was at every second:
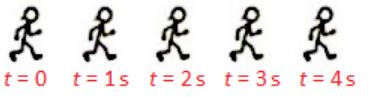
Notice that our stick figure travels the same amount of distance from one second to the next, because its velocity is constant. If we replaced the stick figures with dots, our diagram would look like this:

This is called a “dot diagram”. As with the stick figures, if the velocity is constant, the space between each dot and the next will also be constant.
Newton’s Equations of Motion
Notes:
As noted above, velocity is the displacement (change in position) with respect to time. (E.g., if your displacement is $10 \mathrm{~m}$ over a period of $2 \mathrm{~s}$, then your velocity is $\left.\frac{10}{2}=5 \frac{\mathrm{m}}{\mathrm{s}}.\right)$
Derivations of Equations
We can rearrange this formula to show that displacement is average velocity times time:
$
\overrightarrow{\boldsymbol{d}}=\left(\overrightarrow{\boldsymbol{v}}_{\text {ave. }}\right)(t)
$
Position is the object’s starting position plus its displacement:
$
x=x_o+\overrightarrow{\boldsymbol{d}}=x_o+\left(\overrightarrow{\boldsymbol{v}}_{\text {ave }}\right)(t)
$
where $x_0{ }^*$ means “position at time $=0$ “. This formula is often expressed as:
$
x-x_o=\overrightarrow{\boldsymbol{d}}=\left(\overrightarrow{\boldsymbol{v}}_{\text {ove }}\right)(t)
$
Because acceleration is a change in velocity over a period of time, the formula for acceleration is:
$
\overrightarrow{\boldsymbol{a}}_{\text {ave. }}=\frac{\overrightarrow{\boldsymbol{v}}-\overrightarrow{\boldsymbol{v}}_o}{t}=\frac{\Delta \overrightarrow{\boldsymbol{v}}}{t}=\frac{\Delta \overrightarrow{\boldsymbol{v}}}{\Delta t}
$
${ }^* x_0$ is pronounced ” $x$-zero” or ” $x$-naught”.
In an algebra-based physics course, we will limit ourselves to problems in which acceleration is constant.
We can rearrange this formula to show that the change in velocity is acceleration times time:
$
\Delta \overrightarrow{\boldsymbol{v}}=\overrightarrow{\boldsymbol{v}}-\overrightarrow{\boldsymbol{v}}_o=\overrightarrow{\boldsymbol{a}} t
$
Note that when an object’s velocity is changing, the initial velocity $\overrightarrow{\boldsymbol{v}}_0$, the final velocity, $\overrightarrow{\boldsymbol{v}}$, and the average velocity, $\vec{v}_{\text {ave. }}$ are different quantities with different values. (This is a common mistake that first-year physics students make.) Assuming acceleration is constant, the three different velocities are related by the following equation:
$
\overrightarrow{\boldsymbol{v}}_{\text {ove. }}=\frac{\overrightarrow{\boldsymbol{v}}_o+\overrightarrow{\boldsymbol{v}}}{2}=\frac{\overrightarrow{\boldsymbol{d}}}{t}
$
To show the relationship between $v$ and $v_{\text {ave. }}$, we can combine the formula for average velocity with the formula for acceleration in order to get a formula for the position of an object that is accelerating.
$
\begin{aligned}
& \boldsymbol{d}=\left(\boldsymbol{v}_{\text {ave. }}\right)(t) \\
& \boldsymbol{v}=\boldsymbol{a} t
\end{aligned}
$
However, the problem is that $\boldsymbol{v}$ in the formula $\boldsymbol{v}=\boldsymbol{a}$ is the velocity at the end, which is not the same as the average velocity $\boldsymbol{v}_{\text {ave. }}$.
If the velocity of an object is changing at a constant rate (i.e., the object is accelerating uniformly), the average velocity, $v_{\text {ove. }}$ is given by the formula:
$
\boldsymbol{v}_{\text {ave. }}=\frac{\boldsymbol{v}_o+\boldsymbol{v}}{2}
$
If the object starts at rest (not moving, which means $\boldsymbol{v}_o=0$ ) and it accelerates at a constant rate, the average velocity is therefore the average of the initial velocity and the final velocity:
$
\boldsymbol{v}_{\text {ave. }}=\frac{\boldsymbol{v}_o+\boldsymbol{v}}{2}=\frac{0+\boldsymbol{v}}{2}=\frac{\boldsymbol{v}}{2}=\frac{1}{2} \boldsymbol{v}
$
Combining all of these gives, for an object starting from rest:
$
\boldsymbol{d}=\boldsymbol{v}_{\text {ave. }} t=\frac{1}{2} \boldsymbol{v} t=\frac{1}{2}(\boldsymbol{a}) t=\frac{1}{2} \boldsymbol{a} t^2
$
If an object was moving before it started to accelerate, it had an initial velocity (or a velocity at time $=0$ ) that is not zero, which means we have to include the distance that the object would have traveled at a constant velocity of $v_0$ in the equation. Now, the formula becomes:
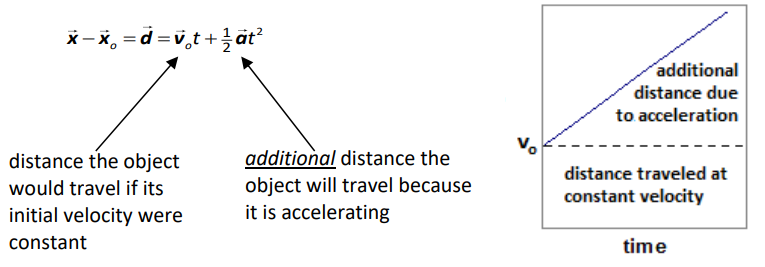
We can combine this equation with the equation $\overrightarrow{\boldsymbol{v}}-\overrightarrow{\boldsymbol{v}}_o=\overrightarrow{\boldsymbol{a}}$ and eliminate time, giving the following equation, which relates initial and final velocity and distance:
$
\overrightarrow{\boldsymbol{v}}^2-\overrightarrow{\boldsymbol{v}}_o^2=2 \overrightarrow{\boldsymbol{a}} \vec{d}
$
Free Fall (Acceleration Caused by Gravity)
The gravitational force (or “force of gravity”) is an attraction between objects that have mass.
free fall: when an object is freely accelerating toward the center of the Earth (or some other object with a very large mass) because of the effects of gravity, and the effects of other forces are negligible.
Objects in free fall on Earth accelerate downward at a rate of approximately $10 \frac{\mathrm{m}}{\mathrm{s}^2} \approx 32 \frac{\mathrm{ft}}{\mathrm{s}^2}$. (The actual number is approximately $9.807 \frac{\mathrm{m}}{\mathrm{s}^2}$ at sea level near the surface of the Earth. In this course we will usually round it to $10 \frac{\mathrm{m}}{\mathrm{s}^2}$ so the calculations don’t get in the way of understanding the physics.) When an object is in free fall, we usually replace the variable $\overrightarrow{\boldsymbol{a}}$ with the constant $\overrightarrow{\boldsymbol{g}}$.
Note that as with any other vector quantity, acceleration due to gravity can be represented by a positive or negative number, depending on which direction you choose to be positive. In many problems, it is common to choose “up” to be the positive direction, which would mean $\overrightarrow{\boldsymbol{a}}=\overrightarrow{\boldsymbol{g}}=-10 \frac{\mathrm{m}}{\mathrm{s}^2}$.
Note also that an object going down a ramp is not in free fall, even though gravity is the force that caused the object to accelerate. The object’s motion is constrained by the ramp and it is not free to fall straight down.
Selecting the Right Equation
When you are faced with a problem, choose an equation based on the following criteria:
• The equation must contain the variable you are looking for.
• All other quantities in the equation must be either given in the problem or assumed from the description of the problem.
- If an object starts from rest (not moving), that means $\vec{v}_0=0$.
- If an object comes to rest (stops), that means $\vec{v}=0$. (Remember that $\vec{v}$ is the velocity at the end.)
- If an object is moving at a constant velocity, then $\overrightarrow{\boldsymbol{v}}=$ constant $=\overrightarrow{\boldsymbol{v}}_o=\overrightarrow{\boldsymbol{v}}_{\text {ave }}$. and $\overrightarrow{\boldsymbol{a}}=0$.
- If the object is in free fall, that means $\overrightarrow{\boldsymbol{a}}=\overrightarrow{\boldsymbol{g}} \approx 10 \frac{\mathrm{m}}{\mathrm{s}^2}$. Look for words like drop, fall, throw, etc. (Does not apply to rotation problems.)
This means you can choose the appropriate equation by making a list of what you are looking for and what you know. The equation in which you know everything except what you are looking for is the one to use.
Representing Vectors with Positive and Negative Numbers
Remember that position $(\overrightarrow{\boldsymbol{x}})$, velocity $(\overrightarrow{\boldsymbol{v}})$, and acceleration $(\overrightarrow{\boldsymbol{a}})$ are all vectors, which means each of them can be positive or negative, depending on the direction.
• If an object is located is on the positive side of the origin (position zero), then its position, $\overrightarrow{\boldsymbol{x}}$, is positive. If the object is located on the negative side of the origin, its position is negative.
• If an object is moving in the positive direction, then its velocity, $\overrightarrow{\boldsymbol{v}}$, is positive. If the object is moving in the negative direction, then its velocity is negative.
• If an object’s velocity is “trending positive” (increasing in the positive direction or decreasing in the negative direction), then its acceleration, $\overrightarrow{\boldsymbol{a}}$, is positive. If the object’s velocity is “trending negative” (decreasing in the positive direction or increasing in the negative direction), then its acceleration is negative.
• An object can have positive velocity and negative acceleration at the same time (or vice versa).
• An object can have a velocity of zero (for an instant) but can still be accelerating.
Strategies for Linear Motion Problems Involving Gravity
Linear motion problems in physics often involve gravity.
1. If you have an object in free fall, the problem will probably give you either the distance it fell $\left(\overrightarrow{\boldsymbol{x}}-\overrightarrow{\boldsymbol{x}}_o=\overrightarrow{\boldsymbol{d}}\right.$ ), or the time it fell $(t)$. Use the position equation $\overrightarrow{\boldsymbol{x}}-\overrightarrow{\boldsymbol{x}}_0=\overrightarrow{\boldsymbol{d}}=\overrightarrow{\boldsymbol{v}}_0 t+\frac{1}{2} \overrightarrow{\boldsymbol{a}} t^2$ to calculate whichever one you don’t know. (If the object starts from rest, that means $\vec{v}_0=0$.)
2. If an object is thrown upwards, it will accelerate downwards. This means that if we choose the positive direction to be “up,” acceleration will be $-10 \frac{\mathrm{m}}{\mathrm{s}^2}$ (downwards, and therefore negative).
3. At an object’s maximum height, it stops moving for an instant $(\vec{v}=0)$.
4. If an object goes up and then falls down to the same height it started from:
a. The vertical displacement is zero.
b. The time that the object spends going upwards is the same as the time it spends going downwards. The time it takes to reach its maximum height is therefore half of the total time it takes to go up to its highest point and return to the ground.
c. The magnitude of the velocity at the end will be the same as at the beginning, but the direction will be opposite. $\left(\overrightarrow{\boldsymbol{v}}=-\overrightarrow{\boldsymbol{v}}_0\right)$
Sample problems:
Q: A car travels $1200 \mathrm{~m}$ in 60 seconds. What is its average velocity?
Answer/Explanation
A: $v_{\text {ave. }}=\frac{d}{t}=\frac{1200 \mathrm{~m}}{60 \mathrm{~s}}=20 \frac{\mathrm{m}}{\mathrm{s}}$
Q: A person walks $320 \mathrm{~m}$ at an average velocity of $1.25 \frac{\mathrm{m}}{\mathrm{s}}$. How long did it take?
Answer/Explanation
A: “How long” means what length of time.
$
\overrightarrow{\boldsymbol{v}}_{\text {ave. }}=\frac{\overrightarrow{\boldsymbol{d}}}{t} \quad\left(\overrightarrow{\boldsymbol{v}}_{\text {ave. }}\right) t=\overrightarrow{\boldsymbol{d}} \quad t=\frac{\overrightarrow{\boldsymbol{d}}}{\overrightarrow{\boldsymbol{v}}_{\text {ave. }}}=\frac{320}{1.25}=256 \mathrm{~s}
$
Notice that when solving for a variable in the denominator, it is safest to do it in two steps-first multiply both sides by the denominator and then divide to isolate the variable in a second step. Many students attempt to rearrange the variables in one step, often with little success.
Question
Q: If a cat jumps off a $1.8 \mathrm{~m}$ tall refrigerator, how long does it take to hit the ground?
Answer/Explanation
A: The cat is starting from rest $\left(v_{\circ}=0\right)$, and acceleration due to gravity is $a=g=10 \frac{\mathrm{m}}{\mathrm{s}^2}$. We need to find $t$.
Looking at the equations, the one that has what we need $(t)$ and only quantities we know is:
$
d=v_o t+\frac{1}{2} a t^2
$
$v_0=0$, so this reduces to:
$
d=\frac{1}{2} a t^2 \quad \frac{2 d}{a}=t^2 \quad t=\sqrt{\frac{2 d}{a}}=\sqrt{\frac{(2)(1.8)}{10}}=\sqrt{0.36}=0.6 \mathrm{~s}
$

Motion Graphs*
Notes:
Suppose you were to plot a graph of position vs. time for an object moving at a constant velocity.
Note that $\frac{\Delta x}{\Delta t}$ is the slope of a graph of position $(x) v s$. time $(t)$. Because $\frac{\Delta x}{\Delta t}=v$, this means that the slope of a graph of position vs. time is equal to the velocity.
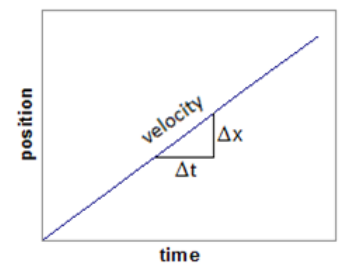
In fact, on any graph, the quantity you get when you divide the quantity on the $x$-axis by the quantity on the $y$-axis is, by definition, the slope. I.e., the slope is $\frac{\Delta y}{\Delta x}$, which means the physics quantity defined by $\frac{\Delta y \text {-axis }}{\Delta x \text {-axis }}$ will always be the slope.
Recall that velocity is a vector, which means it can be positive, negative, or zero.
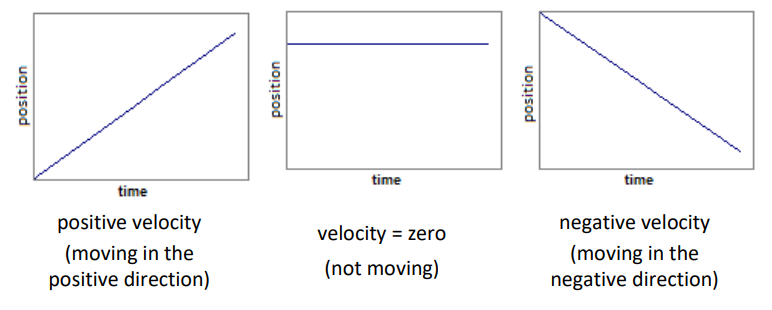
On the graph below, the velocity is $+4 \frac{\mathrm{m}}{\mathrm{s}}$ from $0 \mathrm{~s}$ to $2 \mathrm{~s}$, zero from $2 \mathrm{~s}$ to $4 \mathrm{~s}$, and $-2 \frac{m}{s}$ from $4 s$ to $8 s$.
Suppose now that you were to plot a graph of velocity vs. time.
$\frac{\Delta v}{\Delta t}$ is the slope of a graph of velocity $(v)$ vs. time
(t). Because $\frac{\Delta v}{\Delta t}=a$, this means that
acceleration is the slope of a graph of velocity vs. time.
Note the relationship between velocity-time graphs and position-time graphs.
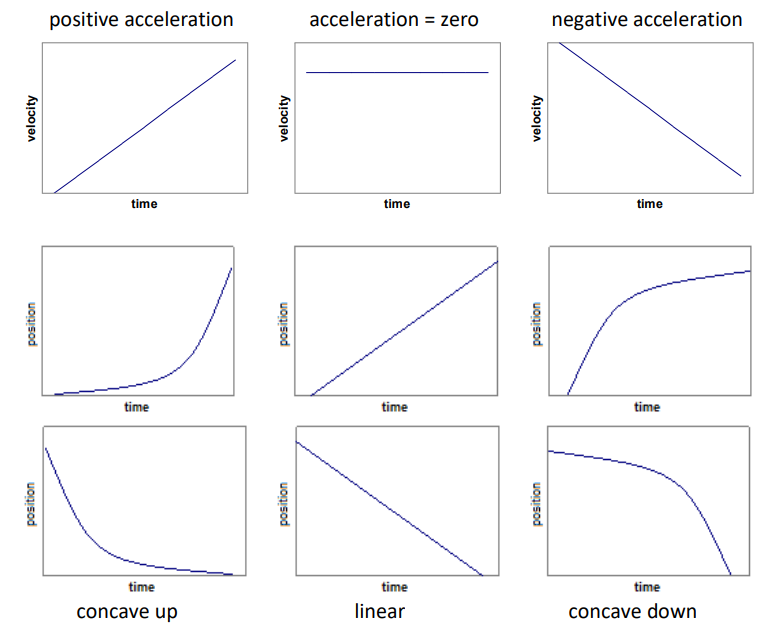
If the object’s velocity is positive:
•Positive acceleration would mean an the velocity is getting more positive, i.e., the object would be speeding up in the positive direction.
• Negative acceleration would mean an the velocity is getting less positive, i.e., the object would be slowing down in the positive direction. If the object’s velocity is negative:
•Positive acceleration would mean that the velocity is getting less negative, i.e., the object would be slowing down in the negative direction.
• Negative acceleration would mean that the velocity is getting more negative, i.e., the object would be speeding up in the negative direction.
Note also that $v_{\text {ave. }} t$ is the area under a graph (i.e., the area between the curve and the $x$-axis) of velocity $(v)$ vs. time $(t)$. Because $\left(v_{\text {ave. }}\right)(t)=d$, this means the area under a graph of velocity $v s$. time is the displacement $(\Delta x)$. Note that this works both for constant velocity (the graph on the left) and changing velocity (as shown in the graph on the right).
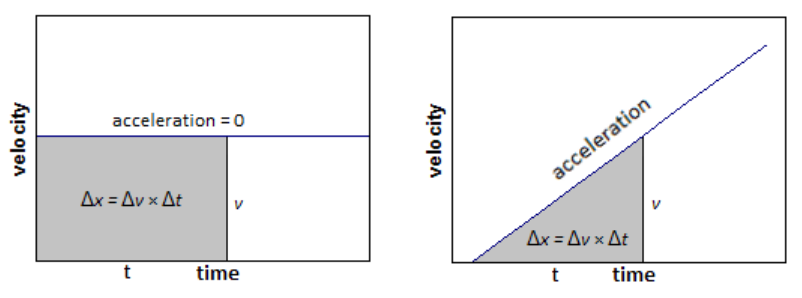
In fact, on any graph, the quantity you get when you multiply the quantities on the $x$ – and $y$-axes is, by definition, the area under the graph.
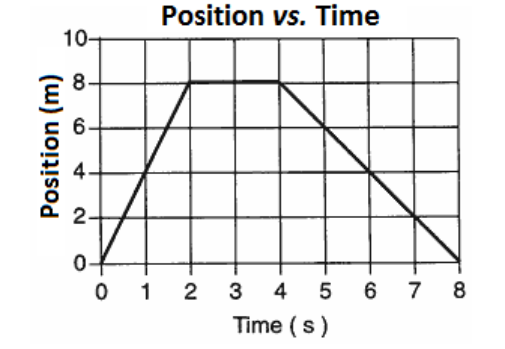
In the graphs below, between $0 \mathrm{~s}$ and $4 \mathrm{~s}$, the slope of the graph is 2.5 , which means the object is accelerating at a rate of $+2.5 \frac{\mathrm{m}}{\mathrm{s}^2}$.
Between $4 \mathrm{~s}$ and $6 \mathrm{~s}$ the slope is zero, which indicates that object is moving at a constant velocity (of $+10 \frac{\mathrm{m}}{\mathrm{s}}$ ) and the acceleration is zero.
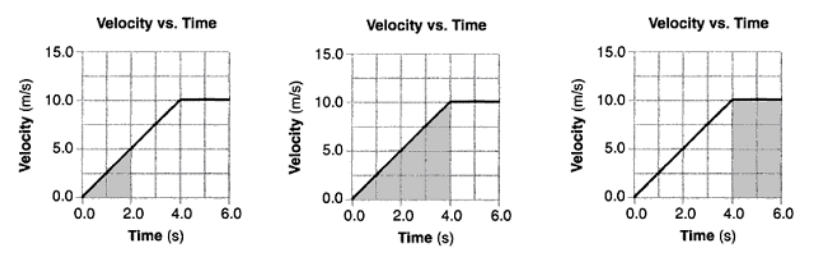
Between 0 and $2 \mathrm{~s}$
Between 0 and $4 \mathrm{~s}$
Between $4 \mathrm{~s}$ and $6 \mathrm{~s}$
$
\begin{array}{ccc}
a=2.5 \frac{\mathrm{m}}{\mathrm{s}^2} & a=2.5 \frac{\mathrm{m}}{\mathrm{s}^2} & a=0 \\
\text { area }=\frac{1}{2} b h=\frac{1}{2}(2)(5)=5 \mathrm{~m} & \text { area }=\frac{1}{2} b h=\frac{1}{2}(4)(10)=20 \mathrm{~m} & \text { area }=b h=(2)(10)=20 \mathrm{~m}
\end{array}
$
In each case, the area under the velocity-time graph equals the total distance traveled.
As we will see in the next section, the equation for displacement as a function of velocity and time is $d=v_0 t+\frac{1}{2} a t^2$, which becomes $d=\frac{1}{2} a t^2$ for an object starting at rest. If we apply this equation to each of these situations, we would get the same numbers that we got from the area under the graph:
Between 0 and $2 \mathrm{~s}$
Between 0 and $4 \mathrm{~s}$
Between $4 s$ and $6 s$
$
\begin{array}{ccc}
a=2.5 \frac{\mathrm{m}}{\mathrm{s}^2} & a=2.5 \frac{\mathrm{m}}{\mathrm{s}^2} & a=0 \\
d=\frac{1}{2}(2.5)\left(2^2\right)=5 \mathrm{~m} & d=\frac{1}{2}(2.5)\left(4^2\right)=20 \mathrm{~m} & d=v_{\text {ave. }} t=(10)(2)=20 \mathrm{~m}
\end{array}
$
What an AP Motion Graph Problem Looks Like
AP motion problems almost always involve either graphs or projectiles. Freeresponse problems will often ask you to compare two graphs, such as a positiontime graph vs. a velocity-time graph, or a velocity-time graph vs. an accelerationtime graph.
Here is an example of a free-response question involving motion graphs:
Q: A $0.50 \mathrm{~kg}$ cart moves on a straight horizontal track. The graph of velocity $v$ versus time $t$ for the cart is given below.
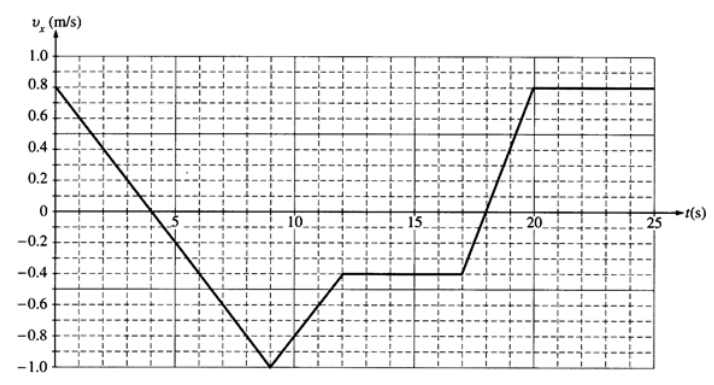
a. Indicate every time $t$ for which the cart is at rest.
The cart is at rest whenever the velocity is zero. Velocity is the $y$-axis, so we simply need to find the places where $y=0$. These are at $t=4 \mathrm{~s}$ and $t=18 \mathrm{~s}$.
b. Indicate every time interval for which the speed (magnitude of velocity) of the cart is increasing.
For the velocity vector, we use positive and negative to indicate direction. Therefore, the magnitude is the absolute value. The magnitude of the velocity is increasing whenever the graph is moving away from the $x$-axis, which happens in the intervals $4-9 \mathrm{~s}$ and $18-20 \mathrm{~s}$.
The most likely mistake would be to give the times when the acceleration is positive. Positive acceleration can mean that the speed is increasing in the positive direction, but it can also mean that it is decreasing in the negative direction.
c. Determine the horizontal position $x$ of the cart at $t=9.0 \mathrm{~s}$ if the cart is located at $x=2.0 \mathrm{~m}$ at $t=0$.
Position is the area under a velocity-time graph. Therefore, if we add the positive and subtract the negative areas from $t=0$ to $t=9.0 \mathrm{~s}$, the result is the position at $t=9.0 \mathrm{~s}$.
The area of the triangular region from $0-4 \mathrm{~s}$ is $\left(\frac{1}{2}\right)(4)(0.8)=1.6 \mathrm{~m}$.
The area of the triangular region from $4-9 \mathrm{~s}$ is $\left(\frac{1}{2}\right)(5)(-1.0)=-2.5 \mathrm{~m}$.
The total displacement is therefore $\Delta x=1.6+(-2.5)=-0.9 \mathrm{~m}$.
Because the cart’s initial position was $+2.0 \mathrm{~m}$, its final position is $2.0+(-0.9)=+1.1 \mathrm{~m}$.
The most likely mistakes would be to add the areas regardless of whether they are negative or positive, and to forget to add the initial position after you have found the displacement.
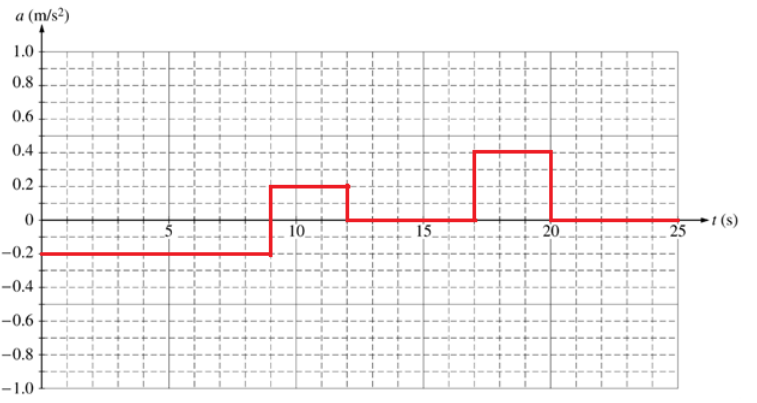
d. On the axes below, sketch the acceleration $a$ versus time $t$ graph for the motion of the cart from $t=0$ to $t=25 \mathrm{~s}$.
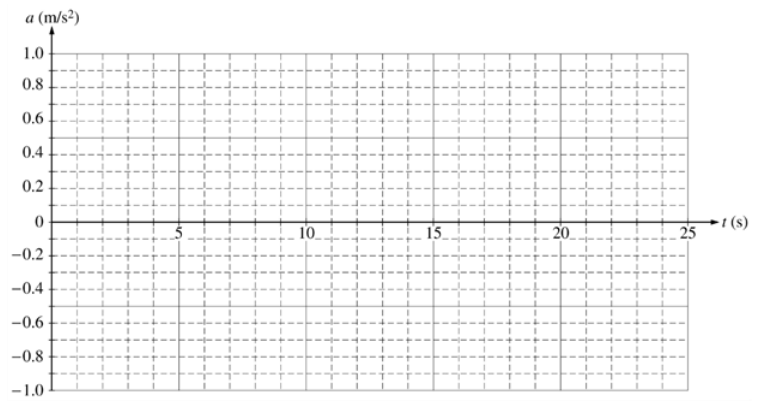
Acceleration is the slope of a velocity-time graph. Because the graph is discontininuous, we need to split it at each point where the slope suddenly changes. Each of the regions is a straight line (constant slope), which means all of the accelerations are constant (horizontal lines on the graph).
From 0-9 s, the slope is $\frac{\Delta y}{\Delta x}=\frac{-1.8}{9}=-0.2 \frac{\mathrm{m}}{\mathrm{s}^2}$.
From 9-12s, the slope is $\frac{\Delta y}{\Delta x}=\frac{+0.6}{3}=+0.2 \frac{\mathrm{m}}{\mathrm{s}^2}$.
From 12-17s and from 20-25s, the slope is zero.
From 17-20s, the slope is $\frac{\Delta y}{\Delta x}=\frac{+1.2}{3}=+0.4 \frac{\mathrm{m}}{\mathrm{s}^2}$.
The graph therefore looks like the following:
e. The original problem also included a part (e), which was a simple projectile problem (discussed later).