Topics covered in this chapter:
• Linear Momentum
•Impulse
•Conservation of Linear Momentum
• Angular Momentum
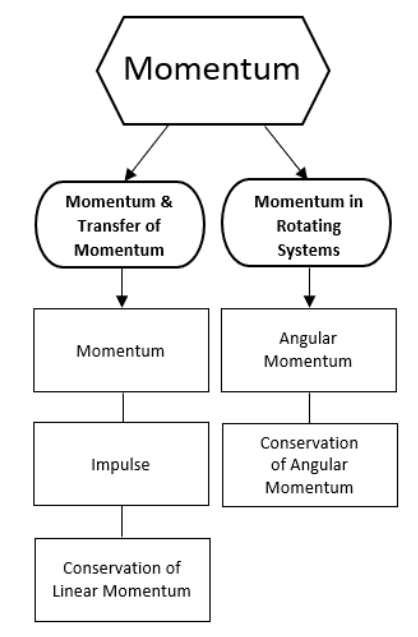
Linear Momentum
Notes:
In the $17^{\text {th }}$ century, the German mathematician Gottfried Leibnitz recognized the fact that in some cases, the mass and velocity of objects before and after a collision were related by kinetic energy $\left(\frac{1}{2} m v^2\right.$, which he called the “quantity of motion”); in other cases, however, the “quantity of motion” was not preserved but another quantity ( $m v$, which he called the “motive force”) was the same before and after. Debate about whether “quantity of motion” or “motive force” was the correct quantity to use for these types of problems continued through the $17^{\text {th }}$ and $18^{\text {th }}$ centuries.
We now realize that both quantities are relevant. “Quantity of motion” is what we now call kinetic energy, and “motive force” is what we now call momentum. The two quantities are different but related.
momentum $(\overrightarrow{\boldsymbol{p}})$ : the amount of force that a moving object could transfer in a given amount of time in a collision. (Formerly called “motive force”.)
Momentum is a vector quantity given by the formula:
$
\overrightarrow{\boldsymbol{p}}=m \overrightarrow{\boldsymbol{v}}
$
and is measured in units of $\mathrm{N} \cdot \mathrm{s}$, or $\frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}}$.
Because momentum is a vector, its sign (positive or negative) indicates its direction. An object’s momentum is in the same direction as (and therefore has the same sign as) its velocity.
An object at rest has a momentum of zero because $\vec{v}=0$.
collision: when two or more objects come together, at least one of which is moving, and make contact with each other. Momentum is always transferred in a collision.
elastic collision: when two or more objects collide and then separate.
perfectly elastic collision: when two or more objects collide and separate, and none of the kinetic energy of any of the objects is “lost” (turned into any other form of energy).
inelastic collision: when two or more objects collide and remain together. (Or when one object separates into two or more objects.)
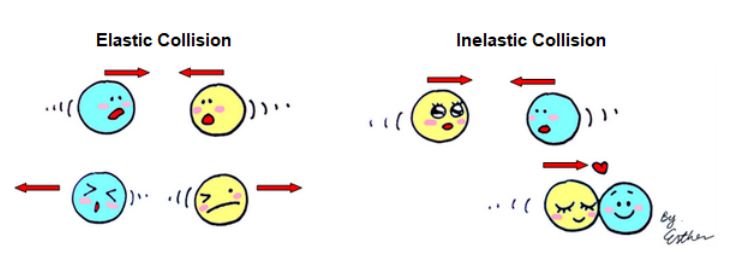
Momentum is the quantity that is transferred between objects in a collision.
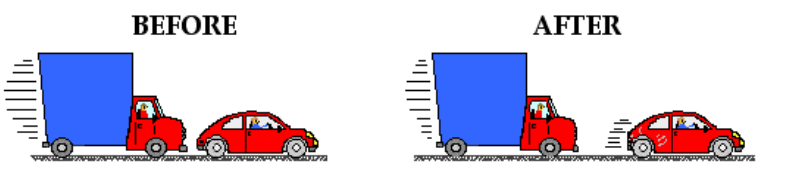
Before the above collision, the truck was moving, so it had momentum; the car was not moving, so it did not have any momentum. After the collision, some of the truck’s momentum was transferred to the car. After the collision, both vehicles were moving, which means both vehicles had momentum.
Of course, total energy is also conserved in a collision. However, the form of energy can change. Before the above collision, all of the energy in the system was the initial kinetic energy of the truck. Afterwards, some of the energy is the final kinetic energy of the truck, some of the energy is the kinetic energy of the car, but some of the energy is converted to heat, sound, etc. during the collision.
inertia: an object’s ability to resist the action of a force.
Recall that a net force causes acceleration, which means the inertia of an object is its ability to resist a change in velocity. This means that in linear (translational) systems, inertia is simply mass. In rotating systems, inertia is the moment of inertia, which depends on the mass and the distance from the center of rotation. (See Rotational Inertia on page 332.)
Inertia and momentum are related, but are not the same thing; an object has inertia even at rest, when its momentum is zero. An object’s momentum changes if either its mass or its velocity changes, but an the inertia of an object can change only if either its mass changes or its distance from the center of rotation changes.
Momentum and Kinetic Energy
We have the following equations, both of which relate mass and velocity:
momentum: $\quad \overrightarrow{\boldsymbol{p}}=m \overrightarrow{\boldsymbol{v}}$
kinetic energy: $\quad K=\frac{1}{2} m v^2$
We can combine these equations to eliminate $v$, giving the equation:
$
K=\frac{p^2}{2 m}
$
The relationship between momentum and kinetic energy explains why the velocities of objects after a collision are determined by the collision.
Because kinetic energy and momentum must both be conserved in an elastic collision, the two final velocities are actually determined by the masses and the initial velocities. The masses and initial velocities are determined before the collision. The only variables are the two velocities after the collision. This means there are two equations (conservation of momentum and conservation of kinetic energy) and two unknowns ( and $\overrightarrow{\boldsymbol{v}}_{2, f}$ ).
For a perfectly elastic collision, conservation of momentum states:
$
m_1 \overrightarrow{\mathbf{v}}_{1, i}+m_2 \overrightarrow{\mathbf{v}}_{2, i}=m_1 \overrightarrow{\mathbf{v}}_{1, f}+m_2 \overrightarrow{\mathbf{v}}_{2, f}
$
and conservation of kinetic energy states:
$
\frac{1}{2} m_1 v_{1, i}^2+\frac{1}{2} m_2 v_{2, i}^2=\frac{1}{2} m_1 v_{1, f}^2+\frac{1}{2} m_2 v_{2, f}^2
$
If we use these two equations to solve for $\vec{v}_{1, f}$ and $\overrightarrow{\boldsymbol{v}}_{2, f}$ in terms of the other variables, the result is the following:
$
\begin{gathered}
\overrightarrow{\boldsymbol{v}}_{1, f}=\frac{\overrightarrow{\boldsymbol{v}}_{1, i}\left(m_1-m_2\right)+2 m_2 \overrightarrow{\boldsymbol{v}}_{2, i}}{m_1+m_2} \\
\overrightarrow{\boldsymbol{v}}_{2, f}=\frac{\overrightarrow{\boldsymbol{v}}_{2, i}\left(m_2-m_1\right)+2 m_1 \overrightarrow{\boldsymbol{v}}_{1, i}}{m_1+m_2}
\end{gathered}
$
For an inelastic collision, there is no solution that satisfies both the conservation of momentum and the conservation of kinetic energy; the total kinetic energy after the collision is always less than the total kinetic energy before. This matches what we observe, which is that momentum is conserved, but some of the kinetic energy is converted to heat during the collision.
Newton’s Cradle
Newton’s Cradle is the name given to a set of identical balls that are able to swing suspended from wires, as shown at the right.
When one ball is swung and allowed to collide with the rest of the balls, the momentum transfers through the balls and one ball is knocked out from the opposite end. When two balls are swung, two balls are knocked out from the opposite end, and so on.
This apparatus demonstrates the relationship between the conservation of momentum and conservation of kinetic energy. When the balls collide, the collision is mostly elastic collision, meaning that all of the momentum and most of the kinetic energy are conserved.
Before the collision, the moving ball(s) have momentum ( $m v)$ and kinetic energy $\left(\frac{1}{2} m v^2\right)$. There are no external forces, which means momentum must be conserved. The collision is mostly elastic, which means kinetic eneray is mostly also conserved. The only way for the same momentum and kinetic energy to be present after the collision is for the same number of balls to swing away from the opposite end with the same velocity.
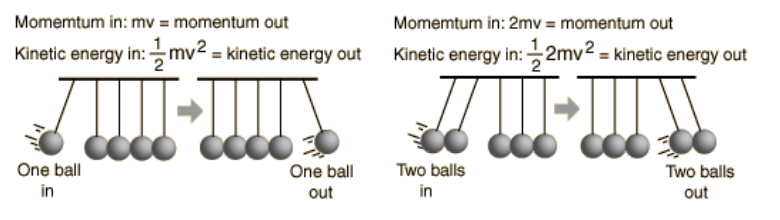
If only momentum had to be conserved, it would be possible to pull back one ball but for two balls to come out the other side at $1 / 2$ of the original velocity. However, this can’t actually happen.
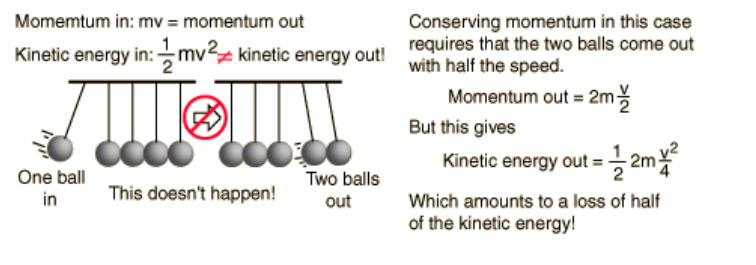
Note also that if there were no friction, the balls would continue to swing forever. However, because of friction (between the balls and air molecules, within the strings as they stretch, etc.) and conversion of some of the kinetic energy to other forms (such as heat), the balls in a real Newton’s Cradle will, of course, slow down and eventually stop.
Impulse
Notes: impulse $(\vec{J})$ : the effect of a force applied over a period of time; the accumulation of momentum.
Mathematically, impulse is a change in momentum, and is also equal to force times time:
$
\Delta \overrightarrow{\boldsymbol{p}}=\overrightarrow{\boldsymbol{J}}=\overrightarrow{\boldsymbol{F}} t \quad \text { and } \quad \overrightarrow{\boldsymbol{F}}=\frac{\overrightarrow{\boldsymbol{j}}}{t}=\frac{\Delta \overrightarrow{\boldsymbol{p}}}{t}=\frac{d \overrightarrow{\boldsymbol{p}}}{d t}
$
Where $\overrightarrow{\boldsymbol{F}}$ is the force vector and, $t$ is time.
Impulse is measured in newton-seconds (N·s), just like momentum.
Impulse is analogous to work:
– Work is a change in energy; impulse is a change in momentum.
– Work is the accumulation of force over a distance $(W=\overrightarrow{\boldsymbol{F}} \bullet \overrightarrow{\boldsymbol{d}})$; Impulse is the accumulation of force over a time $(\vec{J}=\overrightarrow{\boldsymbol{F}} t)$
Just as work is the area of a graph of force vs. distance, impulse is the area under a graph of force vs. time:
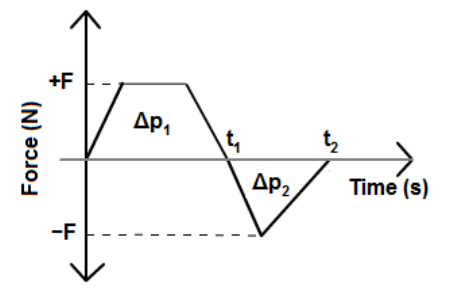
In the above graph, the impulse from time zero to $t_1$ would be $\Delta p_1$. The impulse from $t_1$ to $t_2$ would be $\Delta p_2$, and the total impulse would be $\Delta p_1+\Delta p_2$ (keeping in mind that $\Delta p_2$ is negative).
Sample Problem:
Q: A baseball has a mass of $0.145 \mathrm{~kg}$ and is pitched with a velocity of $38 \frac{\mathrm{m}}{\mathrm{s}}$ toward home plate. After the ball is hit, its velocity is $52 \frac{\mathrm{m}}{\mathrm{s}}$ in the opposite direction, toward the center field fence. If the impact between the ball and bat takes place over an interval of $3.0 \mathrm{~ms}(0.0030 \mathrm{~s})$, find the impulse given to the ball by the bat, and the force applied to the ball by the bat.
Answer/Explanation
A: The ball starts out moving toward home plate. The bat applies an impulse in the opposite direction. As with any vector quantity, opposite directions means we will have opposite signs. If we choose the initial direction of the ball (toward home plate) as the positive direction, then the initial velocity is $+38 \frac{\mathrm{m}}{\mathrm{s}}$, and the final velocity is $-52 \frac{\mathrm{m}}{\mathrm{s}}$. Because mass is scalar and always positive, this means the initial momentum is positive and the final momentum is negative.
Furthermore, because the final velocity is about $11 / 2$ times as much as the initial velocity (in the opposite direction) and the mass doesn’t change, this means the impulse needs to be enough to negate the ball’s initial momentum plus enough in addition to give the ball about 112 times as much momentum in the opposite direction.
Just like the energy bar charts that we used for conservation of energy problems, we can create a momentum bar chart. Note that because momentum is a vector that can be positive or negative, our momentum bar chart needs to be able to accommodate positive and negative values.
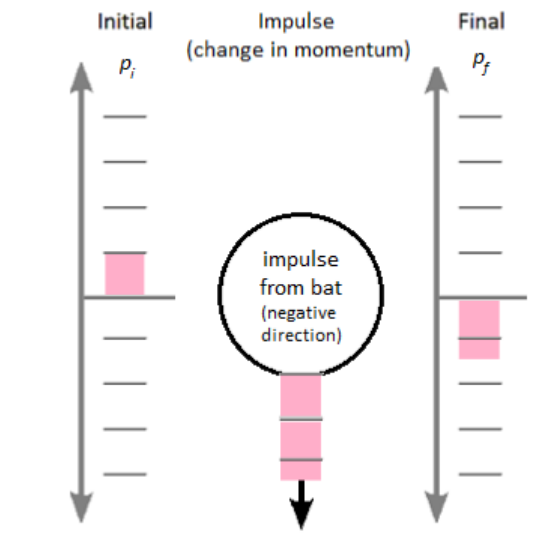
Now, solving the problem mathematically:
The negative values for force and impulse mean that they are directed toward center field, which makes sense.
Answers: $\vec{J}=13.05 \mathrm{~N} \cdot$ s toward center field; $\vec{F}=4350 \mathrm{~N}$ toward center field
Conservation of Linear Momentum
Notes:
collision: when two or more objects come together and hit each other.
elastic collision: a collision in which the objects bounce off each other (remain separate) after they collide, without any loss of kinetic energy.
inelastic collision: a collision in which the objects remain together after colliding. In an inelastic collision, total energy is still conserved, but some of the energy is changed into other forms, so the amount of kinetic energy is different before vs. after the collision.
Any macroscopic collision (meaning a collision between objects that are larger than individual atoms or molecules) will convert some of the kinetic energy into internal energy and other forms of energy. This means that no large-scale impacts are ever perfectly elastic.
Conservation of Momentum
Recall that in physics, if a quantity is “conserved”, that means when some change happens to a system, there is the same amount of that quantity after the change as there was before.
In a closed system, momentum is conserved. This means that unless there is an outside force, the combined momentum of all of the objects after they collide is equal to the combined momentum of all of the objects before the collision.
As we did with conservation of energy problems, we can use a momentum bar chart to show changes in momentum before and after a collision.
The following momentum bar chart is for an elastic collision. Imagine that two objects are moving in opposite directions and then collide. Before the collision, the first object has a momentum of $+3 \mathrm{~N} \cdot \mathrm{s}$, and the second has a momentum of $-1 \mathrm{~N} \cdot \mathrm{s}$. The total momentum is therefore $+3+(-1)=+2 \mathrm{~N} \cdot \mathrm{s}$.
After the collision, the first object has a momentum of $+1.5 \mathrm{~N} \cdot \mathrm{s}$ and the second has a momentum of $+0.5 \mathrm{~N} \cdot \mathrm{s}$. Because there are no forces changing the momentum of the system, the final momentum must also be $+2 \mathrm{~N} \cdot \mathrm{s}$.
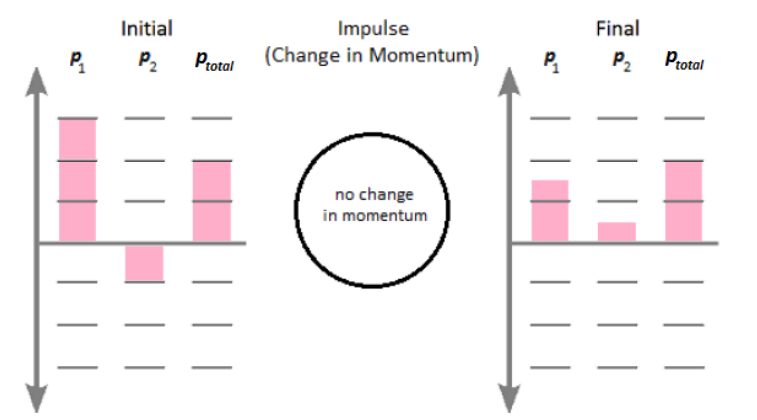
The following momentum bar chart is for an inelastic collision. Imagine that two objects are moving in the same direction, and then collide. Before the collision, the first object has a momentum of $+1 \mathrm{~N} \cdot \mathrm{s}$, and the second has a momentum of $+3 \mathrm{~N} \cdot \mathrm{s}$. The total momentum is therefore $+1+(+3)=+4 \mathrm{~N} \cdot \mathrm{s}$.
After the collision, the objects remain together, so the total momentum must still be +4 N.s.
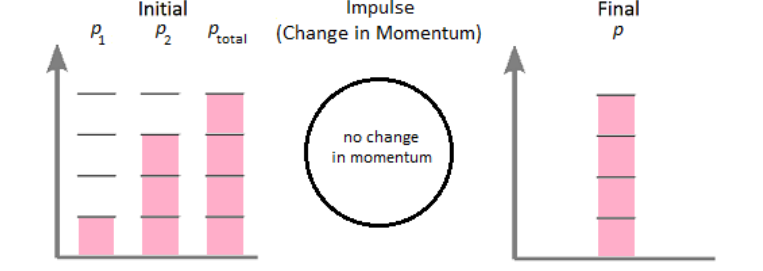
Solving Conservation of Momentum Problems
Almost all momentum problems involve the conservation of momentum law:
$
\begin{aligned}
\text { Before }+ \text { Impulse } & =\text { After } \\
\sum \overrightarrow{\boldsymbol{p}}_i+\overrightarrow{\boldsymbol{J}} & =\sum \overrightarrow{\boldsymbol{p}}_f \\
\sum \overrightarrow{\boldsymbol{p}}_i+\Delta \overrightarrow{\boldsymbol{p}} & =\sum \overrightarrow{\boldsymbol{p}}_f
\end{aligned}
$
The symbol $\sum$ is the Greek capital letter “sigma”. In mathematics, the symbol $\sum$ means “summation”. $\sum \vec{p}$ means the sum of the momentums. The subscript ” $i$ ” means initial (before the collision), and the subscript ” $f$ ” means final (after the collision). In plain English, $\sum \overrightarrow{\boldsymbol{p}}$ means find each individual value of $\overrightarrow{\boldsymbol{p}}$ (positive or negative, depending on the direction) and then add them all up to find the total.
In plain English, the conservation of momentum law means that the total momentum before a collision, plus any momentum that we add (impulse), must be equal to the total momentum after.
Note that most momentum problems do not mention the word “momentum.” The problems usually give information about masses and velocities before and after some sort of collision, and it is up to you to realize that the problem involves conservation of momentum.
Most momentum problems involve collisions. In most of the problems that we will see in this course, there will be two objects, and the objects will either bounce off each other (elastic collision) or remain together (inelastic collision).
Elastic Collisions
For example, if you have an elastic collision between two objects and no added impulse, the law of conservation of momentum is:
$
\text { Before(+ Impulse) } \begin{aligned}
& =\text { After } \\
\sum \overrightarrow{\boldsymbol{p}}_i+0 & =\sum \overrightarrow{\boldsymbol{p}}_f \\
\overrightarrow{\boldsymbol{p}}_{1, i}+\overrightarrow{\boldsymbol{p}}_{2, i} & =\overrightarrow{\boldsymbol{p}}_{1, f}+\overrightarrow{\boldsymbol{p}}_{2, f}
\end{aligned}
$
Notice that we have two subscripts after each ” $\overrightarrow{\boldsymbol{p}}$ ” and each ” $\overrightarrow{\boldsymbol{v}}$ “, because we have two separate things to keep track of. The “i” and ” $f$ ” mean “initial” and “final,” and the ” 1 ” and “2” mean object \#1 and object \#2.
Because $\overrightarrow{\boldsymbol{p}}=m \overrightarrow{\boldsymbol{v}}$, we can replace each $\overrightarrow{\boldsymbol{p}}$ with $m \overrightarrow{\boldsymbol{v}}$, giving:
$
\begin{aligned}
\text { Before } & =\text { After } \\
\sum \overrightarrow{\boldsymbol{p}}_i & =\sum \overrightarrow{\boldsymbol{p}}_f \\
\overrightarrow{\boldsymbol{p}}_{1, i}+\overrightarrow{\boldsymbol{p}}_{2, i} & =\overrightarrow{\boldsymbol{p}}_{1, f}+\overrightarrow{\boldsymbol{p}}_{2, f} \\
m_1 \overrightarrow{\boldsymbol{v}}_{1, i}+m_2 \overrightarrow{\boldsymbol{v}}_{2, i} & =m_1 \overrightarrow{\boldsymbol{v}}_{1, f}+m_2 \overrightarrow{\boldsymbol{v}}_{2, f}
\end{aligned}
$
Note that there are six separate quantities in this problem: the two masses $\left(m_1 \& m_2\right)$, the two initial velocities $\left(\overrightarrow{\boldsymbol{v}}_{1, i} \& \vec{v}_{2, i}\right)$, and the two final velocities $\left(\vec{v}_{1, f} \& \vec{v}_{2, f}\right)$. A typical momentum problem will give you (or enable you to calculate) all but one of these, and will ask you for the last one.
Inelastic Collisions
For an inelastic collision between two objects, the objects stick together after the collision, which means either there is only one “object” afterwards, or there is only one object at the beginning and it separates. The total mass of the object is $m_T=m_1+m_2$, and when the objects are together, there is only one velocity.
The law of conservation of momentum for an inelastic collision (with no impulse) is:
This time there are five quantities: the two masses $\left(m_1 \& m_2\right)$, and either the two initial velocities $\left(\vec{v}_{1, i} \& \overrightarrow{\boldsymbol{v}}_{2, i}\right)$, and the final velocity $\left(\overrightarrow{\boldsymbol{v}}_f\right)$; or the initial velocity $\left(\vec{v}_i\right)$ and the two final velocities $\left(\vec{v}_{1, f} \& \overrightarrow{\boldsymbol{v}}_{2, f}\right)$.
Again, a typical momentum problem will give you (or enable you to calculate) all but one of these, and will ask you for the last one. To solve this problem, you will also need to add the masses to find $m_T$.
Sample Problems:
Q: An object with a mass of $8.0 \mathrm{~kg}$ moving with a velocity of $+5.0 \frac{\mathrm{m}}{\mathrm{s}}$ collides with a stationary object with a mass of $12 \mathrm{~kg}$. If the two objects stick together after the collision, what is their velocity?
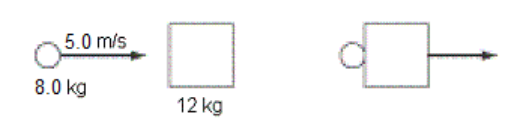
Answer/Explanation
A: The momentum of the moving object before the collision is:
$
\overrightarrow{\boldsymbol{p}}=m \overrightarrow{\boldsymbol{v}}=(8.0)(+5.0)=+40 \mathrm{~N} \cdot \mathrm{s}
$
The stationary object has a momentum of zero, so the total momentum of the two objects combined is $+40 \mathrm{~N} \cdot \mathrm{s}$.
After the collision, the total mass is $8.0 \mathrm{~kg}+12 \mathrm{~kg}=20 \mathrm{~kg}$. The momentum after the collision must still be $+40 \mathrm{~N} \cdot \mathrm{s}$, which means the velocity is:
$
\overrightarrow{\boldsymbol{p}}=m \overrightarrow{\boldsymbol{v}} \quad 40=20 \vec{v} \quad \vec{v}=+2 \frac{m}{\mathrm{~s}}
$
Using the equation, we would solve this as follows:
$
\begin{aligned}
\text { Before } & =\text { After } \\
\overrightarrow{\boldsymbol{p}}_{1, i}+\overrightarrow{\boldsymbol{p}}_{2, i} & =\overrightarrow{\boldsymbol{p}}_f \\
m_1 \overrightarrow{\boldsymbol{v}}_{1, i}+m_2 \overrightarrow{\boldsymbol{v}}_{2, i} & =m_T \overrightarrow{\boldsymbol{v}}_f \\
(8)(5)+(12)(0) & =(8+12) \overrightarrow{\boldsymbol{v}}_f \\
40 & =20 \overrightarrow{\boldsymbol{v}}_f \\
\overrightarrow{\boldsymbol{v}}_f & =\frac{40}{20}=+2 \frac{\mathrm{m}}{\mathrm{s}}
\end{aligned}
$
Angular Momentum
Notes:
angular momentum $(\vec{L})$ : the momentum of a rotating object in the direction of rotation. Angular momentum is the property of an object that resists changes in the speed or direction of rotation. Angular momentum is measured in units of $\frac{\mathrm{kg} \cdot \mathrm{m}^2}{\mathrm{~s}}$.
Just as linear momentum is the product of mass (linear inertia) and (linear) velocity, angular momentum is also the product of the moment of inertia (rotational inertia) and angular (rotational) velocity:
” $\mathrm{CP} 1$ and honors physics students are responsible only for a qualitative understanding of angular momentum. AP ${ }^{\circledast}$ Physics students need to solve quantitative problems.
Angular momentum can also be converted to linear momentum, and vice versa. Angular momentum is the cross-product of radius and linear momentum:
$
\overrightarrow{\boldsymbol{L}}=\overrightarrow{\boldsymbol{r}} \times \overrightarrow{\boldsymbol{p}}=r p \sin \theta
$
E.g., if you shoot a bullet into a door:
1. As soon as the bullet embeds itself in the door, it is constrained to move in an arc, so the linear momentum of the bullet becomes angular momentum.
2. The total angular momentum of the bullet just before impact equals the total angular momentum of the bullet and door after impact.
Just as a force produces a change in linear momentum, a torque produces a change in angular momentum. The net external torque on an object is its change in angular momentum with respect to time:
$
\overrightarrow{\boldsymbol{\tau}}_{n e t}=\frac{\Delta \overrightarrow{\boldsymbol{L}}}{t}=\frac{d \overrightarrow{\boldsymbol{L}}}{d t} \quad \text { and } \quad \Delta \overrightarrow{\boldsymbol{L}}=\overrightarrow{\boldsymbol{\tau}}_{n e t} t
$
Conservation of Angular Momentum
Just as linear momentum is conserved unless an external force is applied, angular momentum is conserved unless an external torque is applied. This means that the total angular momentum before some change (that occurs entirely within the system) must equal the total angular momentum after the change.
An example of this occurs when a person spinning (e.g., an ice skater) begins the spin with arms extended, then pulls the arms closer to the body. This causes the person to spin faster. (In physics terms, it increases the angular velocity, which means it causes angular acceleration.)
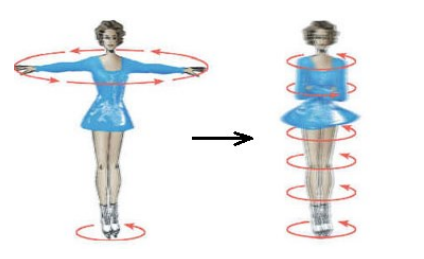
When the skater’s arms are extended, the moment of inertia of the skater is greater (because there is more mass farther out) than when the arms are close to the body. Conservation of angular momentum tells us that:
$
\begin{aligned}
L_i & =L_f \\
I_i \omega_i & =I_f \omega_f
\end{aligned}
$
I.e., if $I$ decreases, then $\omega$ must increase.
Another popular example, which shows the vector nature of angular momentum, is the demonstration of a person holding a spinning bicycle wheel on a rotating chair. The person then turns over the bicycle wheel, causing it to rotate in the opposite direction:
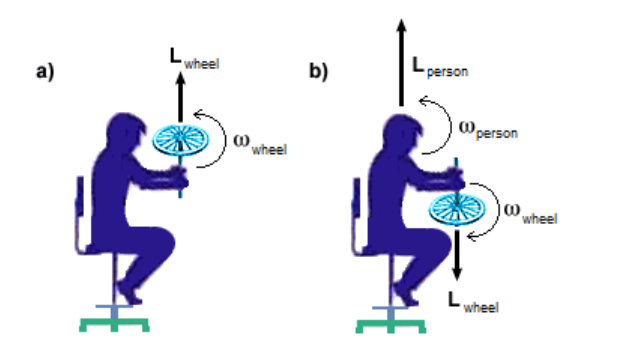Initially, the direction of the angular momentum vector of the wheel is upwards.
When the person turns over the wheel, the angular momentum of the wheel reverses direction. Because the person-wheel-chair system is an isolated system, the total angular momentum must be conserved. This means the person must rotate in the opposite direction as the wheel, so that the total angular momentum (magnitude and direction) of the person-wheel-chair system remains the same as before.
Sample Problem:
Q: A “Long-Playing” (LP) phonograph record has a radius of $15 \mathrm{~cm}$ and a mass of 150 g. A typical phonograph could accelerate an LP from rest to its final speed in $0.35 \mathrm{~s}$.
a. Calculate the angular momentum of a phonograph record (LP) rotating at $33 \frac{1}{3}$ RPM.
b. What average torque would be exerted on the LP?
Answer/Explanation
A: The angular momentum of a rotating body is $L=I \omega$. This means we need to find $I$ (the moment of inertia) and $\omega$ (the angular velocity).
An LP is a solid disk, which means the formula for its moment of inertia is:
$
\begin{aligned}
& I=\frac{1}{2} m r^2 \\
& I=\left(\frac{1}{2}\right)(0.15 \mathrm{~kg})(0.15 \mathrm{~m})^2=1.69 \times 10^{-3} \mathrm{~kg} \cdot \mathrm{m}^2 \\
& \omega=\frac{33 \frac{1}{3} \mathrm{rev}}{1 \mathrm{~min}} \times \frac{1 \mathrm{~min}}{60 \mathrm{~s}} \times \frac{2 \pi \mathrm{rad}}{1 \mathrm{rev}}=3.49 \frac{\mathrm{rad}}{\mathrm{s}} \\
& L=I \omega \\
& L=\left(1.69 \times 10^{-3} \mathrm{~kg} \cdot \mathrm{m}^2\right)\left(3.49 \frac{\mathrm{rad}}{\mathrm{s}}\right) \\
& L=5.89 \times 10^{-3} \frac{\mathrm{kg} \cdot \mathrm{m}^2}{\mathrm{~s}} \\
& \tau=\frac{\Delta L}{\Delta t}=\frac{L-L_o}{\Delta t}=\frac{5.89 \times 10^{-3}-0}{0.35}=1.68 \times 10^{-2} \mathrm{~N} \cdot \mathrm{m}
\end{aligned}
$