Topics covered in this chapter:
Centripetal Force
Notes:
As we saw previously, when an object is moving at a constant speed around a circle, its direction keeps changing toward the center of the circle as it goes around, which means there is continuous acceleration toward the center of the circle.
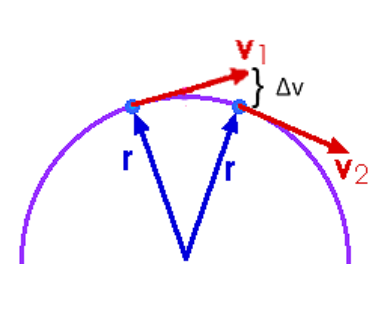
Because acceleration is caused by a net force (Newton’s second law of motion), if there is continuous acceleration toward the center of the circle, then there must be a continuous force toward the center of the circle.
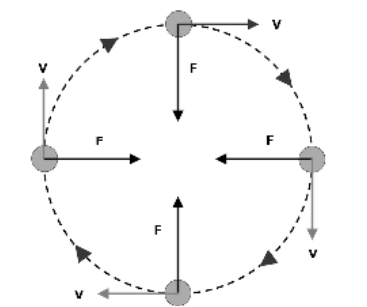
This force is called “centripetal force”.
centripetal force: the inward force that keeps an object moving in a circle. If the centripetal force were removed, the object would fly away from the circle in a straight line that starts from a point tangent to the circle.
Recall that the equation ${ }^*$ for centripetal acceleration $\left(a_c\right)$ is:
$
a_c=\frac{v^2}{r}=r \omega^2
$
Given that $F=m a$, the equation for centripetal force is therefore:
$
F_c=m a_c=\frac{m v^2}{r}=m r \omega^2
$
If you are in the reference frame of the object that is moving in a circle, you are being accelerated toward the center of the circle. You feel a force that appears to be pushing or pulling you away from the center of the circle. This is called “centrifugal force”.
centrifugal force: the outward force felt by an object that is moving in a circle.
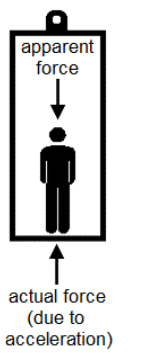
Centrifugal force is called a “fictitious force” because it does not exist in an inertial reference frame. However, centrifugal force does exist in a rotating reference frame; it is the inertia of objects resisting acceleration as they are continuously pulled toward the center of a circle by centripetal acceleration.
This is the same as the feeling of increased weight that you feel when you are in an elevator and it starts to move upwards (which is also a moving reference frame). An increase in the normal force from the floor because of the upward acceleration of the elevator feels the same as an increase in the downward force of gravity.
(due to acceleration)
” Recall that centripetal motion and centripetal force relates to angular/rotational motion and forces (which are studied in APФ Physics but not in the CP1 or honors courses).
Equations or portions of equations with angular velocity $(\omega)$ and angular acceleration $(\alpha)$ apply only to the $\mathrm{AP}^{\oplus}$ course.
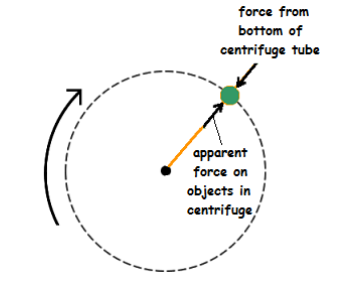
Similarly, a sample being spun in a centrifuge is subjected to the force from the bottom of the centrifuge tube as the tube is accelerated toward the center.
The faster the rotation, the stronger the force. An increase in the normal force from the bottom of the centrifuge tube would feel like a downward force in the reference frame of the centrifuge tube.
Sample Problems:
Question
Q: A $300 \mathrm{~kg}$ roller coaster car reaches the bottom of a hill traveling at a speed of $20 \frac{\mathrm{m}}{\mathrm{s}}$. If the track curves upwards with a radius of $50 \mathrm{~m}$, what is the total force exerted by the track on the car?
Answer/Explanation
A: The total force on the car is the normal force needed to resist the force of gravity on the car (equal to the weight of the car) plus the centripetal force exerted on the car as it moves in a circular path.
$
\begin{aligned}
& F_g=m g=(300)(10)=3000 \mathrm{~N} \\
& F_c=\frac{m v^2}{r}=\frac{(300)(20)^2}{50}=2400 \mathrm{~N} \\
& F_N=F_g+F_c=3000+2400=5400 \mathrm{~N}
\end{aligned}
$
Question
Q: A $20 \mathrm{~g}$ ball attached to a $60 \mathrm{~cm}$ long string is swung in a horizontal circle 80 times per minute. Neglecting gravity, what is the tension in the string?
Answer/Explanation
A: Converting to MKS units, the mass of the ball is $0.02 \mathrm{~kg}$ and the string is $0.6 \mathrm{~m}$ long.
We can solve this two ways: we can convert revolutions either to meters by multiplying by $2 \pi r$, or to radians by multiplying by $2 \pi$ :
$
\begin{aligned}
& \omega=\frac{80 \text { revolutions }}{1 \mathrm{~min}} \times \frac{(2 \pi)(0.60 \mathrm{~m})}{1 \text { revelution }} \times \frac{1 \mathrm{~min}}{60 \mathrm{~s}}=\frac{96 \pi \mathrm{m}}{60 \mathrm{~s}}=5.03 \frac{\mathrm{m}}{\mathrm{s}} \\
& F_T=F_c=\frac{m v^2}{r}=\frac{(0.02)(5.03)^2}{0.6}=0.842 \mathrm{~N} \\
& \omega=\frac{80 \text { revolutions }}{1 \mathrm{~min}} \times \frac{2 \pi \text { rad }}{1 \text { revolution }} \times \frac{1 \mathrm{~min}}{60 \mathrm{~s}}=\frac{160 \pi \mathrm{rad}}{60 \mathrm{~s}}=8.38 \frac{\mathrm{rad}}{\mathrm{s}} \\
& F_T=F_c=m r \omega^2 \\
& F_T=F_c=(0.02)(0.6)(8.38)^2=0.842 \mathrm{~N}
\end{aligned}
$
Center of Mass
Notes:center of mass: the point where all of an object’s mass could be placed without changing the overall forces on the object or its rotational inertia.
Objects have nonzero volumes. For any object, some of the mass of the object will always be closer to the center of rotation, and some of the mass will always be farther away. In most of the problems that you will see in this course, we can simplify the problem by pretending that all of the mass of the object is at a single point.
You can find the location of the center of mass of an object from the following formula:
$
r_{c m}=\frac{\sum_i m_i r_i}{\sum_i m_i}
$
In this equation, the symbol $\sum$ means “summation.” When this symbol appears in a math equation, calculate the equation to the right of the symbol for each set of values, then add them up.
In this case, for each object (designated by a subscript), first multiply $m r$ for that object, and then add up each of these products to get the numerator. Add up the masses to get the denominator. Then divide.
Because an object at rest remains at rest, this means that an object’s center of mass is also the point at which the object will balance on a sharp point. (Actually, because gravity is involved, the object balances because the torques around the center of mass cancel. We will discuss that in detail later.)

Finally, note that an object that is rotating freely in space will always rotate about its center of mass:

Sample Problem:
Q: Two people sit at the ends of a massless $3.5 \mathrm{~m}$ long seesaw. One person has a mass of $59 \mathrm{~kg}$, and the other has a mass of $71 \mathrm{~kg}$. Where is their center of mass?
Answer/Explanation
A: (Yes, there’s no such thing as a massless seesaw. This is an idealization to make the problem easy to solve.)
In order to make this problem simple, let us place the 59-kg person at a distance of zero.
$
\begin{aligned}
& r_{c m}=\frac{\sum_i m_i r_i}{\sum_i m_i} \\
& r_{c m}=\frac{(59)(0)+(71)(3.5)}{(59+71)} \\
& r_{c m}=\frac{248.5}{130}=1.91 \mathrm{~m}
\end{aligned}
$
Their center of mass is $1.91 \mathrm{~m}$ away from the $59-\mathrm{kg}$ person.
Rotational Inertia
Notes:
inertia: the tendency for an object to continue to do what it is doing (remain at rest or remain in motion).
rotational inertia (or angular inertia): the tendency for a rotating object to continue rotating.
moment of inertia $(I)$ : a quantitative measure of the rotational inertia of an object. Moment of inertia is measured in units of $\mathrm{kg} \cdot \mathrm{m}^2$. Inertia in linear systems is a fairly easy concept to understand. The more mass an object has, the more it tends to remain at rest or in motion, and the more force is required to change its motion. I.e., in a linear system, inertia depends only on mass.
Rotational Inertia
Rotational inertia is somewhat more complicated than the inertia in a non-rotating system. Suppose we have a mass that is being rotated at the end of a string. (Let’s imagine that we’re doing this in space, so we can neglect the effects of gravity.) The mass’s inertia keeps it moving around in a circle at the same speed. If you suddenly shorten the string, the mass continues moving at the same speed through the air, but because the radius is shorter, the mass makes more revolutions around the circle in a given amount of time.
In other words, the object has the same linear speed (not the same velocity because its direction is constantly changing), but its angular velocity (degrees per second) has increased.
This must mean that an object’s moment of inertia (its tendency to continue moving at a constant angular velocity) must depend on its distance from the center of rotation as well as its mass.
The formula for moment of inertia is:
$
I=\sum_i m_i r_i^2
$
I.e., for each object or component (designated by a subscript), first multiply $m r^2$ for the object and then add up the rotational inertias for each of the objects to get the total.
For a point mass (a simplification that assumes that the entire mass exists at a single point):
$
I=m r^2
$
This means the rotational inertia of the point-mass is the same as the rotational inertia of the object.
Calculating the moment of inertia for an arbitrary shape requires calculus.
However, for solid, regular objects with well-defined shapes, their moments of inertia can be reduced to simple formulas:
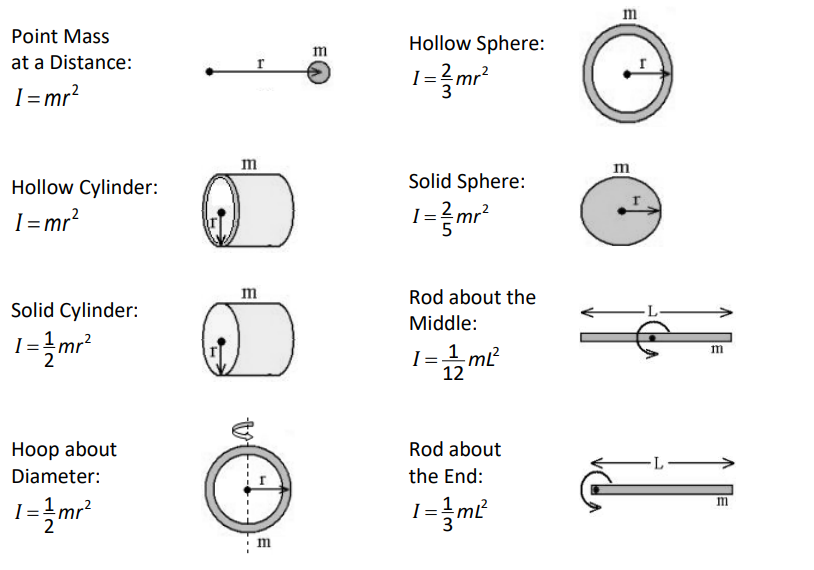
In the above table, note that a rod can have a cross-section of any shape; for example a door hanging from its hinges is considered a rod rotated about the end for the purpose of determining its moment of inertia.
Sample Problem:
Q: A solid brass cylinder has a density of $8500 \frac{\mathrm{kg}}{\mathrm{m}^3}$, a radius of $0.10 \mathrm{~m}$ and a height of $0.20 \mathrm{~m}$ and is rotated about its center. What is its moment of inertia?
Answer/Explanation
A: In order to find the mass of the cylinder, we need to use the volume and the density.
$
\begin{gathered}
V=\pi r^2 h=(3.14)(0.1)^2(0.2) \\
V=0.00628 \mathrm{~m}^3 \\
\rho=\frac{m}{V} \\
8500=\frac{m}{0.00628} \\
m=53.4 \mathrm{~kg}
\end{gathered}
$
Now that we have its mass, we can find
the moment of inertia of the cylinder:
$
I=\frac{1}{2} m r^2
$
$
I=\frac{1}{2}(53.4)(0.1)^2=0.534 \mathrm{~kg} \cdot \mathrm{m}^2
$
Parallel Axis Theorem
The moment of inertia of any object about an axis through its center of mass is always the minimum moment of inertia for any axis in that direction in space.
The moment of inertia about any axis that is parallel to the axis through the center of mass is given by:
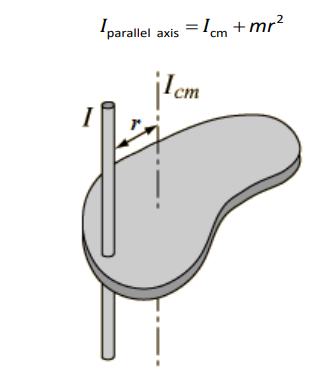
Note that the formula for the moment of inertia of a point mass at a distance $r$ from the center of rotation comes from the parallel axis theorem. The radius of the point mass itself is zero, which means:
$
\begin{gathered}
I_{c m}=0 \\
I=I_{c m}+m r^2 \\
I=0+m r^2
\end{gathered}
$
The parallel axis theorem is used in $A P^{\oplus}$ Physics $\mathrm{C}$ : Mechanics, but is outside the scope of this course.
Torque
Notes: torque $(\overrightarrow{\boldsymbol{\tau}})$ : a vector quantity that measures the effectiveness of a force in causing rotation. Take care to distinguish the Greek letter ” $\tau$ ” from the Roman letter ” $\mathrm{t}$ “. Torque is measured in units of newton-meters:
$
1 \mathrm{~N} \cdot \mathrm{m}=1 \frac{\mathrm{kg} \cdot \mathrm{m}^2}{\mathrm{~s}^2}
$
Note that work and energy (which we will study later) are also measured in newton-meters. However, work and energy are different quantities from torque, and are not interchangeable. (Among other differences, work and energy are scalar quantities, and torque is a vector quantity.)
axis of rotation: the point around which an object rotates.
fulcrum: the point around which a lever pivots. Also called the pivot.
lever arm: the distance from the axis of rotation that a force is applied, causing a torque.
Just as force is the quantity that causes linear acceleration, torque is the quantity that causes a change in the speed of rotation (rotational acceleration).
Because inertia is a property of mass, Newton’s second law is the relationship between force and inertia. Newton’s second law in rotational systems looks similar to Newton’s second law in linear systems:
$
\begin{array}{cc}
\overrightarrow{\boldsymbol{a}}=\frac{\sum \overrightarrow{\boldsymbol{F}}}{m}=\frac{\overrightarrow{\boldsymbol{F}}_{n e t}}{m} & \overrightarrow{\boldsymbol{\alpha}}=\frac{\sum \overrightarrow{\boldsymbol{\tau}}}{I}=\frac{\overrightarrow{\boldsymbol{\tau}}_{\text {net }}}{I} \\
\overrightarrow{\boldsymbol{F}}_{\text {net }}=m \overrightarrow{\boldsymbol{a}} & \overrightarrow{\boldsymbol{\tau}}_{\text {net }}=I \overrightarrow{\boldsymbol{\alpha}}^* \\
\text { linear } & \text { rotational }
\end{array}
$
As you should remember, a net force of zero, that means all forces cancel in all directions and there is no acceleration. If there is no acceleration $(\vec{a}=0)$, the velocity remains constant (which may or may not equal zero).
Similarly, if the net torque is zero, then the torques cancel in all directions and there is no angular acceleration. If there is no angular acceleration $(\vec{\alpha}=0)$, then the angular velocity remains constant (which may or may not equal zero).
rotational equilibrium: when all of the torques on an object cancel each other’s effects (resulting in a net force of zero) and the object either does not rotate or rotates with a constant angular velocity.
Torque is also the cross product of distance from the center of rotation (“lever arm”) $\times$ force:
$\overrightarrow{\mathbf{\tau}}=\overrightarrow{\mathbf{r}} \times \overrightarrow{\mathbf{F}} \quad$ which gives: $\quad\|\overrightarrow{\mathbf{\tau}}\|=\tau=r F \sin \theta=r F_{\perp}$
where $\theta$ is the angle between the lever arm and the applied force.
We use the variable $r$ for the lever arm (which is a distance) because torque causes rotation, and $r$ is the distance from the center of the circle (radius) at which the force is applied.
$F \sin \theta$ is sometimes written as $F_{\perp}$ (the component of the force that is perpendicular to the radius) and sometimes $F_{\|}$(the component of the force that is parallel to the direction of motion). These notes will use $F_{\perp}$, because in many cases the force is applied to a lever, and the component of the force that causes the torque is perpendicular to the lever itself, so it is easy to think of it as “the amount of force that is perpendicular to the lever”. This gives the equation:
$
\tau=r F_{\perp}
$
Of course, because torque is the cross product of two vectors, it is a vector whose direction is perpendicular to both the lever arm and the force.
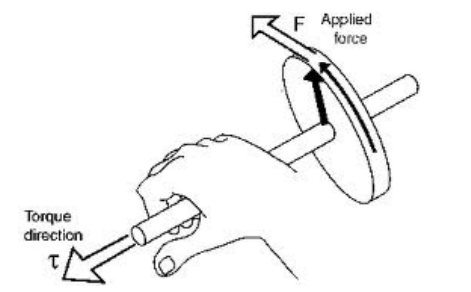
This is an application of the “right hand rule.” If your fingers of your right hand curl from the first vector $(\overrightarrow{\boldsymbol{r}})$ to the second $(\overrightarrow{\boldsymbol{F}})$, then your thumb points in the direction of the resultant vector $(\overrightarrow{\boldsymbol{\tau}})$. Note that the direction of the torque vector is parallel to the axis of rotation.
Note, however, that you can’t “feel” torque; you can only “feel” force. Most people think of the “direction” of a torque as the direction of the rotation that the torque would produce (clockwise or counterclockwise). In fact, the College Board usually uses this convention.
Mathematically, the direction of the torque vector is needed only to give torques a positive or negative sign, so torques in the same direction add and torques in opposite directions subtract. In practice, most people find it easier to define the positive direction for rotation (clockwise $U$ or counterclockwise $U$ ) and use those for positive or negative torques in the problem, regardless of the direction of the torque vector.
Sample Problem:
Q: If a perpendicular force of $20 \mathrm{~N}$ is applied to a wrench with a $25 \mathrm{~cm}$ handle, what is the torque applied to the bolt?
Answer/Explanation
$
\text { A: } \begin{aligned}
\tau & =r F_{\perp} \\
\tau & =(0.25 \mathrm{~m})(20 \mathrm{~N}) \\
\tau & =4 \mathrm{~N} \cdot \mathrm{m}
\end{aligned}
$
Seesaw Problems
A seesaw problem is one in which objects on opposite sides of a lever (such as a seesaw) balance one another.
To solve seesaw problems, if the seesaw is not moving, then the torques must balance and the net torque must be zero.
The total torque on each side is the sum of the separate torques caused by the separate masses. Each of these masses can be considered as a point mass (infinitely small object) placed at the object’s center of mass.
Sample Problems:
Q: A 100 cm meter stick is balanced at its center (the 50-cm mark) with two objects hanging from it, as shown below:
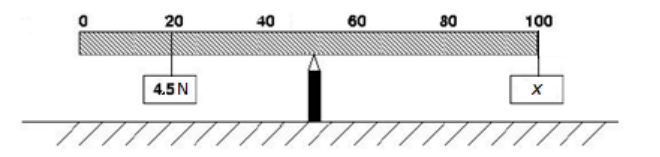
One of the objects weighs $4.5 \mathrm{~N}$, and is hung from the $20-\mathrm{cm}$ mark $(30 \mathrm{~cm}=0.3 \mathrm{~m}$ from the fulcrum). A second object is hung at the opposite end (50 cm $=0.5 \mathrm{~m}$ from the fulcrum). What is the weight of the second object?
Answer/Explanation
A: In order for the ruler to balance, the torque on the left side (which is trying to rotate the ruler counter-clockwise) must be equal to the torque on the right side (which is trying to rotate the ruler clockwise). The torques from the two halves of the ruler are the same (because the ruler is balanced in the middle), so this means the torques applied by the objects also must be equal.
The torque applied by the object on the left is:
$
\tau=r F=(0.30)(4.5)=1.35 \mathrm{~N} \cdot \mathrm{m}
$
The torque applied by the object on the right must also be $1.35 \mathrm{~N} \cdot \mathrm{m}$, so we can calculate the force:
$
\begin{aligned}
& \tau=r F \\
& 1.35=0.50 F \\
& F=\frac{1.35}{0.50}=2.7 \mathrm{~N}
\end{aligned}
$
Solving Linear & Rotational Force/Torque Problems
Notes:
Newton’s second law – that forces produce acceleration-applies in both linear and rotational contexts. In fact, you can think of the equations as exactly the same, except that one set uses Cartesian coördinates, and the other uses polar or spherical coördinates.
You can substitute rotational variables for linear variables in all of Newton’s equations (motion and forces), and the equations are still valid.
Problems Involving Linear and Rotational Dynamics
The main points of the linear Dynamics (Forces) \& Gravitation chapter were:
a. A net force produces acceleration. $\overrightarrow{\boldsymbol{F}}_{\text {net }}=m \overrightarrow{\boldsymbol{a}}$
b. If there is no acceleration, then there is no net force, which means all forces must cancel in all directions. No acceleration may mean a static situation (nothing is moving) or constant velocity.
c. Forces are vectors. Perpendicular vectors do not affect each other, which means perpendicular forces do not affect each other.
The analogous points hold true for torques:
1. A net torque produces angular acceleration. $\overrightarrow{\boldsymbol{\tau}}_{n e t}=I \overrightarrow{\boldsymbol{\alpha}}$
2. If there is no angular acceleration, then there is no net torque, which means all torques must cancel. No angular acceleration may mean a static situation (nothing is rotating) or it may mean that there is rotation with constant angular velocity.
3. Torques are vectors. Perpendicular torques do not affect each other.
4. Torques and linear forces act independently.
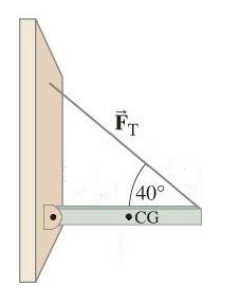
One of the most common types of problem involves a stationary object that has both linear forces and torques, both of which are in balance.
In the diagrams at the right, a beam with a center of gravity (center of mass) in the middle (labeled “CG”) is attached to a wall with a hinge. The end of the beam is held up with a rope at an angle of $40^{\circ}$ above the horizontal.
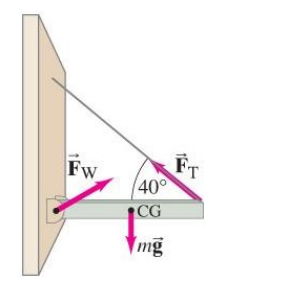
The rope applies a torque to the beam at the end at an angle of rotation with a radius equal to the length of the beam. Gravity applies a force straight down on the beam.
1. Because the beam is not rotating, we know that $\overrightarrow{\boldsymbol{\tau}}_{\text {net }}$ must be zero, which means the wall must apply a torque that counteracts the torque applied by the rope. (Note that the axis of rotation for the torque from the wall is the opposite end of the beam.)
2. Because the beam is not moving (translationally), we know that $\overrightarrow{\boldsymbol{F}}_{n e t}$ must be zero in both the vertical and horizontal directions. This means that the wall must apply a force $\overrightarrow{\boldsymbol{F}}_w$ to balance the vertical and horizontal components of $\overrightarrow{\boldsymbol{F}}_T$ and $m \overrightarrow{\boldsymbol{g}}$. Therefore, the vertical component of $\overrightarrow{\boldsymbol{F}}_W$ plus the vertical component of $\overrightarrow{\boldsymbol{F}}_T$ must add up to $m \overrightarrow{\boldsymbol{g}}$, and the horizontal components of $\overrightarrow{\boldsymbol{F}}_T$ and $\overrightarrow{\boldsymbol{F}}_W$ must cancel.
AP questions often combine pulleys with torque. (See the section on Tension starting on page 274.) These questions usually require you to combine the following concepts/equations:
1. A torque is the action of a force acting perpendicular to the radius at some distance from the axis of rotation: $\tau=r F_{\perp}$
2. Net torque produces angular acceleration according to the formula:
$
\tau_{\text {net }}=I \alpha
$
3. The relationships between tangential and angular velocity and acceleration are: $v_T=r \omega$ and $a_T=r \alpha \leftarrow$ Memorize these!
AP free-response problems are always scaffolded, meaning that each part leads to the next.