Topics covered in this chapter:
This chapter discusses the physics of simple harmonic (repetitive) motion.
• Simple Harmonic Motion (SHM) describes the concept of repetitive back-andforth motion and situations that apply to it.
• Springs and Pendulums describe specific examples of SHM and the specific equations relating to each.
Simple Harmonic Motion
Notes:
simple harmonic motion: motion consisting of regular, periodic back-and-forth oscillation.
Requirements:
•The acceleration is always in the opposite direction from the displacement. This means the acceleration always slows down the motion and reverses the direction.
•In an ideal system (no friction), once simple harmonic motion is started, it would continue forever.
• A graph of displacement vs. time will result in the trigonometric function sine or cosine.
Examples of Simple Harmonic Motion
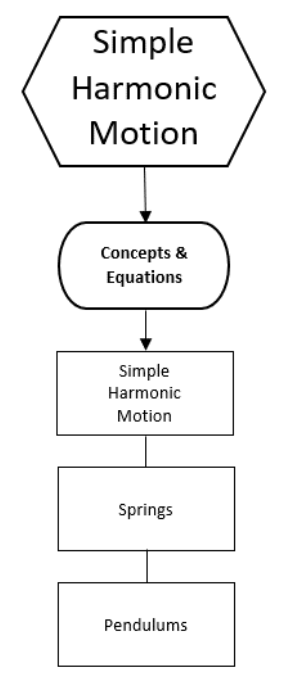
• Springs; as the spring compresses or stretches, the spring force accelerates it back toward its equilibrium position.
• Pendulums: as the pendulum swings, gravity accelerates it back toward its equilibrium position.
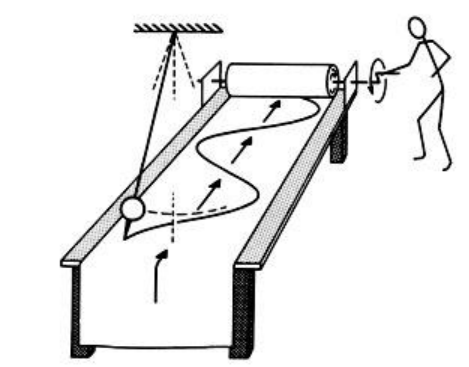
• Waves: waves passing through some medium (such as water or air) cause the medium to oscillate up and down, like a duck sitting on the water as waves pass by.
• Uniform circular motion: as an object moves around a circle, its vertical position (y -position) is continuously oscillating between +r and –r.
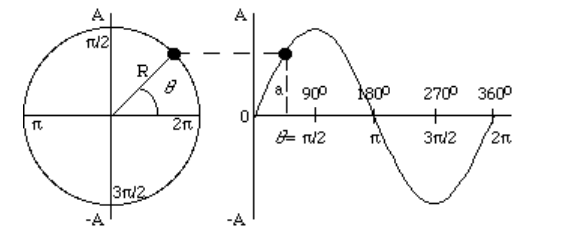
Kinematics of Simple Harmonic Motion
As you can see from the uniform circular motion graph above, the $y$-position of an object in simple harmonic motion as a function of time is the function sine or cosine of the angle around the circle, depending on where you declare the starting position to be. From calculus, the general equations of periodic or oscillating motion are therefore:
position: $\quad x=A \cos (\omega t+\phi)$
velocity: $\quad v=-A \omega \sin (\omega t+\phi)=\frac{d x}{d t}$
acceleration: $a=-A \omega^2 \cos (\omega t+\phi)=\frac{d v}{d t}=\frac{d^2 x}{d t^2}$
Where:
$\begin{aligned} x & =\text { displacement from the equilibrium point } x=0 \\ A & =\text { amplitude (maximum displacement) } \\ \omega & =\text { angular frequency } \\ t & =\text { time } \\ \phi & =\text { phase angle (offset) }\end{aligned}$
The phase angle $\phi$ or offset is the position where the cycle starts, relative to the equilibrium (zero) point.
Because many simple harmonic motion problems (including $A P^{\oplus}$ problems) are given in terms of the frequency of oscillation (number of oscillations per second), we can multiply the angular frequency by $2 \pi$ to use $f$ instead of $\omega$, i.e., $\omega=2 \pi f$.
On the $A P^{\oplus}$ formula sheet, $\phi$ is assumed to be zero, resulting in the following version of the position equation:
$
x=A \cos (2 \pi f t)
$
You are expected to be able to understand and use the position equation above, but simple harmonic problems that involve velocity and acceleration equations are beyond the scope of this course and have not been seen on the $A^{\oplus}$ exam.
* The derivatives $\frac{d x}{d t}, \frac{d v}{d t}$, and $\frac{d^2 x}{d t^2}$ are from calculus. The velocity and acceleration equations are beyond the scope of the $A P^{\oplus}$ Physics course.
Springs
Notes:
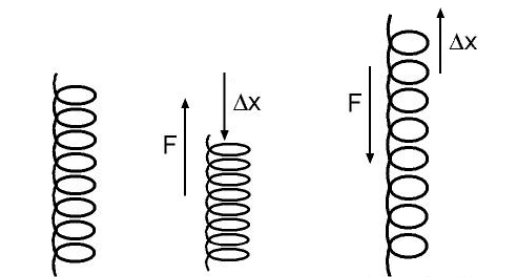
spring: a coiled object that resists motion parallel with the direction of propagation of the coil.
Spring Force
The equation for the force (vector) from a spring is given by Hooke’s Law, named for the British physicist Robert Hooke:
$
\overrightarrow{\boldsymbol{F}}_{\mathrm{s}}=-k \overrightarrow{\boldsymbol{x}}
$
Where $\overrightarrow{\boldsymbol{F}}_{\mathrm{s}}$ is the spring force (vector quantity representing the force exerted by the spring), $\overrightarrow{\boldsymbol{x}}$ is the displacement of the end of the spring (also a vector quantity), and $k$ is the spring constant, an intrinsic property of the spring based on its mass, thickness, and the elasticity of the material that it is made of.
The negative sign in the equation is because the force is always in the opposite (negative) direction from the displacement.
A Slinky has a spring constant of $0.5 \frac{\mathrm{N}}{\mathrm{m}}$, while a heavy garage door spring might have a spring constant of $500 \frac{\mathrm{N}}{\mathrm{m}}$.
Potential Energy
The potential energy stored in a spring is given by the equation:
$
U=\frac{1}{2} k x^2
$
Where $U$ is the potential energy (measured in joules), $k$ is the spring constant, and $x$ is the displacement. Note that the potential energy is always positive (or zero); this is because energy is a scalar quantity. A stretched spring and a compressed spring both have potential energy.
The Period of a Spring
period or period of oscillation: the time it takes a spring to move from its maximum displacement in one direction to its maximum displacement in the opposite direction and back again. The variable for the period is $T$, and the unit is usually seconds.
The period of a spring depends on the mass of the spring and its spring constant, and is given by the equation:
$
T_s=2 \pi \sqrt{\frac{m}{k}}
$
Frequency
frequency: the number of times something occurs in a given amount of time. Frequency is usually given by the variable $f$, and is measured in units of hertz $(\mathrm{Hz})$. One hertz is the inverse of one second:
$
1 \mathrm{~Hz} \equiv \frac{1}{1 \mathrm{~s}} \equiv 1 \mathrm{~s}^{-1}
$
Note that period and frequency are reciprocals of each other:
$
T=\frac{1}{f} \quad \text { and } \quad f=\frac{1}{T}
$
Sample Problem:
Q: A spring with a mass of $0.1 \mathrm{~kg}$ and a spring constant of $2.7 \frac{\mathrm{N}}{\mathrm{m}}$ is compressed $0.3 \mathrm{~m}$. Find the force needed to compress the spring, the potential energy stored in the spring when it is compressed, and the period of oscillation.
Answer/Explanation
A: The force is given by Hooke’s Law.
Substituting these values gives:
$
\begin{aligned}
& \overrightarrow{\boldsymbol{F}}=-k \overrightarrow{\boldsymbol{x}} \\
& \overrightarrow{\boldsymbol{F}}=-\left(2.7 \frac{N}{\mathrm{~m}}\right)(+0.3 \mathrm{~m})=-0.81 \mathrm{~N}
\end{aligned}
$
The potential energy is:
$
\begin{aligned}
& U=\frac{1}{2} k x^2 \\
& U=(0.5)\left(2.7 \frac{N}{m}\right)(0.3 \mathrm{~m})^2=0.12 \mathrm{~J}
\end{aligned}
$
The period is:
$
\begin{aligned}
& T_s=2 \pi \sqrt{\frac{m}{k}} \\
& T_s=(2)(3.14) \sqrt{\frac{0.1}{2.7}} \\
& T_s=6.28 \sqrt{0.037}=(6.28)(0.19)=1.2 \mathrm{~s}
\end{aligned}
$
Pendulums
Notes: pendulum: a lever that is suspended from a point such that it can swing back and forth.
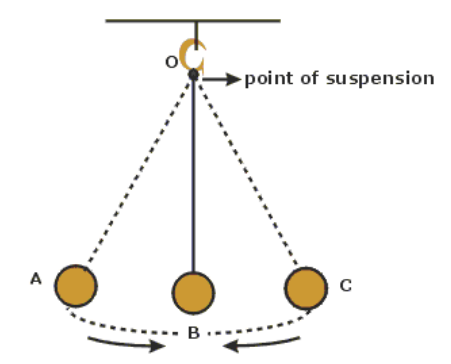
The Forces on a Pendulum
As the pendulum swings, its mass remains constant, which means the force of gravity pulling it down remains constant. The tension on the pendulum (which we can think of as a rope or string, though the pendulum can also be solid) also remains constant as it swings.
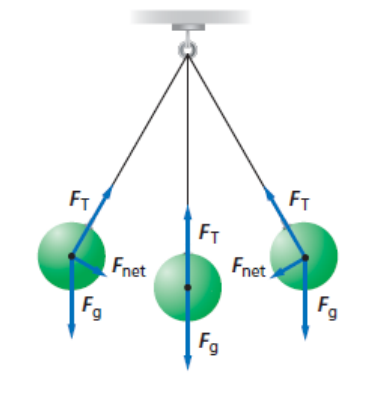
However, as the pendulum swings, the angle of the tension force changes. When the pendulum is not in the center (bottom), the vertical component of the tension is $F_{\mathrm{T}} \cos \theta$, and the horizontal component is $F_{\mathrm{T}} \sin \theta$. Because the angle is between $0^{\circ}$ and $90^{\circ}, \cos \theta<1$, which means $F_{\mathrm{g}}$ is greater than the upward component of $F_{\mathrm{T}}$. This causes the pendulum to eventually stop. Also because the angle is between $0^{\circ}$ and $90^{\circ}, \sin \theta>0$, This causes the pendulum to start swinging in the opposite direction.
The Period of a Pendulum
period or period of oscillation: the time it takes a pendulum to travel from its maximum displacement in one direction to its maximum displacement in the opposite direction and back again. The variable for the period is $T$, and the unit is usually seconds.
Note that the time between pendulum “beats” (such as the tick-tock of a pendulum clock) are $1 / 2$ of the period of the pendulum. Thus a “grandfather” clock with a pendulum that beats seconds has a period $T=2 \mathrm{~s}$.
The period of a pendulum depends on the force of gravity, the length of the pendulum, and the maximum angle of displacement. For small angles $\left(\theta<15^{\circ}\right)$, the period is given by the equation:
$
T=2 \pi \sqrt{\frac{\ell}{g}}
$
where $T$ is the period of oscillation, $\ell$ is the length of the pendulum in meters, and $g$ is the acceleration due to gravity (approximately $10 \frac{\mathrm{m}}{\mathrm{s}^2}$ on Earth).
Note that the potential energy of a pendulum is simply the gravitational potential energy of the pendulum’s center of mass.
The velocity of the pendulum at its lowest point (where the potential energy is zero and all of the energy is kinetic) can be calculated using conservation of energy.
Sample Problem:
Q: An antique clock has a pendulum that is $0.20 \mathrm{~m}$ long. What is its period?
Answer/Explanation
A: The period is given by the equation:
$
\begin{aligned}
T & =2 \pi \sqrt{\frac{\ell}{g}} \\
T & =2(3.14) \sqrt{\frac{0.20}{10}} \\
T & =6.28 \sqrt{0.02} \\
T & =(6.28)(0.141) \\
T & =0.889 \mathrm{~s}
\end{aligned}
$