Topics covered in this chapter:
- Radioactive Decay
- Nuclear Equations
- Mass Defect & Binding Energy
- Half-Life
- Nuclear Fission & Fusion
- Practical Uses for Nuclear Radiation
Radioactive Decay
Notes:
nuclear instability: When something is unstable, it is likely to change. If the nucleus of an atom is unstable, changes can occur that affect the number of protons and neutrons in the atom.
Note that when this happens, the nucleus ends up with a different number of protons. This causes the atom to literally turn into an atom of a different element. When this happens, the physical and chemical properties instantaneously change into the properties of the new element!
radioactive decay: the process by which the nucleus of an atom changes, transforming the element into a different element or isotope.
nuclear equation: an equation describing (through chemical symbols) what happens to an atom as it undergoes radioactive decay.
Causes of Nuclear Instability
Two of the causes of nuclear instability are:
Size
Because the strong force acts over a limited distance, when nuclei get too large (more than 82 protons), it is no longer possible for the strong force to keep the nucleus together indefinitely. The form of decay that results from an atom exceeding its stable size is called alpha $(\alpha)$ decay.
The Weak Nuclear Force
The weak force is caused by the exchange (absorption and/or emission) of $W$ and $Z$ bosons. This causes a down quark to change to an up quark or vice-versa. The change of quark flavor has the effect of changing a proton to a neutron, or a neutron to a proton. (Note that the action of the weak force is the only known way of changing the flavor of a quark.) The form of decay that results from the action of the weak force is called beta ( $B)$ decay.
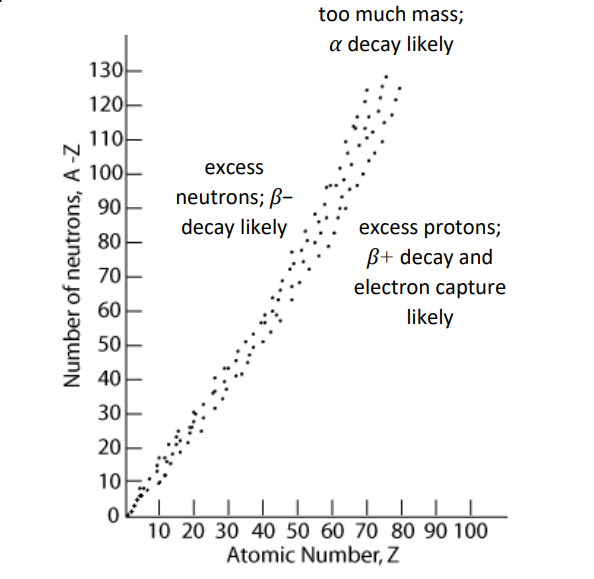
band of stability: isotopes with a ratio of protons to neutrons that results in a stable nucleus (one that does not spontaneously undergo radioactive decay). This observation suggests that the ratio of up to down quarks within the nucleus is somehow involved in preventing the weak force from causing quarks to change flavor.
alpha $(\alpha)$ decay: a type of radioactive decay in which the nucleus loses two protons and two neutrons (an alpha particle). An alpha particle is a ${ }_2^4 \mathrm{He}^{2+}$ ion (the nucleus of a helium-4 atom), with two protons, a mass of $4 \mathrm{amu}$, and a charge of +2. For example:
$
{ }_{92}^{238} \mathrm{U} \rightarrow{ }_{90}^{234} \mathrm{Th}+{ }_2^4 \mathrm{He}
$
Atoms are most likely to undergo alpha decay if they have an otherwise stable proton/neutron ratio but a large atomic number.
Alpha decay has never been observed in atoms with an atomic number less than 52 (tellurium), and is rare in elements with an atomic number less than 73 (tantalum).
Net effects of $\alpha$ decay:
- Atom loses 2 protons and 2 neutrons (atomic number goes down by 2 and mass number goes down by 4$)$
- An $\alpha$ particle (a ${ }_2^4 \mathrm{He}^{+2}$ ion) is ejected from the nucleus at high speed.
beta minus $(\beta-)$ decay: a type of radioactive decay in which a neutron is converted to a proton and the nucleus ejects a high speed electron $\left({ }_{-1}^0 e\right)$.
Note that a neutron consists of one up quark and two down quarks (udd), and a proton consists of two up quarks and one down quark (uud). When $\beta$-decay occurs, the weak force causes one of the quarks changes its flavor from down to up, which causes the neutron (uud) to change into a proton (udd). Because a proton was gained, the atomic number increases by one. However, because the proton used to be a neutron, the mass number does not change. For example:
$
{ }_{15}^{32} \mathrm{P} \rightarrow{ }_{16}^{32} \mathrm{~S}+{ }_{-1}^0 e
$
Atoms are likely to undergo $\beta$-decay if they have too many neutrons and not enough protons to achieve a stable neutron/proton ratio. Almost all isotopes that are heavier than isotopes of the same element within the band of stability (because of the “extra” neutrons) undergo $\beta$ – decay.
Net effects of $\beta$ – decay:
- Atom loses 1 neutron and gains 1 proton (atomic number goes up by 1 ; mass number does not change)
- A $\beta$-particle (an electron) is ejected from the nucleus at high speed.
Note that a $\beta$ – particle is assigned an atomic number of -1 . This does not mean an electron is some sort of “anti-proton”. The -1 is just used to make the equation for the number of protons work out in the nuclear equation.
beta plus $(\beta+)$ decay: a type of radioactive decay in which a proton is converted to a neutron and the nucleus ejects a high speed antielectron (positron, ${ }_{+1}^0 e$ ).
With respect to the quarks, $\beta+$ decay is the opposite of $\beta$-decay When $\beta+$ decay occurs, one of the quarks changes its flavor from up to down, which changes the proton (uud) into a neutron (udd). Because a proton was lost, the atomic number decreases by one. However, because the neutron used to be a proton, the mass number does not change. For example:
$
{ }_{12}^{23} \mathrm{Mg} \rightarrow{ }_{11}^{23} \mathrm{Na}+{ }_{+1}^0 \mathrm{e}
$
Atoms are likely to undergo $\beta+$ decay if they have too many protons and not enough neutrons to achieve a stable neutron/proton ratio. Almost all isotopes that are lighter than the isotopes of the same element that fall within the band of stability (“not enough neutrons”) undergo $\beta+$ decay.
Net effects of $\beta+$ decay:
- Atom loses 1 proton and gains 1 neutron (atomic number goes down by 1 ; mass number does not change)
- $\mathrm{A} \beta+$ particle (an antielectron or positron) is ejected from the nucleus at high speed.
electron capture (sometimes called “K-capture”): when the nucleus of the atom “captures” an electron from the innermost shell (the K-shell) and incorporates it into the nucleus. This process is exactly the reverse of $\beta$-decay; during electron capture, a quark changes flavor from up to down, which changes a proton (uud) into a neutron (udd):
$
{ }_{12}^{23} \mathrm{Mg}+{ }_{-1}^0 e \rightarrow{ }_{11}^{23} \mathrm{Na}
$
Note that $\beta+$ decay and electron capture produce the same products. Electron capture can sometimes (but not often) occur without $\beta+$ decay. However, $\beta+$ decay is always accompanied by electron capture.
Atoms are likely to undergo electron capture (and usually also $\beta+$ decay) if they have too many protons and not enough neutrons to achieve a stable neutron/proton ratio. Almost all isotopes that are lighter than the isotopes of the same element that fall within the band of stability undergo electron capture, and usually also $\beta+$ decay.
Net effects of electron capture:
- An electron is absorbed by the nucleus.
- Atom loses 1 proton and gains 1 neutron (atomic number goes down by 1; mass number does not change)
gamma $(\gamma)$ rays: most radioactive decay produces energy. Some of that energy is emitted in the form of gamma rays, which are very high energy photons of electromagnetic radiation. (Radio waves, visible light, and X-rays are other types of electromagnetic radiation.) Because gamma rays are waves (which have no mass), they can penetrate far into substances and can do a lot of damage.
Because gamma rays are not particles, emission of gamma rays does not change the composition of the nucleus.
All of the types of radioactive decay mentioned in these notes also produce $\gamma$ rays. This means to be complete, we would add gamma radiation to each of the radioactive decay equations described above:
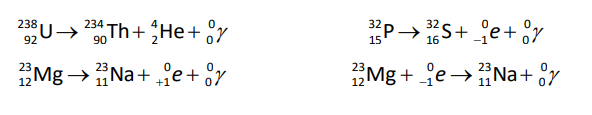
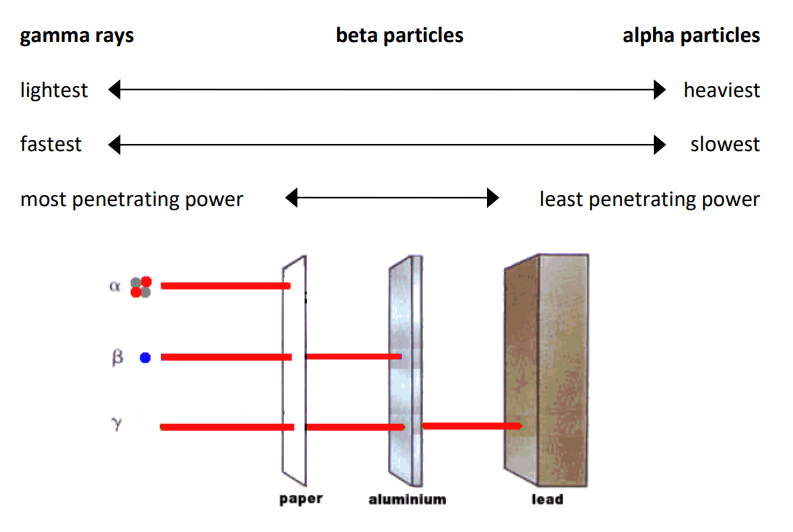
Note also that denser substances (such as lead) do a better job of blocking and absorbing radioactive emissions. This is why lead is commonly used as shielding for experiments involving radioactive substances.
Nuclear Equations
Notes:
nuclear equation: a chemical equation describing the process of an isotope undergoing radioactive decay. For example:
$
{ }_{92}^{238} \mathrm{U} \rightarrow{ }_{90}^{234} \mathrm{Th}+{ }_2^4 \mathrm{He}
$
In a nuclear equation, the number of protons (atomic number) and the total mass (mass number) are conserved on both sides of the arrow. If you look at the bottom (atomic) numbers, and replace the arrow with an = sign, you would have the following:
$
92=90+2
$
Similarly, if you look at the top (mass) numbers, and replace the arrow with an = sign, you would have:
$
238=234+4
$
Sample problems:
Q: What are the products of beta-minus $(\beta-)$ decay of ${ }^{131} I$ ?
Answer/Explanation
A: A $\beta$ – particle is an electron, which we write as ${ }_{-1}^0 e$ in a nuclear equation. This means ${ }^{131} \mathrm{I}$ decays into some unknown particle plus ${ }_{-1}^0 e$. The equation is:
$
{ }_{53}^{131} \mathrm{I} \rightarrow{ }_p^m X+{ }_{-1}^0 e
$
We can write the following equations for the atomic and mass numbers:
Atomic \#s: $53=p+-1 \rightarrow p=54$; therefore $X$ is $X e$
Mass \#s: $\quad 131=m+0 \rightarrow m=131$
Therefore, particle $X$ is ${ }_{54}^{131} X e$ So our final answer is:
The two products of decay in this reaction are ${ }_{54}^{131} \mathrm{Xe}$ and ${ }_{-1}^0 e$.
Qus: Which particle was produced in the following radioactive decay reaction:
$
{ }_{86}^{212} \mathrm{Rn} \rightarrow{ }_{84}^{208} \mathrm{Po}+{ }_p^m X
$
Answer/Explanation
Ans: The two equations are:
Atomic \#s: $86=84+p \rightarrow p=2$; therefore $X$ is $\mathrm{He}$
Mass \#s: $\quad 212=208+m \rightarrow m=4$
Therefore, particle $X$ is ${ }_2^4 \mathrm{He}$, which means it is an $\alpha$ particle.
Mass Defect & Binding Energy
Notes:
mass defect: the difference between the actual mass of an atom, and the sum of the masses of the protons, neutrons, and electrons that it contains. The mass defect is the amount of “missing” mass that was turned into binding energy.
- proton has a mass of $1.6726 \times 10^{-27} \mathrm{~kg}=1.0073 \mathrm{amu}$
- A neutron has a mass of $1.6749 \times 10^{-27} \mathrm{~kg}=1.0087 \mathrm{amu}$
- An electron has a mass of $9.1094 \times 10^{-31} \mathrm{~kg}=0.0005486 \mathrm{amu}$
To calculate the mass defect, total up the masses of each of the protons, neutrons, and electrons in an atom. The actual (observed) atomic mass of the atom is always less than this number. The “missing mass” is called the mass defect.
binding energy: the energy that holds the nucleus of an atom together through the strong nuclear force
The binding energy comes from the small amount of mass (the mass defect) that was turned into a large amount of energy, given by the equation:
$
E=m c^2
$
where $E$ is the binding energy, $m$ is the mass defect, and $c$ is the speed of light $\left(3 \times 10^8 \frac{\mathrm{m}}{\mathrm{s}}\right)$, which means $c^2$ is $9 \times 10^{16} \frac{\mathrm{m}^2}{\mathrm{~s}^2}$ (a very large number)!
You can figure out how much energy is produced by spontaneous radioactive decay by calculating the difference in the sum of the binding energies of the atoms before and after the decay.
Sample problem:
Q: Calculate the mass defect of 1 mole of uranium-238.
Answer/Explanation
A: ${ }_{92}^{238} \mathrm{U}$ has 92 protons, 146 neutrons, and 92 electrons. This means the total mass of one atom of ${ }_{92}^{238} \mathrm{U}$ should theoretically be:
92 protons $\times 1.0073 \mathrm{amu}=92.6704 \mathrm{amu}$
146 neutrons $\times 1.0087 \mathrm{amu}=147.2661 \mathrm{amu}$
92 electrons $\times 0.0005486 \mathrm{amu}=0.0505 \mathrm{amu}$
$92.6704+147.2661+0.0505=239.9870 \mathrm{amu}$
The actual observed mass of one atom of ${ }_{92}^{238} \mathrm{U}$ is $238.0003 \mathrm{amu}$.
The mass defect of one atom of ${ }_{92}^{238} \mathrm{U}$ is therefore $239.9870-238.0003=1.9867 \mathrm{amu}$.
One mole of ${ }_{92}^{238} \mathrm{U}$ would have a mass of $238.0003 \mathrm{~g}$, and therefore a total mass defect of $1.9867 \mathrm{~g}$, or $0.0019867 \mathrm{~kg}$.
Because $E=m c^2$, that means the binding energy of one mole of ${ }_{92}^{238} \mathrm{U}$ is:
$
0.0019867 \mathrm{~kg} \times\left(3.00 \times 10^8\right)^2=1.79 \times 10^{14} \mathrm{~J}
$
In case you don’t realize just how large that number is, the binding energy of just $238 \mathrm{~g}$ (1 mole) of ${ }_{92}^{238} \mathrm{U}$ would be enough energy to heat every house on Earth for an entire winter!
Half-Life
Notes:
The atoms of radioactive elements are unstable, and they spontaneously decay (change) into atoms of other elements.
For any given atom, there is a certain probability, $P$, that it will undergo radioactive decay in a given amount of time. The half-life, $\tau$, is how much time it would take to have a $50 \%$ probability of the atom decaying. If you start with $n$ atoms, after one half-life, half of them $(0.5 n)$ will have decayed.
If we start with $32 \mathrm{~g}$ of ${ }^{53} \mathrm{Fe}$, which has a half-life $(\tau)$ of 8.5 minutes, we would observe the following:
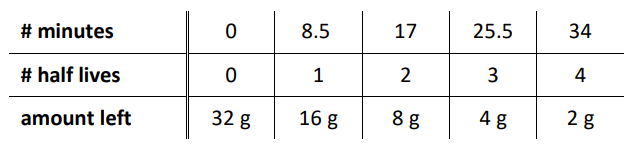
Amount of Material Remaining
Most half-life problems in a first-year high school physics course involve a whole number of half-lives and can be solved by making a table like the one above. However, on the $A^{\circledR}{ }^{\circledR}$ exam you can expect problems that do not involve a whole number of half-lives, and you need to use the exponential decay equation.
Because $n$ is decreasing, the number of atoms (and consequently also the mass) remaining after any specific period of time follows the exponential decay function:
$
A=A_o\left(\frac{1}{2}\right)^n
$
where $A$ is the amount you have now, $A_o$ is the amount you started with, and $n$ is the number of half-lives that have elapsed.
Because the number of half-lives equals the total time elapsed $(t)$ divided by the half-life $(\tau)$, we can replace $n=t / \tau$ and rewrite the equation as:
$
A=A_o\left(\frac{1}{2}\right)^{t / \tau} \text { or } \frac{A}{A_o}=\left(\frac{1}{2}\right)^{t / \tau}
$
If you want to find either $A$ or $A_o$, you can plug the values for $t$ and $\tau$ into the above equation.
Sample Problem:
Q: If you start with $228 \mathrm{~g}$ of ${ }^{90} \mathrm{Sr}$, how much would remain after 112.4 years?
Answer/Explanation
A: $A_0=228 \mathrm{~g}$
$
A=\mathrm{A}
$
$\tau=28.1$ years (from the “Selected Radioisotopes” table in your reference tables) $t=112.4$ years
$
\begin{aligned}
& A=A_0\left(\frac{1}{2}\right)^{t / t} \\
& A=(228)\left(\frac{1}{2}\right)^{112.4 / 28.1} \\
& A=(228)\left(\frac{1}{2}\right)^4 \\
& A=(228)\left(\frac{1}{16}\right) \\
& A=14.25 \mathrm{~g}
\end{aligned}
$
Or, if the decay happens to occur over an integer number of half-lives (as in this example), you can use a chart:
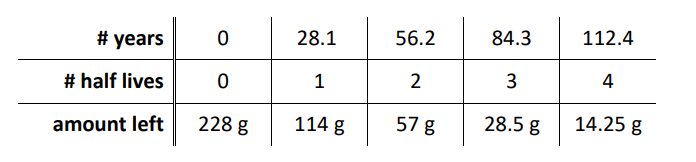
Finding the Time that has Passed
Integer Number of Half-Lives:
If the amount you started with divided by the amount left is an exact power of two, you have an integer number of half-lives and you can just make a table.
Sample problem:
Q: If you started with $64 \mathrm{~g}$ of ${ }^{131} \mathrm{I}$, how long would it take until there was only $4 \mathrm{~g}$ remaining? The half-life $(\tau)$ of ${ }^{131} \mathrm{I}$ is 8.07 days.
Answer/Explanation
A: $\frac{64}{4}=16$ which is a power of 2 , so we can simply make a table:
$
\begin{array}{|r|c|c|c|c|c|}
\hline \text { # half lives } & 0 & 1 & 2 & 3 & 4 \\
\hline \begin{array}{r}
\text { amount } \\
\text { remaining }
\end{array} & 64 \mathrm{~g} & 32 \mathrm{~g} & 16 \mathrm{~g} & 8 \mathrm{~g} & 4 \mathrm{~g} \\
\hline
\end{array}
$
From the table, after 4 half-lives, we have $4 \mathrm{~g}$ remaining.
The half-life $(\tau)$ of ${ }^{131} \mathrm{I}$ is 8.07 days.
$
8.07 \times 4=32.3 \text { days }
$
Non-Integer Number of Half-Lives
If you need to find the elapsed time and it is not an exact half-life, you need to use logarithms.
In mathematics, the only reason you ever need to use logarithms is when you need to solve for a variable that’s in an exponent. For example, suppose we have the expression of the form $a^b=c$.
If $b$ is a constant, we can solve for either $a$ or $c$, as in the expressions:
$
\begin{gathered}
a^3=21 \quad\left(\sqrt[3]{a^3}=\sqrt[3]{21}=2.76\right) \\
6^2=c \quad\left(6^2=36\right)
\end{gathered}
$
However, we can’t do this if $a$ and $c$ are constants and we need to solve for $b$, as in the expression:
$
3^b=17
$
To solve for $b$, we need to get $b$ out of the exponent. We do this by taking the logarithm of both sides:
$
\begin{gathered}
b \log (3)=\log (17) \\
b=\frac{\log (17)}{\log (3)} \\
b=\frac{1.23}{0.477}=2.58
\end{gathered}
$
It doesn’t matter which base you use. For example, using In instead of log gives the same result:
$
\begin{gathered}
b \ln (3)=\ln (17) \\
b=\frac{\ln (17)}{\ln (3)} \\
b=\frac{2.83}{1.10}=2.58
\end{gathered}
$
We can apply this same logic to the half-life equation:
$
\begin{gathered}
\frac{A}{A_o}=\left(\frac{1}{2}\right)^{t / \tau} \\
\log A-\log A_o=\frac{t}{\tau} \log \left(\frac{1}{2}\right)
\end{gathered}
$
Sample problem:
Q: If you started with $64 \mathrm{~g}$ of ${ }^{131} \mathrm{I}$, how long would it take until there was only $5.75 \mathrm{~g}$ remaining? The half-life $(\tau)$ of ${ }^{131}$ is 8.07 days.
Answer/Explanation
A: We have $5.75 \mathrm{~g}$ remaining. However, $\frac{64}{5.75}=11.13$, which is not a power of two. This means we don’t have an integer number of half-lives, so we need to use logarithms:
$\begin{gathered}\frac{A}{A_o}=\left(\frac{1}{2}\right)^{t / \tau} \\ \log A-\log A_o=\frac{t}{\tau} \log \left(\frac{1}{2}\right) \\ \log 5.75-\log 64=\frac{t}{8.07} \log \left(\frac{1}{2}\right) \\ 0.7597-1.8062=\frac{t}{8.07}(-0.3010) \\ -1.0465=-0.03730 t \\ 28.1 \text { days }=t\end{gathered}$
Nuclear Fission & Fusion
Notes:
Fission
fission: splitting of the nucleus of an atom, usually by bombarding it with a highspeed neutron.
When atoms are split by bombardment with neutrons, they can divide in hundreds of ways. For example, when ${ }^{235} \mathrm{U}$ is hit by a neutron, it can split more than 200 ways. Three examples that have been observed are:
$
\begin{aligned}
& { }_0^1 n+{ }_{92}^{235} \mathrm{U} \rightarrow{ }_{37}^{90} \mathrm{Rb}+{ }_{55}^{144} \mathrm{Cs}+2{ }_0^1 n \\
& { }_0^1 n+{ }_{92}^{235} \mathrm{U} \rightarrow{ }_{35}^{87} \mathrm{Br}+{ }_{57}^{146} \mathrm{La}+3{ }_0^1 n \\
& { }_0^1 n+{ }_{92}^{235} \mathrm{U} \rightarrow{ }_{30}^{72} \mathrm{Br}+{ }_{62}^{160} \mathrm{Sm}+4{ }_0^1 n
\end{aligned}
$
Note that each of these bombardments produces more neutrons. A reaction that produces more fuel (in this case, neutrons) than it consumes will accelerate. This self-propagation is called a chain reaction.
Note also that the neutron/proton ratio of ${ }^{235} \mathrm{U}$ is about 1.5. The stable neutron/proton ratio of each of the products would be approximately 1.2. This means that almost all of the products of fission reactions have too many neutrons to be stable, which means they will themselves undergo $\beta$ – decay.
Nuclear Fission Reactors
In a nuclear reactor, the heat from a fission reaction is used to heat water. The radioactive hot water from the reactor (under pressure, so it can be heated well above $100^{\circ} \mathrm{C}$ without boiling) is used to boil clean (non-radioactive) water. The clean steam is used to turn a turbine, which generates electricity.
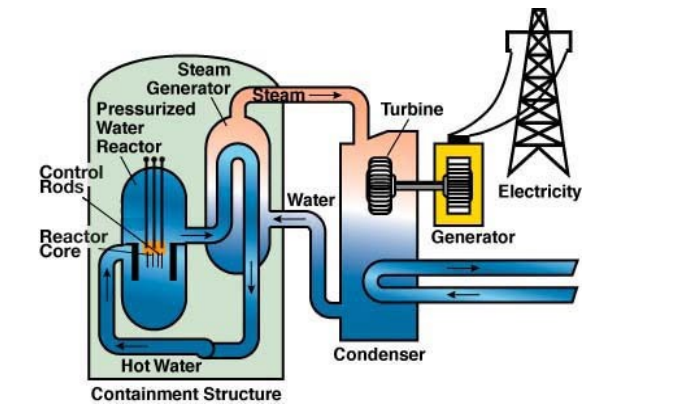
The inside of the reactor looks like this:
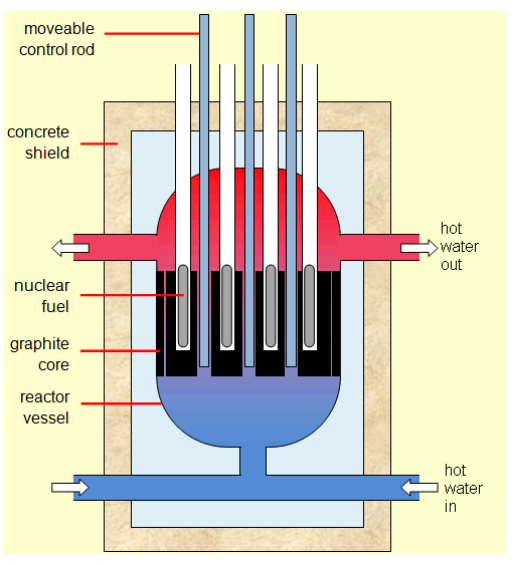
The fuel is the radioactive material (such as ${ }^{235} \mathrm{U}$ ) that is undergoing fission. The graphite in the core of the reactor is used to absorb some of the neutrons. The moveable control rods are adjusted so they can absorb some or all of the remaining neutrons as desired. If the control rods are all the way down, all of the neutrons are absorbed and no heating occurs. When the reactor is in operation, the control rods are raised just enough to make the reaction proceed at the desired rate.
Fusion
fusion: the joining together of the nuclei of two atoms, accomplished by colliding them at high speeds.
Nuclear fusion reactions occur naturally on stars (such as the sun), and are the source of the heat and energy that stars produce.
On the sun, fusion occurs between atoms of deuterium $\left({ }^2 \mathrm{H}\right)$ to produce helium:
$
{ }_1^2 \mathrm{H}+{ }_1^2 \mathrm{H} \rightarrow{ }_2^4 \mathrm{He}
$
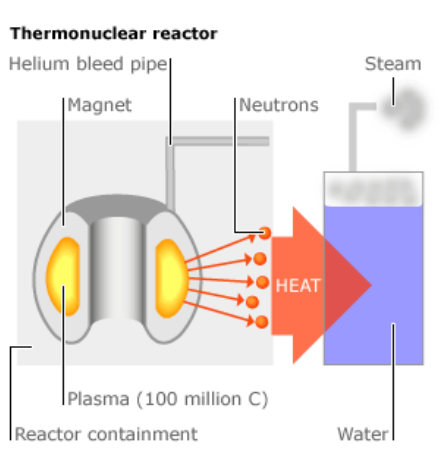
The major challenge in building nuclear fusion reactors is the high temperatures produced-on the order of $10^6-10^9 \mathrm{C}$. In a tokamak fusion reactor, the starting materials are heated until they become plasma-a sea of highly charged ions and electrons. The highly charged plasma is kept away from the sides by powerful electromagnets.
At the left is a schematic of the ITER tokamak reactor currently under construction in southern France.
MIT has a smaller tokamak reactor at its Plasma Science \& Fusion Center. The MIT reactor is able to conduct fusion reactions lasting for only a few seconds; if the reaction continued beyond this point, the current in the electromagnets that is necessary to generate the high magnetic fields required to confine the reaction would become hot enough to melt the copper wire and fuse the coils of the electromagnet together.
After each “burst” (short fusion reaction), the electromagnets in the MIT reactor need to be cooled in a liquid nitrogen bath $\left(-196^{\circ} \mathrm{C}\right)$ for fifteen minutes before the reactor is ready for the next burst.
Practical Uses for Nuclear Radiation
Notes:
While most people think of the dangers and destructive power of nuclear radiation, there are a lot of other uses of radioactive materials:
Power Plants: nuclear reactors can generate electricity in a manner that does not produce $\mathrm{CO}_2$ and other greenhouse gases.
Cancer Therapy: nuclear radiation can be focused in order to kill cancer cells in patients with certain forms of cancer. Radioprotective drugs are now available that can help shield non-cancerous cells from the high-energy gamma rays.
Radioactive Tracers: chemicals made with radioactive isotopes can be easily detected in complex mixtures or even in humans. This enables doctors to give a patient a chemical with a small amount of radioactive material and track the progress of the material through the body and determine where it ends up. It also enables biologists to grow bacteria with radioactive isotopes and follow where those isotopes end up in subsequent experiments.
Irradiation of Food: food can be exposed to high-energy gamma rays in order to kill germs. These gamma rays kill all of the bacteria in the food, but do not make the food itself radioactive. (Gamma rays cannot build up inside a substance.) This provides a way to create food that will not spoil for months on a shelf in a store. There is a lot of irrational fear of irradiated food in the United States, but irradiation is commonly used in Europe. For example, irradiated milk will keep for months on a shelf at room temperature without spoiling.
Carbon Dating: Because ${ }^{14} \mathrm{C}$ is a long-lived isotope (with a half-life of 5700 years), the amount of ${ }^{14} \mathrm{C}$ in archeological samples can give an accurate estimate of their age. One famous use of carbon dating was its use to prove that the Shroud of Turin (the supposed burial shroud of Jesus Christ) was fake, because it was actually made between 1260 C.E. and 1390 C.E.
Smoke Detectors: In a smoke detector, ${ }^{241}$ Am emits positively-charged alpha particles, which are directed towards a metal plate. This steady flow of positive charges completes an electrical circuit. If there is a fire, smoke particles neutralize positive charges. This makes the flow of charges through the electrical circuit stop, which is used to trigger the alarm.