Topics covered in this chapter:
Some Devices that Produce, Use or Store Charge
capacitor: a device that stores electric charge.
battery: a device that uses chemical reactions to produce an electric current.
generator: a device that converts mechanical energy (motion) into an electric current.
motor: a device that converts an electric current into mechanical energy.
Conductors vs. Insulators
conductor: a material that allows charges to move freely through it. Examples of conductors include metals and liquids with positive and negative ions dissolved in them (such as salt water). When charges are transferred to a conductor, the charges distribute themselves evenly throughout the substance.
insulator: a material that does not allow charges to move freely through it. Examples of insulators include nonmetals and most pure chemical compounds (such as glass or plastic). When charges are transferred to an insulator, they cannot move, and remain where they are placed.
Behavior of Charged Particles
- Like charges repel. A pair of the same type of charge (two positive charges or two negative charges) exert a force that pushes the charges away from each other.
- Opposite charges attract. A pair of opposite types of charge (a positive charge and a negative charge) exert a force that pulls the charges toward each other.
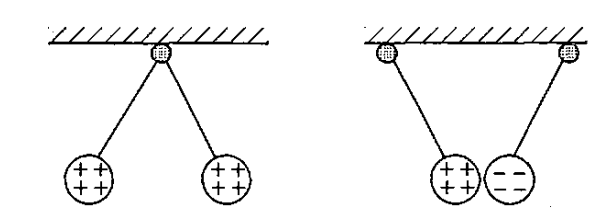
- Charge is conserved. Electric charges cannot be created or destroyed, but can be transferred from one location or medium to another. (This is analogous to the laws of conservation of mass and energy.)
Note that if you were to place a charge (either positive or negative) on a solid metal sphere, the charges would repel, and the result would be that the charges would be spread equally over the outside surface, but not inside the sphere.
Charging by Induction
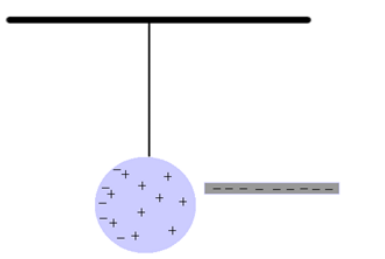
induction: when an electrical charge on one object causes a charge in a second object.
When a charged rod is brought near a neutral object, the charge on the rod attracts opposite charges and repels like charges that are near it. The diagram to the right shows a negatively-charged rod repelling negative charges.
If the negatively-charged rod were touched to the sphere, some of the charges from the rod would be transferred to the sphere at the point of contact. This would cause the sphere to have an overall negative charge.
A procedure for inducing charges in a pair of metal spheres is shown below:
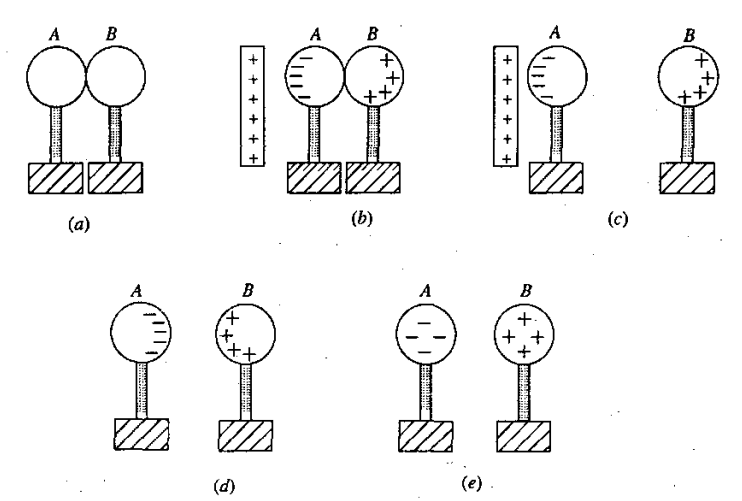
(a) Metal spheres A and B are brought into contact.
(b) A positively charged object is placed near (but not in contact with) sphere A. This induces a negative charge in sphere A, which in turn induces a positive charge in sphere B.
(c) Sphere B (which is now positively charged) is moved away.
(d) The positively charged object is removed.
(e) The charges distribute themselves throughout the metal spheres.
Electric Charge
Notes:
charge:
1. A physical property of matter which causes it to experience a force when near other electrically charged matter. (Sometimes called “electric charge”.) Measured in coulombs (C).
2. A single microscopic object (such as a proton or electron) that carries an electric charge. (Sometimes called a “point charge.) Denoted by the variable $q$.
3. The total amount of electric charge on a macroscopic object (caused by an accumulation of microscopic charged objects). Denoted by the variable $Q$.
4. (verb) To cause an object to acquire an electric charge.
positive charge: the charge of a proton. Originally defined as the charge left on a piece of glass when rubbed with silk. The glass becomes positively charged because the silk pulls electrons off the glass.
negative charge: the charge of an electron. Originally defined as the charge left on a piece of amber (or rubber) when rubbed with fur (or wool). The amber becomes negatively charged because the amber pulls the electrons off the fur.
static electricity: stationary electric charge, such as the charge left on silk or amber in the above definitions.
elementary charge: the magnitude (amount) of charge on one proton or one electron. One elementary charge equals $1.60 \times 10^{-19} \mathrm{C}$. Because ordinary matter is made of protons and electrons, the amount of charge carried by any object must be an integer multiple of the elementary charge.
Note however, that the quarks that protons and neutrons are made of carry fractional charges; up-type quarks carry a charge of $+2 / 3$ of an elementary charge, and down-type quarks carry a charge of $-1 / 3$ of an elementary charge. A proton is made of two up quarks and one down quark and carries a charge of +1 elementary charge. A neutron is made of one up quark and two down quarks and carries no charge.

electric current (sometimes called electricity): the movement of electrons through a medium (substance) from one location to another. Note, however, that electric current is defined as the direction a positively charged particle would move. Thus electric current “flows” in the opposite direction from the actual electrons.
Charge Density
The amount of electric charge on a surface is called the charge density. As with density (in the mass/volume sense), the variable used is usually the Greek letter rho with a subscript $q$ indicating charge $\left(\rho_q\right)$. Charge density can be expressed in terms of length, area, or volume, which means, the units for charge density can be $\frac{\mathrm{c}}{\mathrm{m}}, \frac{\mathrm{c}}{\mathrm{m}^2}$, or $\frac{\mathrm{c}}{\mathrm{m}^3}$
Grounding
For the purposes of our use of electric charges, the ground (Earth) is effectively an endless supply of both positive and negative charges. Under normal circumstances, if a charged object is touched to the ground, electrons will move to neutralize the charge, either by flowing from the object to the ground or from the ground to the object.
Grounding a charged object or circuit means neutralizing the electrical charge on an object or portion of the circuit. The charge of any object that is connected to ground is zero, by definition.
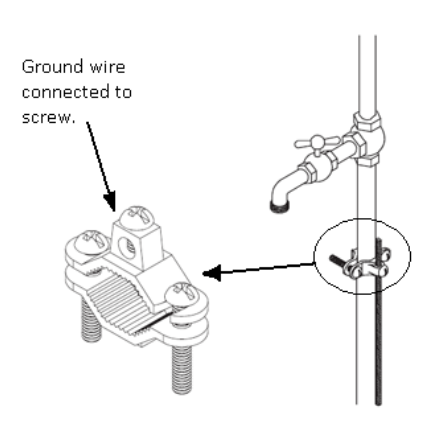
In buildings, the metal pipes that bring water into the building are often used to ground the electrical circuits. The metal pipe is a good conductor of electricity, and carries the unwanted charge out of the building and into the ground outside.
Coulomb’s Law
Notes:
Electric charge is measured in Coulombs (abbreviation ” $C$ “). One Coulomb is the amount of electric charge transferred by a current of 1 ampere for a duration of 1 second.
$+1 C$ is the charge of $6.2415 \times 10^{18}$ protons.
$-1 C$ is the charge of $6.2415 \times 10^{18}$ electrons.
A single proton or electron therefore has a charge of $\pm 1.6022 \times 10^{-19} \mathrm{C}$. This amount of charge is called the elementary charge, because it is the charge of one elementary particle.
An object can only have an integer multiple of this amount of charge, because it is impossible ${ }^*$ to have a charge that is a fraction of a proton or electron.
Because charged particles attract or repel each other, that attraction or repulsion must be a force, which can be measured and quantified. The force is directly proportional to the strengths of the charges, and inversely proportional to the square of the distance. The formula is:
$
F_e=\frac{k q_1 q_2}{r^2}
$
where:
$F_e=$ electrostatic force of repulsion between electric charges. A positive value of $F_e$ denotes that the charges are repelling (pushing away from) each other; a negative value of $F_e$ denotes that the charges are attracting (pulling towards) each other.
$k=$ electrostatic constant $=8.9876 \times 10^9 \frac{\mathrm{N} \cdot \mathrm{m}^2}{\mathrm{c}^2}$, which we usually approximate as $9.0 \times 10^9 \frac{\mathrm{N} \cdot \mathrm{m}^2}{\mathrm{c}^2}$
$q_1, q_2=$ the charges on objects \#1 and $\# 2$ respectively
$r=$ distance (radius, because it goes outward in every direction) between the centers of the two charges
This formula is Coulomb’s Law, named for its discoverer, the French physicist Charles-Augustin de Coulomb.
” This is true for macroscopic objects. Certain quarks, which are the particles that protons and neutrons are made of, have charges of $1 / 3$ or $2 / 3$ of an elementary charge.
Sample problems:
Q: Find the force of electrostatic attraction between the proton and electron in a hydrogen atom if the radius of the atom is $37.1 \mathrm{pm}$
Answer/Explanation
A: The charge of a single proton is $1.60 \times 10^{-19} \mathrm{C}$, and the charge of a single electron is $-1.60 \times 10^{-19} \mathrm{C}$.
$
\begin{aligned}
& 37.1 \mathrm{pm}=3.71 \times 10^{-11} \mathrm{~m} \\
& F_e=\frac{k q_1 q_2}{r^2} \\
& F_e=\frac{\left(8.99 \times 10^9\right)\left(1.60 \times 10^{-19}\right)\left(-1.60 \times 10^{-19}\right)}{\left(3.71 \times 10^{-11}\right)^2} \\
& F_e=-1.67 \times 10^{-7} \mathrm{~N}
\end{aligned}
$
The value of the force is negative, which signifies that the force is attractive. However, rather than memorize whether a positive or negative indicates attraction or repulsion, it’s easier to reason that the charges are opposite, so the objects attract. Never memorize what you can understand!
Electric Fields
Notes:
force field: a region in which an object experiences a force because of some intrinsic property of the object that enables the force to act on it. Force fields are vectors, which means they have both a magnitude and a direction.
electric field $(\vec{E})$ : an electrically charged region (force field) that exerts a force on any charged particle within the region.
An electric field applies a force to an object based on its electrical charge. $\overrightarrow{\boldsymbol{F}}_e=q \overrightarrow{\boldsymbol{E}}$, where $\overrightarrow{\boldsymbol{E}}$ represents the magnitude and direction of the electric field.
Because gravity is a familiar concept, it is useful to use gravitational fields as a way to explain force fields, and thus electric fields.
Recall that a gravitational field applies a force to an object based on its mass. $\overrightarrow{\boldsymbol{F}}_g=m \overrightarrow{\boldsymbol{g}}$, where $\overrightarrow{\boldsymbol{g}}$ represents the magnitude and direction of the gravitational field.
Just as a gravitational field applies a force to an object that has mass, an electric field applies a force to an object that has charge:
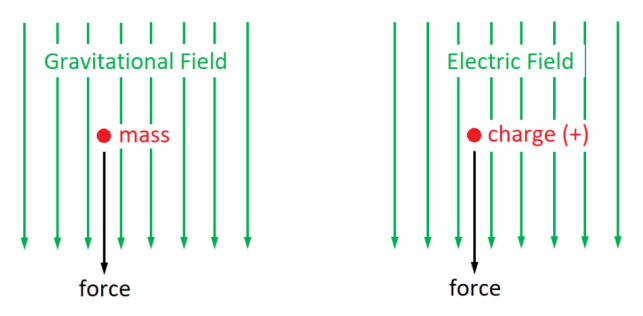
A key difference between the two situations is that there are two kinds of charges-positive and negative-whereas there is only one kind of mass.
The force on an object with mass is always in the direction of the gravitational field. However, the direction of the force on an object with charge depends on whether the charge is positive or negative. The force on an object with positive charge is in the same direction as the electric field; the force on an object with negative charge is always in the opposite direction from the electric field.
For any force field, the amount of force is the amount of the quantity that the field acts on times the strength of the field:
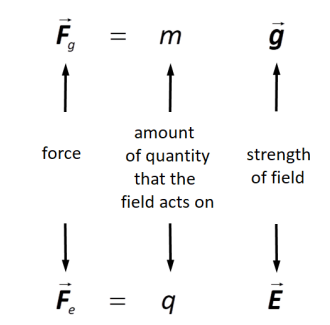
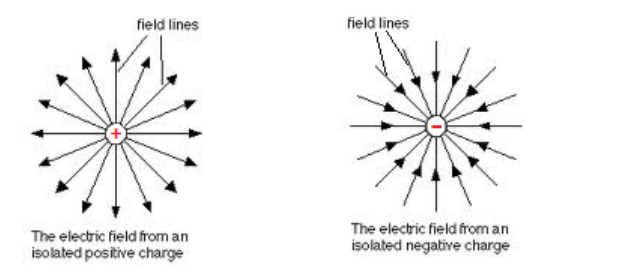
field lines: lines with arrows that show the direction of an electric field. In the above diagrams, the arrows are the field lines.
Field lines are lines that show the directions of force on an object. As described above, for an electric field, the object is assumed to be a positively-charged particle. This means that the direction of the electric field is from positive to negative. This means that field lines go outward in all directions from a positively-charged particle, and inward from all directions toward a negativelycharged particle.
This means that a positively-charged particle (such as a proton) would move in the direction of the arrows, and a negatively charged particle (such as an electron) would move in the opposite direction.
The simplest electric field is the region around a single charged particle:
If a positive and a negative charge are near each other, the field lines go from the positive charge toward the negative charge:
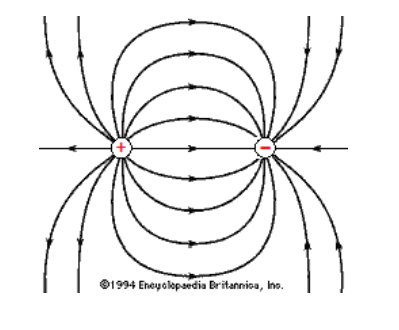
(Note that even though this is a two-dimensional drawing, the field itself is threedimensional. Some field lines come out of the paper from the positive charge and go into the paper toward the negative charge, and some go behind the paper from the positive charge and come back into the paper from behind toward the negative charge.)
In the case of two charged plates (flat surfaces), the field lines would look like the following:

Electric Field Strength
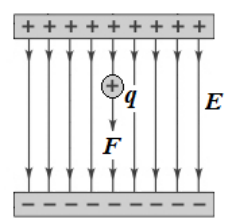
We can measure the strength of an electric field by placing a particle with a positive charge $(q)$ in the field and measuring the force $(\overrightarrow{\boldsymbol{F}})$ on the particle.
Coulomb’s Law tells us that the force on the charge is due to the charges from the electric field:
$
F_e=\frac{k q_1 q_2}{r^2}
$
If the plates have equal charge densities, the repulsive force from the like-charged plate decreases as the particle moves away from it, but the attractive force from the oppositely-charged plate increases by the same amount as the particle moves toward it.
This means that if the positive and negative charges on the two surfaces that make the electric field have equal charge densities, the force is the same everywhere in between the two surfaces. The force on the particle is related only to the strength of the electric field and the charge of the particle.
This results in the equation that defines the electric field $(\vec{E})$ as the force between the electric field and our particle, divided by the charge of our particle:
$
\overrightarrow{\boldsymbol{E}}=\frac{\overrightarrow{\boldsymbol{F}}}{q} \quad \text { or } \quad \overrightarrow{\boldsymbol{F}}=q \overrightarrow{\boldsymbol{E}}
$
Work Done on a Charge by an Electric Field
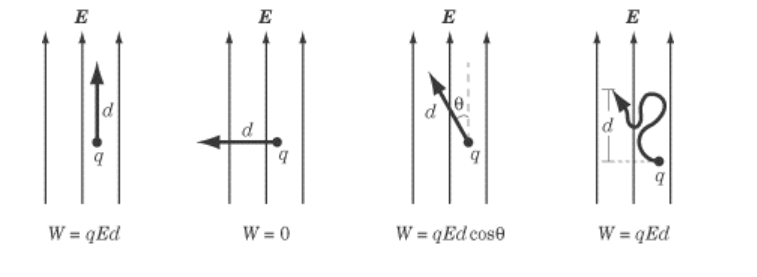
Recall that work is the dot product of force and displacement:
$
W=\overrightarrow{\boldsymbol{F}} \cdot \overrightarrow{\boldsymbol{d}}=F d \cos \theta
$
Because $W=\Delta U$, the potential energy of an electric field is the work that it is able to do. This means:
$
U_e=\overrightarrow{\boldsymbol{F}}_e \cdot \overrightarrow{\boldsymbol{d}}=\frac{k q_1 q_2}{r^2} \cdot r=\frac{k q_1 q_2}{r}
$
Because $\overrightarrow{\boldsymbol{F}}=q \overrightarrow{\boldsymbol{E}}$, we can substitute:
$
W=\overrightarrow{\boldsymbol{F}} \cdot \overrightarrow{\boldsymbol{d}}=q \overrightarrow{\boldsymbol{E}} \cdot \overrightarrow{\boldsymbol{d}}=q E d \cos \theta
$
Electric Potential
Recall from the work-energy theorem that work equals a change in energy. Because an electric field can do work on a charged particle, an electric field must therefore apply energy to the particle.
electric potential $(V)$ : the electric potential energy of a charged particle in an electric field.
Electric potential is measured in volts $(\mathrm{V})$.
$
1 \mathrm{~V} \equiv 1 \frac{\mathrm{N} \cdot \mathrm{m}}{\mathrm{C}} \equiv 1 \frac{\mathrm{J}}{\mathrm{C}}
$
Electric potential is analogous to gravitational potential energy. In a gravitational field, a particle has gravitational potential energy because gravity can make it move. In an electric field, a particle has electric potential (energy) because the electric field can make it move.
For example, if we had a $1 \mathrm{~kg}$ mass and we placed it at a height of $4 \mathrm{~m}$ above the ground, its gravitational potential would be $U_g=m g h=(1)(10)(4)=40 \mathrm{~J}$.
Similarly, if we put an object with a charge of $1 \mathrm{C}$ at a location that has an electric potential of $40 \mathrm{~V}$, that object would have $40 \mathrm{~J}$ of potential energy due to the electric field.

Sample Problem:
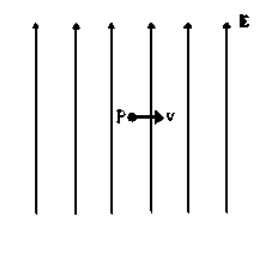
Q: A proton has a velocity of $1 \times 10^5 \frac{\mathrm{m}}{\mathrm{s}}$ when it is at point $P$ in a uniform electric field that has an intensity of $1 \times 10^4 \frac{\mathrm{N}}{\mathrm{C}}$. Calculate the force (magnitude and direction) on the proton and sketch its path.
Answer/Explanation
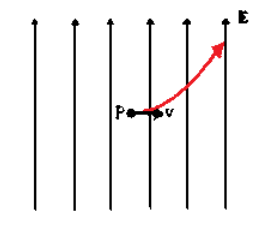
A: The force on the proton is given by:
$
\overrightarrow{\boldsymbol{F}}_e=q \overrightarrow{\boldsymbol{E}}=\left(1.6 \times 10^{-19}\right)\left(1 \times 10^4\right)=1.6 \times 10^{-15} \mathrm{~N}
$
The direction of the force is the same direction as the electric field, which in this problem is upwards.
An upward force causes acceleration upwards. Because the proton starts with a velocity only to the right, upward acceleration means that its velocity will have a continuously increasing vertical component.
Electric Field Vectors
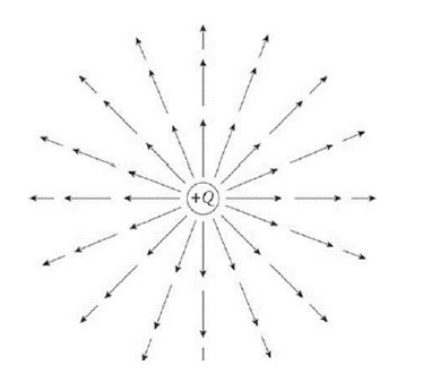
electric field vector: an arrow representing the strength and direction of an electric field at a point represented on a map.
A map of an electric field can be drawn using field vectors instead of field lines. Electric field vectors are preferred, because in addition to showing the direction of the electric field at a given
location, they also show the relative strength. For example, this diagram shows the electric field around a positive charge. Notice that:
• The vectors point in the direction of the electric field (from positive to negative).
• The vectors are longer where the electric field is stronger and shorter where the electric field is weaker.
The electric field vectors around a pair of point charges, one positive and one negative, would look like the following:

If the point charges were not shown, you could use a field vector diagram to determine their locations:
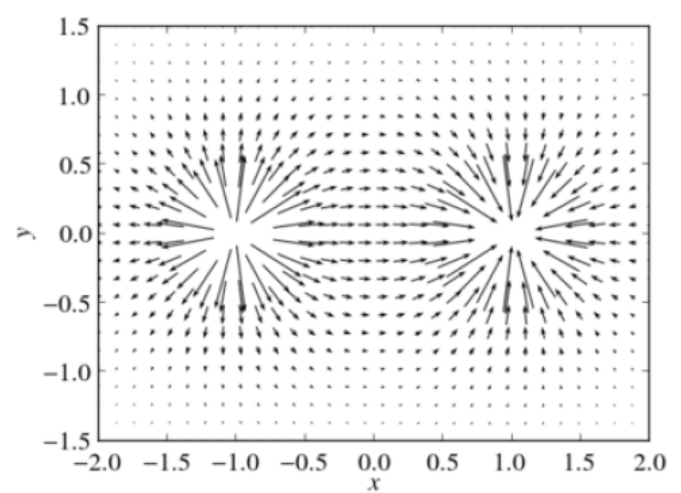
In the above example, there must be a positive point charge at coördinates (−1.0, 0) and a negative point charge at coördinates (+1.0, 0)
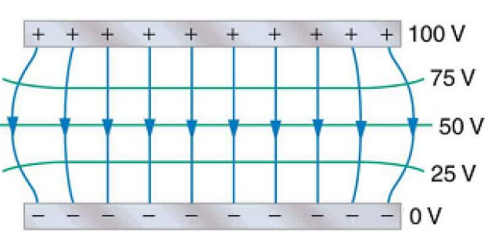
Equipotential Lines & Maps
Notes:
isoline or equipotential line: a line on a map that connects regions of equal electric potential.
Isolines are the equivalent of elevation lines on a contour map. Below is a contour map (top) and side view of the same landscape (bottom):
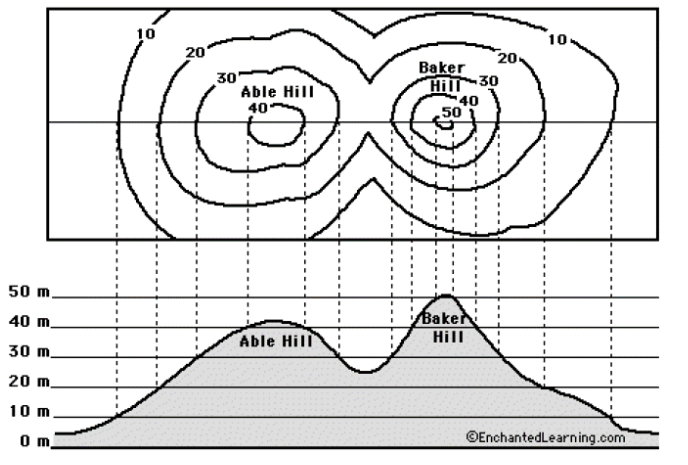
The contour map (top) is a view from above. Each contour line connects points that have the same elevation.
Similar to contour lines, equipotential lines connect regions of the same electric potential.
For example, the electric field direction is away from a positive point charge. The electric field strength decreases as you get farther away from the point charge. The equipotential lines (isolines) are therefore circles around the point charge; circles closer to the charge have higher electric potential, and circles farther away have lower electric potential.
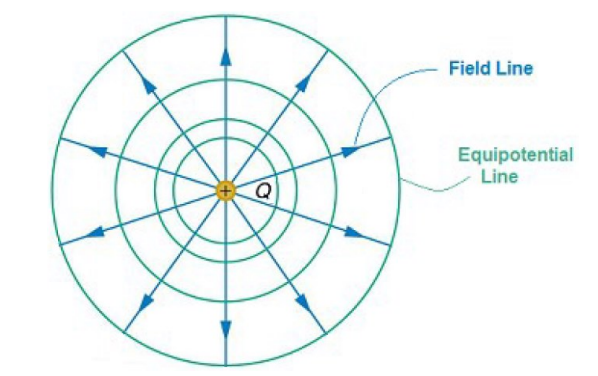
Notice that the equipotential lines are perpendicular to the field lines. As you travel along a field line, the electric potential becomes continuously less positive or more negative. The equipotential lines are the mileposts that show what the electric potential is at that point.
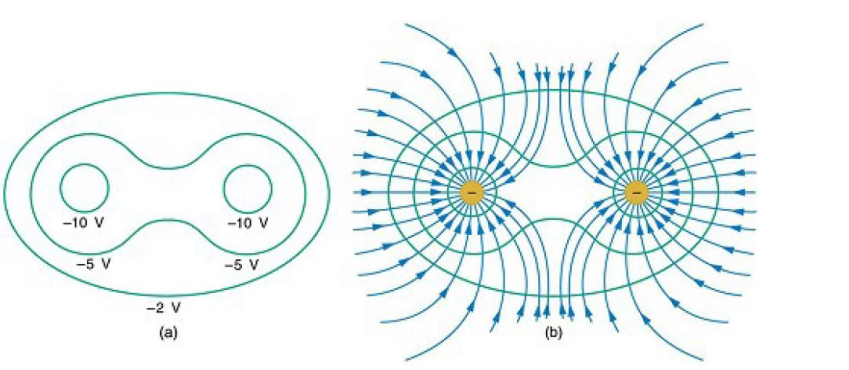
If you were given only the equipotential lines, you could determine what the resulting field lines looked like. For example, in the illustration below, if you were given the isolines in diagram (a), you would infer that the regions inside each of the smaller isolines must be negative point charges, and that the electric field becomes more and more negative as you approach those points.
Because the electric field lines go from positive to negative, the field lines must therefore point into the points, resulting in diagram (b). Notice again that the field lines are always perpendicular to the isolines.
The electric field lines and isolines for the region between two parallel plates would look like the following: