Topics covered in this chapter:
Notes:
pressure: the exertion of force upon a surface by an object, fluid, etc. that is in contact with it.
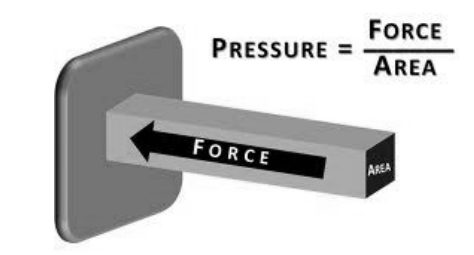
Mathematically, pressure is defined as force divided by area:
$
P=\frac{F}{A}
$
The S.I. unit for pressure is the pascal (Pa).
$
1 \mathrm{~Pa} \equiv 1 \frac{\mathrm{N}}{\mathrm{m}^2} \equiv 1 \frac{\mathrm{kg}}{\mathrm{ms}^2}
$
(Note that Pa is a two-letter symbol.)
Some other common pressure units are:
- bar: 1 bar $\equiv 100000 \mathrm{~Pa}$
- pound per square inch (psi)
- atmosphere (atm): the average atmospheric pressure on Earth at sea level.
$1 \mathrm{~atm} \equiv 101325 \mathrm{~Pa} \equiv 1.01325 \mathrm{bar}=14.696 \mathrm{psi}$
In this course, we will use the approximation that $1 \mathrm{~atm} \approx 1$ bar, meaning that standard atmospheric pressure is $1 \mathrm{bar} \equiv 100000 \mathrm{~Pa}$.
Air pressure can be described relative to a total vacuum (absolute pressure), but is more commonly described relative to atmospheric pressure (gauge pressure):
- absolute pressure: the total pressure on a surface. An absolute pressure of zero means there is zero force on the surface.
- gauge pressure: the difference between the pressure on a surface and atmospheric pressure. A gauge pressure of zero means the same as atmospheric pressure. The pressure in car tires is measured as gauge pressure. For example, a tire pressure of $30 \mathrm{psi}$ ( 30 pounds per square inch, or $30 \frac{\mathrm{lb} .}{\mathrm{in.}^2}$ ) would mean that the air inside the tires is pushing against the air outside the tires with a pressure of 30 psi.
A flat tire would have a gauge pressure of zero and an absolute pressure of about 1 bar.
Sample Problem
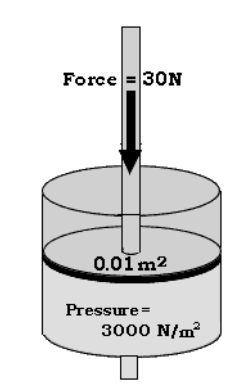
Q: What is the pressure caused by a force of $25 \mathrm{~N}$ acting on a piston with an area of $0.05 \mathrm{~m}^2$ ?
Answer/Explanation
A: $\quad P=\frac{F}{A}=\frac{25 \mathrm{~N}}{0.05 \mathrm{~m}^2}=500 \mathrmIntroduction: Fluids & Pressure{~Pa}$
Hydraulic Pressure
Notes:
Pascal’s Principle, which was discovered by the French mathematician Blaise Pascal, states that any pressure applied to a fluid is transmitted uniformly throughout the fluid.
Because $P=\frac{F}{A}$, if the pressure is the same everywhere in the fluid, then $\frac{F}{A}$ must be the same everywhere in the fluid.
If you have two pistons whose cylinders are connected, the pressure is the same throughout the fluid, which means the force on each piston is proportional to its own area. Thus:
$
\mathrm{P}_1=\mathrm{P}_2 \quad \text { which means } \quad \frac{F_1}{A_1}=\frac{F_2}{A_2}
$
This principle is called “hydraulics.” If you have a lift that has two pistons, one that is 100 times larger than the other, the larger one can supply 100 times as much force.
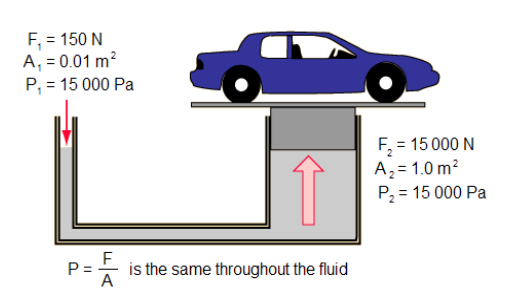
This seems like we’re getting something for nothing-we’re lifting a car by applying only $150 \mathrm{~N}$ of force (approximately $35 \mathrm{lbs}$.). However, conservation of energy tells us that the work done by $F_1$ must equal the work done by $F_2$, which means $F_1$ must act over a considerably larger distance than $F_2$. In order to lift the car on the right $10 \mathrm{~cm}$ (about 4 in.), you would have to press the plunger on the left $10 \mathrm{~m}$.
You could also figure this out by realizing that the volume of fluid transferred on both sides must be the same and multiplying the area by the distance.
This is how hydraulic brakes work in cars. When you step on the brake pedal, the hydraulic pressure is transmitted to the master cylinder and then to the slave cylinders. The master cylinder is much smaller in diameter than the slave cylinders, which means the force applied to the brake pads is considerably greater than the force from your foot.
Sample Problem
Q: In a hydraulic system, a force of $25 \mathrm{~N}$ will be applied to a piston with an area of $0.50 \mathrm{~m}^2$. If the force needs to lift a weight of $500 . \mathrm{N}$, what must be the area of the piston supporting the 500 . $\mathrm{N}$ weight? $25 A_2=(500)(0.50)$
Answer/Explanation
A: $\frac{F_1}{A_1}=\frac{F_2}{A_2}$ $\frac{25}{0.50}=\frac{500}{A_2}$ $25 A_2=250$ $A_2=10 \mathrm{~m}^2$
Hydrostatic Pressure
Notes:
hydrostatic pressure: the pressure caused by the weight of a column of fluid
The force of gravity pulling down on the particles in a fluid creates pressure. The more fluid there is above a point, the higher the pressure at that point.
The atmospheric pressure that we measure at the surface of the Earth is caused by the air above us, all the way to the highest point in the atmosphere, as shown in the picture at right:
Assuming the density of the fluid is constant, the pressure in a column of fluid is caused by the weight (force of gravity) acting on an area. Because the force of gravity is $m g$ (where $g=10 \frac{\mathrm{N}}{\mathrm{kg}}$ ), this means:
$
P_H=\frac{F_g}{A}=\frac{m g}{A}
$
where: $
\begin{aligned}
P_H & =\text { hydrostatic pressure } \\
g & =\text { strength of gravitational field }\left(10 \frac{\mathrm{N}}{\mathrm{kg}} \text { on Earth }\right)
\end{aligned}
$
$A=$ area of the surface the fluid is pushing on
We can cleverly multiply and divide our equation by volume:
$
P_H=\frac{m g}{A}=\frac{m g \cdot V}{A \cdot V}=\frac{m}{V} \cdot \frac{g V}{A}
$
Then, we need to recognize that (1) density $\left(\rho^*\right)$ is mass divided by volume, and (2) the volume of a region is the area of its base times the height $(h)$. Thus the equation becomes:
$
\begin{aligned}
& P_H=\rho \cdot \frac{g V}{A}=\rho \cdot \frac{g A h}{A} \\
& P_H=\rho g h
\end{aligned}
$
Finally, if there is an external pressure, $P_o$, above the fluid, we have to add it to the hydrostatic pressure from the fluid itself, which gives us the familiar form of the equation:
$
P=P_o+P_H=P_o+\rho g h
$
where:
$
\begin{aligned}
& P_H=\text { hydrostatic pressure } \\
& P_o=\text { pressure above the fluid (if relevant) } \\
& \rho=\text { density of the fluid (this is the Greek letter “rho”) } \\
& g=\text { acceleration due to gravity }\left(10 \frac{\mathrm{m}}{\mathrm{s}^2}\right. \text { on Earth) } \\
& h=\text { height of the fluid above the point of interest }
\end{aligned}
$
Sample Problem
Q: What is the water pressure in the ocean at a depth of $25 \mathrm{~m}$ ? The density of sea water is $1025 \frac{\mathrm{kg}}{\mathrm{m}^3}$.
Answer/Explanation
A: $P_H=\rho g h=(1025)(10)(25)=256250 \mathrm{~Pa}=2.56 \mathrm{bar}$
Buoyancy
Notes:
displace: to push out of the way
buoyancy: a net upward force caused by the differences in hydrostatic pressure at different levels within a fluid:
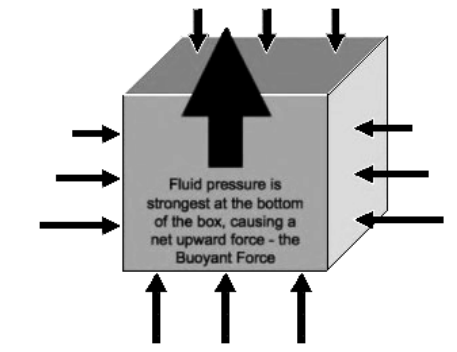
The hydrostatic pressure is stronger at the bottom of the object than at the top, which causes a net upward force on the object.
When an object displaces a fluid:
1. The volume of the fluid displaced equals the volume of the submerged part of the object: $V_{\text {fluid displaced }}=V_{\text {submerged part of object }}$
2. The weight of the fluid displaced equals the buoyant force $\left(F_B\right)$.
3. The net force on the object, if any, is the difference between its weight and the buoyant force: $F_{\text {net }}=F_g-F_B$
The buoyant force is caused by the difference in hydrostatic pressure from the bottom of the object to the top, i.e., $F_B=P A_d$. However, the hydrostatic pressure is a function of the depth and the area is a function of the shape of the object. By manipulating the equations and recognizing that area times height equals volume, we get the equation for the buoyant force:
$
F_B=\rho V_d g
$
Where:
$
\begin{aligned}
& F_B=\text { buoyant force }(\mathrm{N}) \\
& \rho=\text { density of fluid }\left(\frac{\mathrm{kg}}{\mathrm{m}^3}\right) ; \text { fresh water }=1000 \frac{\mathrm{kg}}{\mathrm{m}^3} \\
& V_d=\text { volume of fluid displaced }\left(\mathrm{m}^3\right) \\
& g=\text { strength of gravitational field }\left(g=10 \frac{\mathrm{N}}{\mathrm{kg}}\right)
\end{aligned}
$
For those who want a calculus-based explanation, the hydrostatic force over the surface of the object is given by combining the hydrostatic equation:
$
P_H=\int \rho g d h
$
with the equation for pressure, rearranged to solve for force:
$
\mathrm{F}=\mathrm{PA}
$
We recognize that because the area varies with depth, this results in a double surface integral over the area of the object $(d A)$ and the height $(d h)$ :![]()
Conveniently, ![]() is simply the volume of the part of the object that is submerged, which is equal to the volume of fluid displaced.
is simply the volume of the part of the object that is submerged, which is equal to the volume of fluid displaced.
Therefore: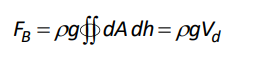
Detailed Explanation
If the object floats, there is no net force, which means the weight of the object is equal to the buoyant force. This means:
$
\begin{aligned}
F_g & =F_B \\
m g & =\rho v_d g
\end{aligned}
$
Cancelling $g$ from both sides gives $m=\rho V_d$, which can be rearranged to give the equation for density:
$
\rho=\frac{m}{V_d}
$
Therefore:
- If the object floats, the mass of the object equals the mass of the fluid displaced
- The volume of the fluid displaced equals the volume of the object that is submerged.
If the object sinks, the weight of the object is greater than the buoyant force. This means:
$
\begin{aligned}
& F_B=\rho V_d g \\
& F_g=m g
\end{aligned}
$
Therefore:
- The weight of the submerged object is $F_{n e t}=F_g-F_B$
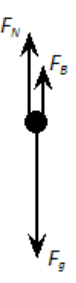
Note that if the object is resting on the bottom of the container, the net force must be zero, which means the normal force and the buoyant force combine to supply the total upward force. I.e., for an object resting on the bottom:
$
F_{n e t}=0=F_g-\left(F_B+F_N\right)
$
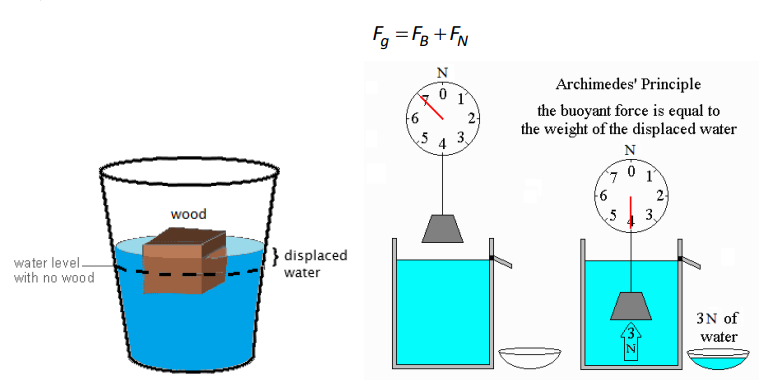
This concept is known as Archimedes’ Principle, named for the ancient Greek scientist who discovered it.
The buoyant force can be calculated from the following equation:
$
F_B=m_d g=\rho V_d g
$
Where:
$
\begin{aligned}
F_B & =\text { buoyant force } \\
m_d & =\text { mass of fluid displaced by the object } \\
g & =\text { strength of gravitational field }\left(10 \frac{\mathrm{N}}{\mathrm{kg}}\right. \text { on Earth) } \\
\rho & =\text { density of the fluid applying the buoyant force (e.g., water, air) } \\
V_d & =\text { volume of fluid displaced by the object }
\end{aligned}
$
Sample Problems:
Q: A cruise ship displaces 35000 tonnes of water when it is floating.
(1 tonne $=1000 \mathrm{~kg}$ ) If sea water has a density of $1025 \frac{\mathrm{kg}}{\mathrm{m}^3}$, what volume of water does the ship displace? What is the buoyant force on the ship?
Answer/Explanation
$
A: \begin{aligned}
\rho & =\frac{m}{V_d} \\
1025 & =\frac{(35000)(1000)}{V_d} \\
V_d & =34146 \mathrm{~m}^3 \\
F_B & =\rho V_d=(1025)(34146)(10)=3.5 \times 10^8 \mathrm{~N}
\end{aligned}
$
Q: Consider the following cartoon:

Given the following assumptions:
The balloons are standard $11^{\prime \prime}$ balloons, meaning that they have a diameter of 11 inches $(28 \mathrm{~cm})$, which equals a radius of $14 \mathrm{~cm}=0.14 \mathrm{~m}$.
- The temperature is $20^{\circ} \mathrm{C}$. At this temperature, air has a density of $1.200 \frac{\mathrm{kg}}{\mathrm{m}^3}$, and helium has a density of $0.166 \frac{\mathrm{kg}}{\mathrm{m}^3}$.
- Pasquale (the child) is probably about four years old. The average mass a four-year-old boy is about $16 \mathrm{~kg}$.
- The mass of an empty balloon plus string is $2.37 \mathrm{~g}=0.00237 \mathrm{~kg}$
How many balloons would it actually take to lift Pasquale?Answer/Explanation
A: In order to lift Pasquale, $F_B=F_{\mathrm{g}}$.
$
\begin{aligned}
& F_g=m g=(16)(10)=160 \mathrm{~N} \\
& F_B=\rho_{\text {air }} V_d g=(1.2) V_d(10)
\end{aligned}
$
Because $F_{\mathrm{B}}=F_{\mathrm{g}}$, this means:
$
\begin{aligned}
160 & =12 V_d \\
V_d & =13 . \overline{3} \mathrm{~m}^3
\end{aligned}
$
Assuming spherical balloons, the volume of one balloon is:
$
V=\frac{4}{3} \pi r^3=\left(\frac{4}{3}\right)(3.14)(0.14)^3=0.0115 \mathrm{~m}^3
$
Therefore, we need $\frac{13 . \overline{3}}{0.0115}=1160$ balloons to lift Pasquale.However, the problem with this answer is that it doesn’t account for the mass of the helium, the balloons and the strings.
Each balloon contains $0.0115 \mathrm{~m}^3 \times 0.166 \frac{\mathrm{kg}}{\mathrm{m}^3}=0.00191 \mathrm{~kg}$ of helium.
Each empty balloon (including the string) has a mass of $2.37 \mathrm{~g}=0.00237 \mathrm{~kg}$.
The total mass of each balloon full of helium is
$1.91 \mathrm{~g}+2.37 \mathrm{~g}=4.28 \mathrm{~g}=0.00428 \mathrm{~kg}$.
This means if we have $n$ balloons, the total mass of Pasquale plus the balloons is $16+0.00428 n$ kilograms. The total weight (in newtons) of Pasquale plus the balloons is therefore this number times 10 , which equals $160+0.0428 n$.
The buoyant force of one balloon is:
$
F_B=\rho_{\text {air }} V_d g=(1.2)(0.0115)(10)=0.138 \mathrm{~N}
$
Therefore, the buoyant force of $n$ balloons is $0.138 n$ newtons.
For Pasquale to be able to float, $F_{\mathrm{B}}=F_{\mathrm{g}}$, which means
$
\begin{aligned}
& 0.138 n=0.0428 n+160 \\
& 0.0952 n=160 \\
& n=1680 \text { balloons }
\end{aligned}
$
Fluid Motion & Bernoulli’s Law
Notes:
flow: the net movement of a fluid
velocity of a fluid: the average velocity of a particle of fluid as the fluid flows past a reference point. (unit $=\frac{m}{s}$ )
volumetric flow rate: the volume of a fluid that passes through a section of pipe in a given amount of time. (unit $=\frac{m^3}{s}$ )
mass flow rate: the mass of fluid that passes through a section of pipe in a given amount of time. (unit $=\frac{\mathrm{kg}}{\mathrm{s}}$ )
Continuity
If a pipe has only one inlet and one outlet, all of the fluid that flows in must flow out, which means the volumetric flow rate through the pipe $\frac{v}{t}$ must be constant.
Because volume is area times length, we can write the volumetric flow rate as:
$
\frac{v}{t}=\frac{A d}{t}
$
Assuming the velocity is constant through a section of the pipe as long as the size and elevation are not changing, we can substitute $v=\frac{d}{t}$, giving:
$
\frac{V}{t}=\frac{A d}{t}=A \cdot \frac{d}{t}=A v=\text { constant }
$
Assuming the velocity is constant through a section of the pipe as long as the size and elevation are not changing, we can substitute $v=\frac{d}{t}$, giving:
$
\frac{V}{t}=\frac{A d}{t}=A \cdot \frac{d}{t}=A v=\text { constant }
$
If the volumetric flow rate remains constant but the diameter of the pipe changes:
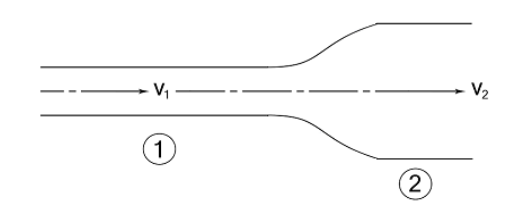
In order to squeeze the same volume of fluid through a narrower opening, the fluid needs to flow faster. Because Av must be constant, the cross-sectional area times the velocity in one section of the pipe must be the same as the cross-sectional velocity in the other section.
$
\begin{aligned}
A v & =\text { constant } \\
A_1 v_1 & =A_2 v_2
\end{aligned}
$
This equation is called the continuity equation, and it is one of the important tools that you will use to solve these problems.
Dynamic Pressure
When a fluid is flowing, the fluid must have kinetic energy, which equals the work that it takes to move that fluid.
Recall the equations for work and kinetic energy:
$
\begin{aligned}
& K=\frac{1}{2} m v^2 \\
& W=\Delta K=F_{\|} d
\end{aligned}
$
Combining these (the work-energy theorem) gives $\frac{1}{2} m v^2=F_{\|} d$.
Solving $P_D=\frac{F}{A}$ for force gives $F=P_D A$. Substituting this into the above equation gives:
$
\frac{1}{2} m v^2=F_{\|} d=P_D A d
$
Rearranging the above equation to solve for dynamic pressure gives the following. Because volume is area times distance $(V=A d)$, we can then substitute $V$ for $A d$ :
$
P_D=\frac{\frac{1}{2} m v^2}{A d}=\frac{\frac{1}{2} m v^2}{V}
$
Finally, rearranging $\rho=\frac{m}{V}$ to solve for mass gives $m=\rho V$. This means our equation becomes:
$
\begin{aligned}
& P_D=\frac{\frac{1}{2} m v^2}{v}=\frac{\frac{1}{2} \rho / v^2}{N}=\frac{1}{2} \rho v^2 \\
& P_D=\frac{1}{2} \rho v^2
\end{aligned}
$
Bernoulli’s Principle
Bernoulli’s Principle, named for Dutch-Swiss mathematician Daniel Bernoulli states that the pressures in a moving fluid are caused by a combination of:
- The hydrostatic pressure: $P_H=\rho g h$
- The dynamic pressure: $P_D=\frac{1}{2} \rho v^2$
- The “external” pressure, which is the pressure that the fluid exerts on its surroundings. (This is the pressure we would measure with a pressure gauge.)
A change in any of these pressures affects the others, which means:
$
\begin{aligned}
P_{\text {ext. }}+P_H+P_D & =\text { constant } \\
P_{\text {ext. }}+\rho g h+\frac{1}{2} \rho v^2 & =\text { constant }
\end{aligned}
$
The above equation is Bernoulli’s equation.
For example, consider the following situation:
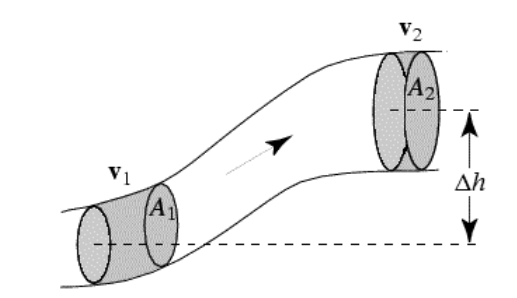
- The velocity of the fluid is changing (because the cross-sectional area is changing-remember the continuity equation $A_1 v_1=A_2 v_2$ ). This means the dynamic pressure, $P_D=\frac{1}{2} \rho v^2$ is changing.
- The height is changing, which means the hydrostatic pressure, $P_H=\rho g h$ is changing.
- The external pressures will also be different, in order to satisfy Bernoulli’s Law.
This means Bernoulli’s equation becomes:
$
P_1+\rho g h_1+\frac{1}{2} \rho v_1^2=P_2+\rho g h_2+\frac{1}{2} \rho v_2^2
$
Note particularly that Bernoulli’s equation tells us that increasing the fluid velocity
$(v)$ increases the dynamic pressure. (If $v$ increases, then $P_D=\frac{1}{2} \rho v^2$ increases.)
This means if more of the total pressure is in the form of dynamic pressure, that means the hydrostatic and/or external pressures will be less.
Consider the following example:
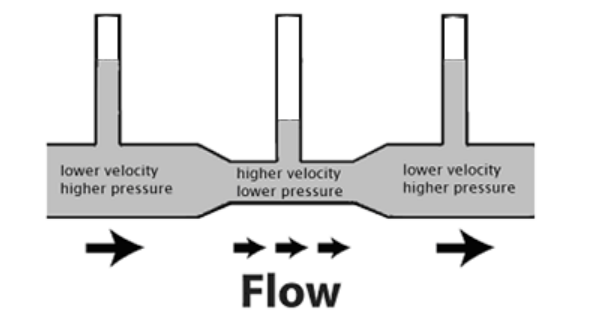
This pipe is horizontal, which means $h$ is constant; therefore $\rho g h$ is constant. This means that if $\frac{1}{2} \rho v^2$ increases, then pressure $(P)$ must decrease so that $P_{\text {ext. }}+\rho g h+\frac{1}{2} \rho v^2=$ constant
Although Bernoulli published his principle in 1738 , the application to fluids in constricted channels was not published until 1797 by Italian physicist Giovanni Venturi. The above apparatus is named after Venturi and is called a Venturi tube.
Torricelli’s Theorem
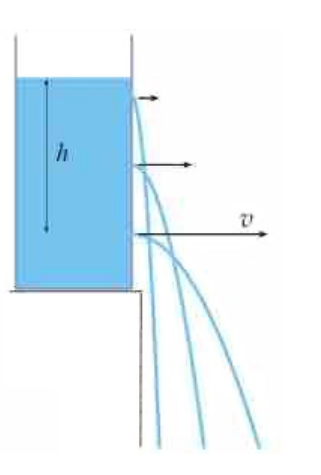
A special case of Bernoulli’s Principle was discovered almost 100 years earlier, in 1643 by Italian physicist and mathematician Evangelista Torricelli. Torricelli observed that in a container with fluid effusing (flowing out) through a hole, the more fluid there is above the opening, the faster the fluid comes out.
Torricelli found that the velocity of the fluid was the same as the velocity would have been if the fluid were falling straight down, which can be calculated from the change of gravitational potential energy to kinetic energy:
$
\begin{aligned}
\frac{1}{2} p g v^2 & =m g g \\
v^2 & =2 g h \\
v & =\sqrt{2 g h}
\end{aligned}
$
Torricelli’s theorem can also be derived from Bernoulli’s equation”:
$
P_1+\rho g h_1+\frac{1}{2} \rho v_1^2=P_2+\rho g h_2+\frac{1}{2} \rho v_2^2
$
- The external pressures $\left(P_1\right.$ and $P_2$ are both equal-atmospheric pressure-so they cancel.
- The fluid level is going down slowly enough that the velocity of the fluid inside the container $\left(v_1\right)$ is essentially zero.
- Once the fluid exits the container, the hydrostatic pressure is zero $\left(\rho g h_2=0\right)$. This leaves us with:
$
\begin{aligned}
\rho g h_1 & =\frac{1}{2} \rho v_2^2 \\
2 g h_1 & =v_2^2 \\
\sqrt{2 g h_1} & =v_2
\end{aligned}
$
We could do a similar proof from the kinematic equation: $v^2-v_o^2=2 a d$
Substituting $a=g, d=h$, and $v_o=0$ gives $v^2=2 g h$ and therefore $v=\sqrt{2 g h}$
* On the AP ${ }^{\oplus}$ Physics exam, you must start problems from equations that are on the formula sheet. This means you may not use Torricelli’s Theorem on the exam unless you first derive it from Bernoulli’s Equation.
The decrease in pressure caused by an increase in fluid velocity explains one of the ways in which an airplane wing provides lift:
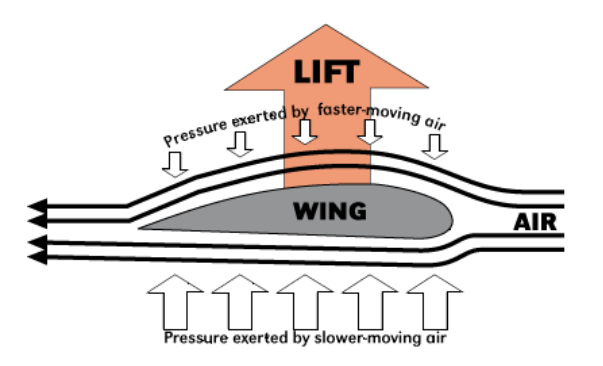
(Of course, most of an airplane’s lift comes from the fact that the wing is inclined with an angle of attack relative to its direction of motion, an application of Newton’s third law.)
A common demonstration of Bernoulli’s Law is to blow across a piece of paper:
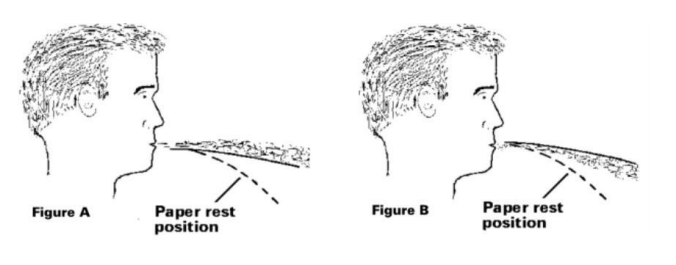
The air moving across the top of the paper causes a decrease in pressure, which causes the paper to lift.
Sample Problems:
Q: A fluid in a pipe with a diameter of $0.40 \mathrm{~m}$ is moving with a velocity of $0.30 \frac{\mathrm{m}}{\mathrm{s}}$. If the fluid moves into a second pipe with half the diameter, what will the new fluid velocity be?
Answer/Explanation
A: The cross-sectional area of the first pipe is:
$
A_1=\pi r^2=(3.14)(0.20)^2=0.126 \mathrm{~m}^2
$
The cross-sectional area of the second pipe is:
$
A_2=\pi r^2=(3.14)(0.10)^2=0.0314 \mathrm{~m}^2
$
Using the continuity equation:
$
\begin{aligned}
A_1 v_1 & =A_2 v_2 \\
A_1 v_1=A_2 v_2(0.126)(0.30) & =(0.0314) v_2 \\
v_2 & =1.2 \frac{\mathrm{m}}{\mathrm{s}}
\end{aligned}
$
Q: A fluid with a density of $1250 \frac{\mathrm{kg}}{\mathrm{m}^3}$ has a pressure of $45000 \mathrm{~Pa}$ as it flows at $1.5 \frac{\mathrm{m}}{\mathrm{s}}$ through a pipe. The pipe rises to a height of $2.5 \mathrm{~m}$, where it connects to a second, smaller pipe. What is the pressure in the smaller pipe if the fluid flows at a rate of $3.4 \frac{\mathrm{m}}{\mathrm{s}}$ through it?
Answer/Explanation
A:
$
\begin{aligned}
P_1+\rho g h_1+\frac{1}{2} \rho v_1^2 & =P_2+\rho g h_2+\frac{1}{2} \rho v_2^2 \\
45000+(1250)(10)(0)+\left(\frac{1}{2}\right)(1250)(1.5)^2 & =P_2+(1250)(10)(2.5)+\left(\frac{1}{2}\right)(1250)(3.4)^2 \\
45000+1406 & =P_2+31250+7225 \\
P_2 & =7931 \mathrm{~Pa}
\end{aligned}
$