Topics covered in this chapter:
Electromagnetic Waves
Notes:
electromagnetic wave: a transverse, traveling wave that is caused by oscillating electric and magnetic fields.
Electromagnetic waves travel through space and do not require a medium. The electric field creates a magnetic field, which creates an electric field, which creates another magnetic field, and so on. The repulsion from these induced fields causes the wave to propagate.
Electromagnetic waves (such as light, radio waves, etc.) travel at the speed of light. The speed of light depends on the medium it is traveling through, but it is a constant within its medium (or lack thereof), and is denoted by the letter ” $c$ ” in equations. In a vacuum, the speed of light is:
$
c=3.00 \times 10^{8 \mathrm{~m} / \mathrm{s}}=186,000 \text { miles per second }
$
Recall that the speed of a wave equals its frequency times its wavelength:
$
c=\lambda f
$
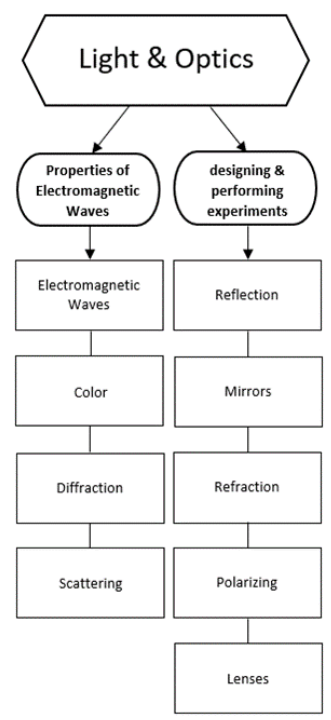
electromagnetic spectrum: the entire range of possible frequencies and wavelengths for electromagnetic waves. The waves that make up the electromagnetic spectrum are shown in the diagram below:
The energy $(E)$ that a wave carries is proportional to the frequency. (Think of it as the number of bursts of energy that travel through the wave every second.) For electromagnetic waves (including light), the constant of proportionality is Planck’s constant (named after the physicist Max Planck), which is denoted by a script $h$ in equations.
The energy of a wave is given by the Planck-Einstein equation:
$
E=h f=\frac{h c}{\lambda}
$
where $E$ is the energy of the wave in Joules, $f$ is the frequency in $\mathrm{Hz}, h$ is Planck’s constant, which is equal to $6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}, c$ is the speed of light, and $\lambda$ is the wavelength in meters.
Antennas
An antenna is a piece of metal that is affected by electromagnetic waves and is used to amplify waves of specific wavelengths. The optimum length for an antenna is either the desired wavelength, or some fraction of the wavelength such that one wave is an exact multiple of the length of the antenna. (E.g., good lengths for an antenna could be $1 / 2,1 / 4,1 / 8$, etc. of the wavelength.)
Sample problem:
Q: What is the wavelength of a radio station that broadcasts at $98.5 \mathrm{MHz}$ ?
Answer/Explanation
A:
$
\begin{aligned}
c & =\lambda f \\
3.00 \times 10^8 & =\lambda\left(9.85 \times 10^7\right) \\
\lambda & =\frac{3.00 \times 10^8}{9.85 \times 10^7}=3.05 \mathrm{~m}
\end{aligned}
$
Q: What would be a good length for an antenna that might be used to receive this radio station?
A: $3.05 \mathrm{~m}$ (about 10 feet) is too long to be practical for an antenna. Somewhere between half a meter and a meter is a good size.
$1 / 4$ wave would be $0.76 \mathrm{~m}(76 \mathrm{~cm})$, which would be a good choice.
Color
Notes:
Light with frequencies/wavelengths in the part of the spectrum that the eye can detect is called visible light.
color: the perception by the human eye of how a light wave appears, based on its wavelength/frequency.
How We See Color
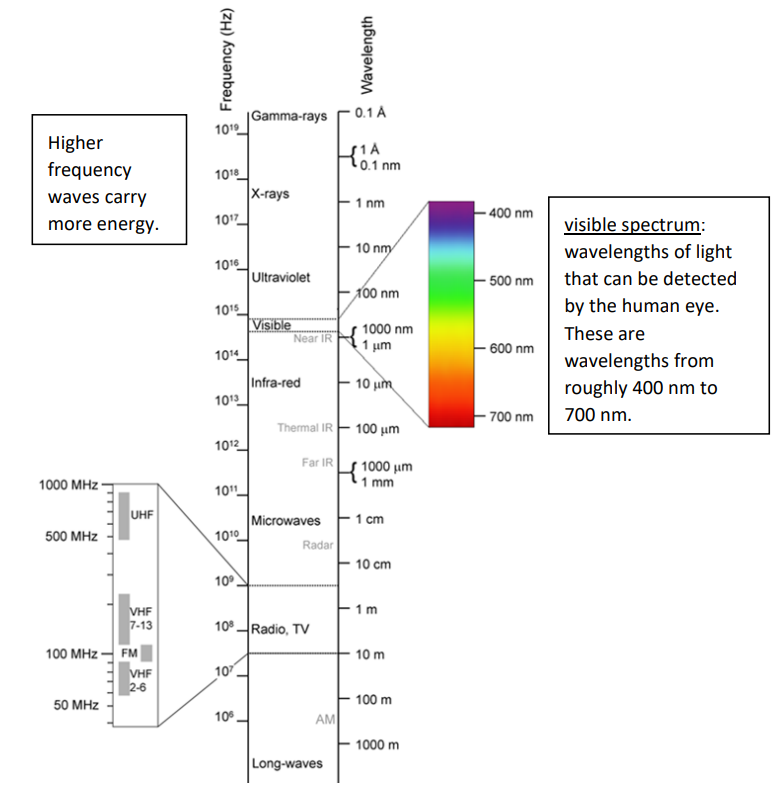
Humans (and other animals) have two types of cells in our retina that respond to light:
Rod cells resolve the physical details of images. Cone cells are responsible for distinguishing colors. Rod cells can operate in low light, but cone cells need much more light; this is why we cannot see colors in low light.
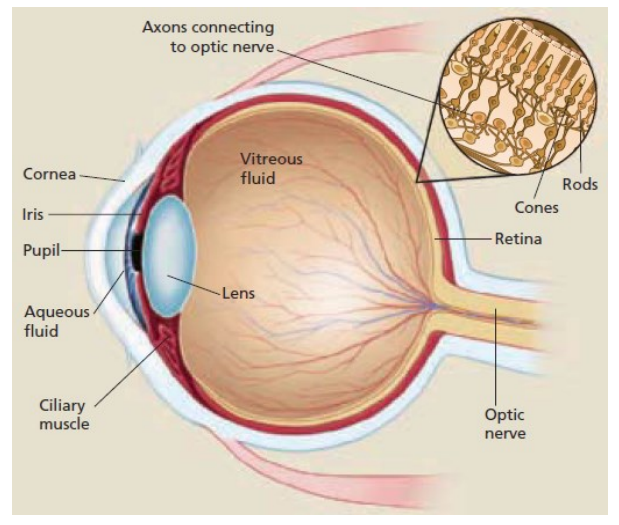
There are three different types of cone cells in our eyes, called ” $\mathrm{S}^{\prime \prime}, ” \mathrm{M}^{\prime \prime}$, and ” $\mathrm{L}$ “, which stand for “short,” “medium,” and “long.” Each type of cone cells responds to different wavelengths of light, having a peak (maximum) absorbance in a different part of the visible spectrum:
For example, light with a wavelength of $400-450 \mathrm{~nm}$ appears blue to us, because most of the response to this light is from the $S$ cells, and our brains are wired to perceive this response as blue color. Light with a wavelength of around $500 \mathrm{~nm}$ would stimulate mostly the $M$ cells and would appear green. Light with a wavelength of around $570 \mathrm{~nm}$ would stimulate the $M$ and $L$ cells approximately equally. When green and red receptors both respond, our brains perceive the color as yellow.
Colorblindness occurs when a genetic mutation causes a deficiency or absence of one or more types of cone cells. Most common is a deficiency in the expression of $\mathrm{M}$ cone cells, which causes red-green colorblindness. This means that a person with red-green colorblindness would see both colors as red.
Because colorblindness is recessive and the relevant gene is on the X-chromosome, red-green colorblindness is much more common in men than in women.
Direct Light: Additive Mixing
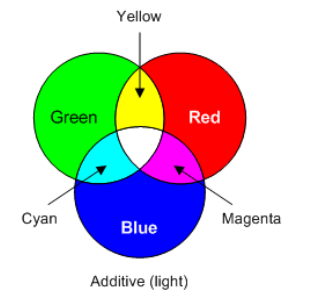
Because our cone cells respond to red, green, and blue light, we call these colors the primary colors of light. Other colors can be made by mixing different amounts of these colors, thereby stimulating the different types of cone cells to different degrees. When all colors are mixed, the light appears white.
primary color: light that excites only one type of cone cell. The primary colors of light are red, green, and blue.
secondary color: light that is a combination of exactly two primary colors. The secondary colors of light are cyan, magenta, and yellow.
Reflected Light: Subtractive Mixing
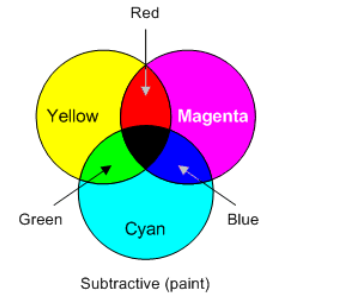
When light shines on an object, properties of that object cause it to absorb certain wavelengths of light and reflect others. The wavelengths that are reflected are the ones that make it to our eyes, causing the object to appear that color.
pigment: a material that changes the color of reflected light by absorbing light with specific wavelengths.
primary pigment: a material that absorbs light of only one primary color (and reflects the other two primary colors). The primary pigments are cyan, magenta, and yellow. Note that these are the secondary colors of light.
secondary pigment: a pigment that absorbs two primary colors (and reflects the other). The secondary pigments are red, green, and blue. Note that these are the primary colors of light.
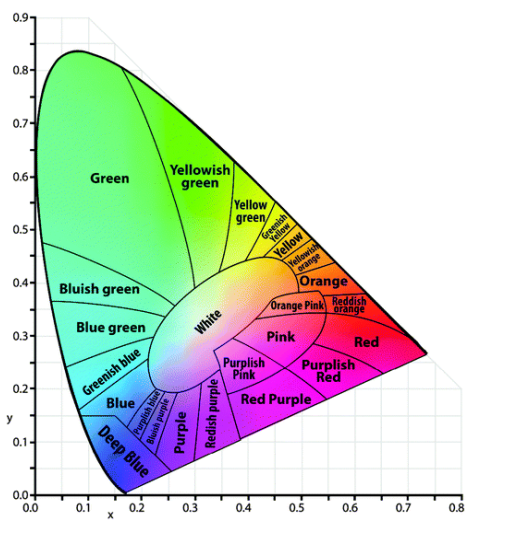
Of course, our perception of color is biological, so mixing primary colors is not a simple matter of taking a weighted average of positions on the color wheel. The relationship between the
fractions of primary colors used to produce a color and the color perceived is called chromaticity. The following diagram shows the colors that would be produced by varying the
intensities of red, green, and blue light. On this graph, the x-axis is the fraction (from 0 – 1) of red light, the y-axis is the fraction of green light, and the fraction of blue is implicit [1 – (red + green)].
Notice that equal fractions (0.33) of red, green and blue light would produce white light. To show the effects of mixing two colors, plot each color’s position on the graph and connect them with a line. The linear distance along that line shows the proportional effects of mixing. (E.g., the midpoint would represent the color generated by 50% of each of the source colors.) This method is how fireworks manufacturers determine the mixtures of different compounds that will produce the desired colors.
Reflection
Notes:
reflection: when a wave “bounces” off an object and changes direction. specular reflection: reflection from a smooth surface.
diffuse reflection: reflection from a rough surface.
virtual image: a perceived image that appears to be the point of origin of photons (rays of light) that diverge. Because light is reflected back from a mirror (i.e., light cannot pass through it), a virtual image is one that appears behind (or “inside”) the mirror. A virtual image is what you are used to seeing in a mirror.
real image: a reflected image that is created by photons (rays of light) that converge. Because light is reflected back from a mirror (i.e., light cannot pass through it), a real image is one that appears in front of the mirror. A real image created by a mirror looks like a hologram.
A rule of thumb that works for both mirrors and lenses is that a real image is produced by the convergence of actual rays of light. A virtual image is our perception of where the rays of light appear to have come from.
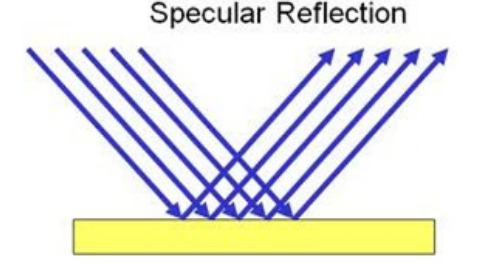
Specular reflection: reflection from a smooth surface, such as a mirror. If the photons of light from the source are parallel when they strike the surface, they will also be parallel when they
reflect from the surface. This results in a reflected image that appears to be the same size, shape, and distance from the surface as the original object.
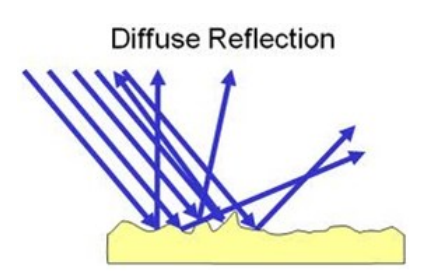
Diffuse reflection : reflection from a rough surface, such as a wall. Light striking a rough surface will illuminate the surface. However, because the reflected light rays are not parallel, the reflected light does not create a reflected image of the object.
mirror: a surface that causes specular reflection. An object that was not made to be a mirror but behaves like one is often called a mirrored surface.
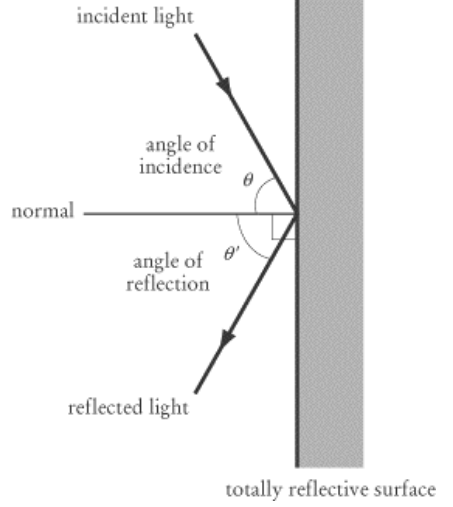
When light waves strike a mirrored surface at an angle (measured from the perpendicular or “normal” direction), they are reflected at the same angle away from the perpendicular. The most common statement of this concept is “The angle of incidence equals the angle of reflection.”
This can be stated mathematically as either $\theta=\theta^{\prime}$ or $\theta_i=\theta_r$.
Mirrors
Notes:
mirror: a surface that light rays reflect from at the same angle the light rays came from.
convex: an object that curves outward.
concave: an object that curves inward.
flat: an object that is neither convex nor concave. focal point: the point at which parallel rays striking a mirror converge. principal axis: a line perpendicular to a mirror (i.e., with an angle of incidence of $0^{\circ}$ ) such that a ray of light is reflected back along its incident (incoming) path.
The principal axis is often shown as a single horizontal line, but every point on a mirror has a principal axis.
Flat Mirrors
With a flat mirror, the light reflected off the object (such as the person in the picture below) bounces off the mirror and is reflected back. Because our eyes and the part of our brains that decode visual images can’t tell that the light has been reflected, we “see” the reflection of the object in the mirror
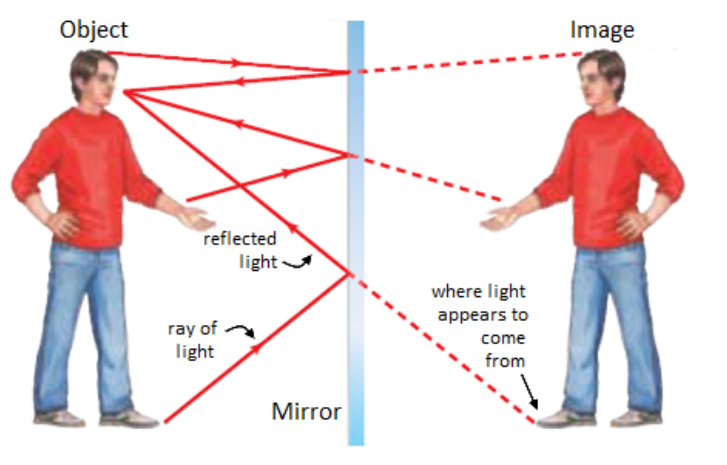
If the mirror is flat, the reflection is the same size and the same distance from the mirror as the actual object. However, the image looks like it is reversed horizontally, but not vertically.
It would seem that the mirror “knows” to reverse the image horizontally but not vertically. (Of course this is not true. If you want the mirror to reverse the image vertically, all you need to do is put the mirror on the floor.) What is actually happening is that light is reflected straight back from the mirror. Anything that is on your right will also be on the right side of the image (from your point of view; if the image were actually a person, this would be the other person’s left). Anything that is on top of you will also be on top of the image as you look at it.
What the mirror is doing is the same transformation as flipping a polygon over the $y$ axis. The reversal is actually front-to-back (where “front” means closer to the mirror and “back” means farther away from it).
Convex and Concave Mirrors
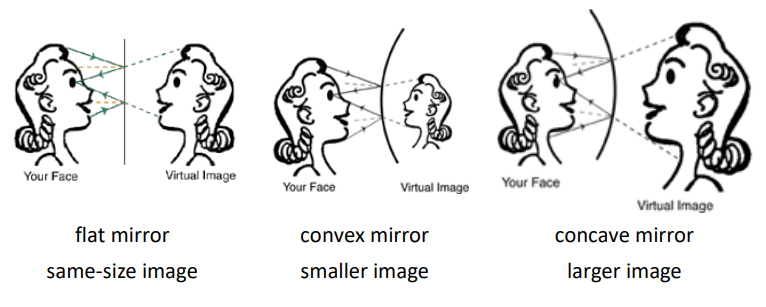
With a convex mirror (curved outwards), the reflected rays diverge (get farther apart). When this happens, it makes the reflection appear smaller. In a concave mirror (curved inwards), the reflected rays converge (get closer together). When this happens, it makes the reflection appear larger.

One place you have probably seen convex mirrors is the passenger-side mirrors in cars. The mirror is slightly convex in order to show a wider field of view. However, this makes the image smaller and appear farther away. If you wear makeup, you may have used a concave mirror. The larger image makes it easier to see small details. (However, it is important to remember that those details are smaller than they appear!)
Focal Point
The focal point or focus of a mirror is the point where the rays of reflected light converge. For a spherical mirror (one in which the shape of the mirror is the surface of a sphere), the focus is halfway between the surface of the mirror and the center of the sphere. This means the distance from the mirror to the focus $(f)^*$ is half of the radius of curvature $\left(r_c\right)$ :
$
f=\frac{r_c}{2} \quad \text { or } \quad r_c=2 f
$
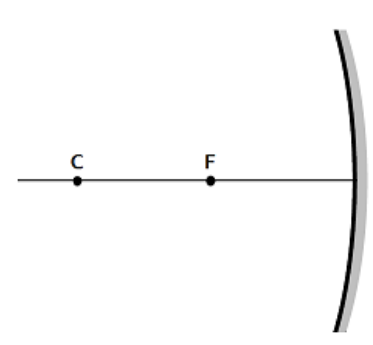
In an introductory physics class, the focus of a curved mirror is often described as a single point, as in the following diagram.
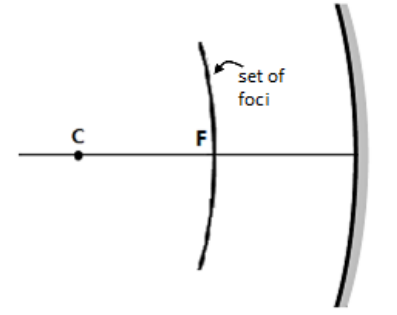
However, is important to remember that a principal axis (a line perpendicular to the mirror) can be drawn from any point along the surface of the mirror. This means that the focus is not a single point, but rather the set of all points that are halfway between the center of the sphere and the surface of the mirror:
” Some physics textbooks use the variables $d_0, d_i$, and $d_f$ for distances to the object, image, and focus, respectively. These notes use the variables $s_0, s_i$, and $f$ in order to be consistent with the equation sheet provided by the College Board for the AP® Physics 2 exam.
Ray Tracing
An intuitive way of finding the location, size and orientation of an image in a mirror is to draw (trace) the rays of light to see where they converge.
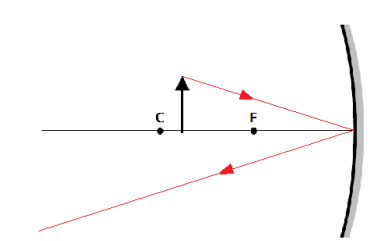
1. A ray of light that hits the mirror anywhere on a principal axis is reflected back at the same angle relative to that principal axis. (The angle of incidence relative to the principal axis equals the angle of reflection.)
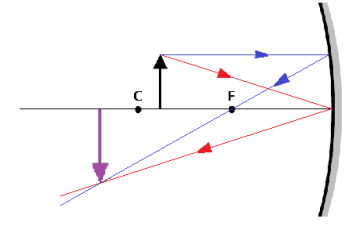
2. A ray of light that hits the mirror parallel to the principal axis is reflected directly toward or away from the focus.
3. If you draw a pair of rays from the top of the object as described by #1 and #2 above, the intersection will be at the top of the image of the object.
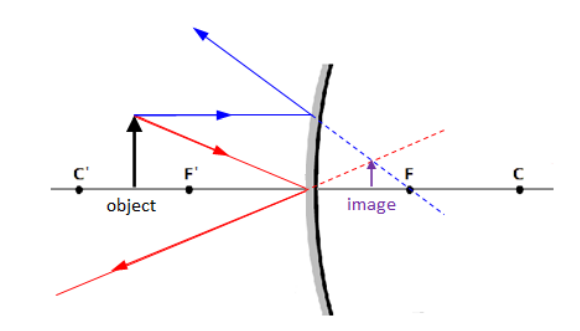
Convex Mirrors
For a convex mirror, the image is always virtual (behind the mirror) and is always smaller than the object:
Concave Mirrors
For a concave mirror, what happens with the image changes depending on where the object is relative to the center of curvature and the focus, as shown by ray tracing in each the following cases.
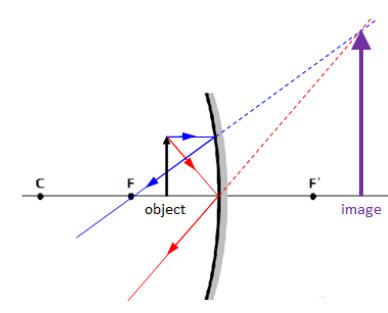
2. If the object is at the focus, there is no image because the rays do not converge.
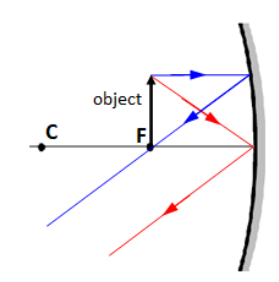
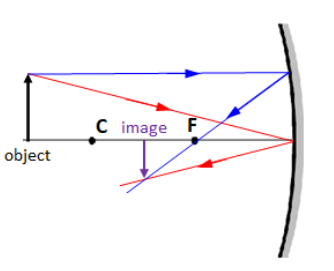
3. If the object is between the focus and the center of curvature, you see a real image (in front of the mirror) that is behind the object, inverted (upside-down), and larger.
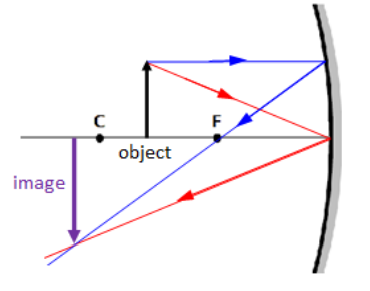
4. If the object is at the center of curvature, you see a real, inverted image that is the same size and same distance from the mirror as the object.
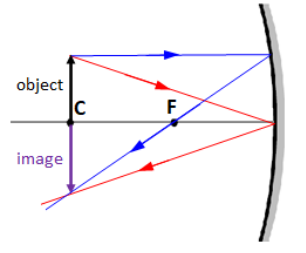
5. If the object is farther from the mirror than the center of curvature, you see a real, inverted image that is smaller and closer to the mirror than the object.
Equations
The distance from the mirror to the focus $(f)$ can be calculated from the distance to the object $\left(s_o\right)$ and the distance to the image $\left(s_i\right)$, using the following equation:
$
\frac{1}{s_o}+\frac{1}{s_i}=\frac{1}{f}
$
Distances for the image $\left(s_i\right)$ and focus $(f)$ are positive in front of the mirror (where a real image would be), and negative behind the mirror (where a virtual image would be).
The height of the image $\left(h_i\right)$ can be calculated from the height of the object $\left(h_o\right)$ and the two distances $\left(s_i\right.$ and $\left.s_o\right)$, using the following equation:
$
M=\frac{h_i}{h_o}=-\frac{s_i}{s_o}
$
A positive value for $h_i$ means the image is upright (right-side-up), and a negative value for $h_i$ means the image is inverted (upside-down).
magnification: the ratio of the size of the image to the size of the object.
If $M>1$, the image is larger than the object. (For example, if $M=2$, then the image is twice as large as the object.) If $M=1$, the object and image are the same size. If $M<1$, the image is smaller. Finally, note that in a mirror, virtual images are always upright, and real images are always inverted.
Sample Problem:
Q: An object that is $5 \mathrm{~cm}$ high is placed $9 \mathrm{~cm}$ in front of a spherical convex mirror. The radius of curvature of the mirror is $10 \mathrm{~cm}$. Find the height of the image and its distance from the mirror. State whether the image is real or virtual, and upright or inverted.
Answer/Explanation
A: The mirror is convex, which means the focus is behind the mirror. This is the side where a virtual image would be, so the distance to the focus is therefore negative. The distance to the focus is half the radius of curvature, which means $f=-5 \mathrm{~cm}$. From this information, we can find the distance from the mirror to the image $\left(s_i\right)$ :
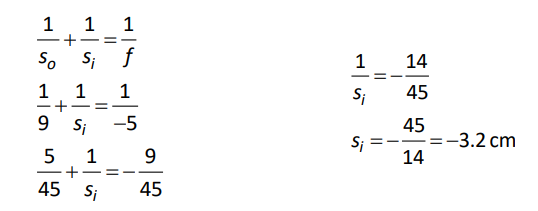
The value of $-3.2 \mathrm{~cm}$ means the image is a virtual image located $3.2 \mathrm{~cm}$ behind the mirror.
Now that we know the distance from the mirror to the image, we can calculate the height of the image $\left(h_i\right)$ :
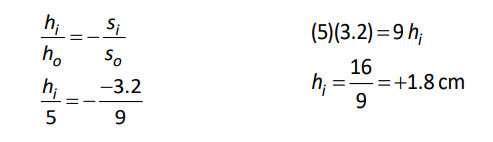
The image is 1.8 cm high. Because the height is a positive number, this means the image is upright (right-side-up).
Refraction
Notes:
refraction: a change in the velocity and direction of a wave as it passes from one medium to another. The change in direction occurs because the wave travels at different velocities in the different media.
index of refraction: a number that relates the velocity of light in a medium to the velocity of light in a vacuum.
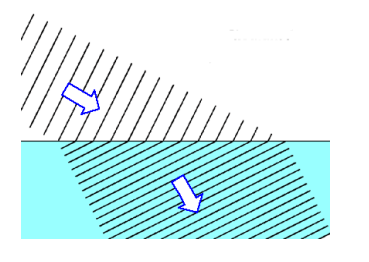
When light crosses from one medium to another, the difference in velocity of the waves causes the wave to bend. For example, in the picture below, the waves are moving faster in the upper medium. As they enter the lower medium, they slow down. Because the part of the wave that enters the medium soonest slows down first, the angle of the wave changes as it crosses the boundary. When the waves slow down, they are bent toward the normal (perpendicular), as in the following diagram:
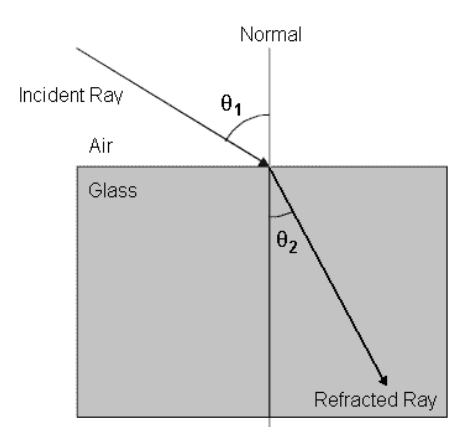
The index of refraction of a medium is the velocity of light in a vacuum divided by the velocity of light in the medium:
$
n=\frac{c}{v}
$
Thus the larger the index of refraction, the more the medium slows down light as it passes through.
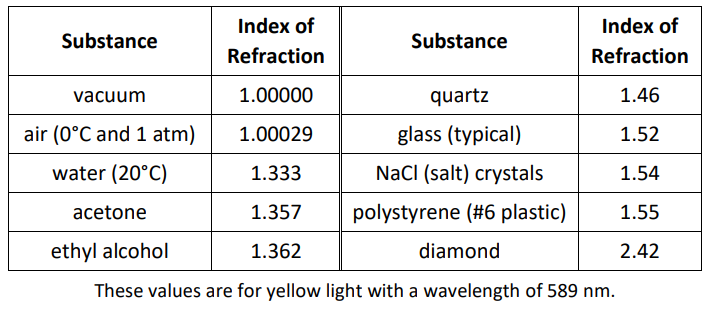
The index of refraction for some substances is given below.
For light traveling from one medium into another, the ratio of the speeds of light is related inversely to the ratio of the indices of refraction, as described by Snell’s Law (named for the Dutch astronomer Willebrord Snellius):
$
\frac{\sin \theta_1}{\sin \theta_2}=\frac{v_1}{v_2}=\frac{n_2}{n_1}
$
The more familiar presentation of Snell’s Law is:
$
n_1 \sin \theta_1=n_2 \sin \theta_2
$
Sample Problem:
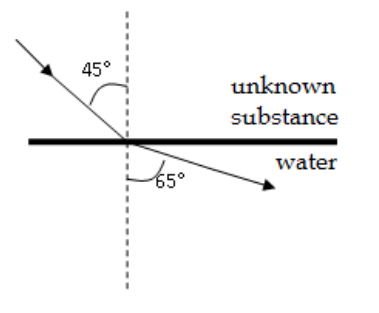
Q: Incident light coming from an unknown substance strikes water at an angle of $45^{\circ}$. The light refracted by the water at an angle of $65^{\circ}$, as shown in the diagram at the right. What is the index of refraction of the unknown substance?
Answer/Explanation
A: Applying Snell’s Law:
$
\begin{aligned}
& n_1 \sin \theta_1=n_2 \sin \theta_2 \\
& n_1 \sin \left(45^{\circ}\right)=(1.33) \sin \left(65^{\circ}\right) \\
& n_1=\frac{(1.33) \sin 65^{\circ}}{\sin 45^{\circ}}=\frac{(1.33)(0.906)}{0.707}=1.70
\end{aligned}
$
Prisms
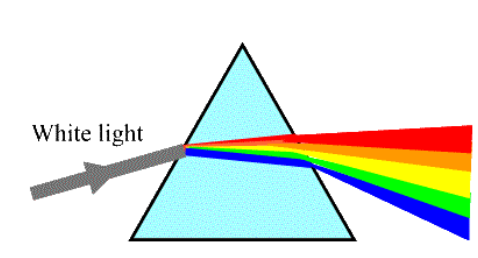
The index of refraction of a medium varies with the wavelength of light passing through it. The index of refraction is greater for shorter wavelengths (toward the violet end of the spectrum) and less (closer to 1) for longer wavelengths (toward the red end of the spectrum
prism: an object that refracts light If light passes through a prism (from air into the prism and back out) and the two interfaces are not parallel, the different indices of refraction for the different wavelengths will cause the light to spread out.
When light is bent by a prism, the ratio of indices of refraction is the inverse of the ratio of wavelengths. Thus we can expand Snell’s Law as follows:
$
\frac{\sin \theta_1}{\sin \theta_2}=\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}=\frac{n_2}{n_1}
$
Total Internal Reflection
If a light wave is traveling from a slower medium to a faster one and the angle is so steep that the refracted angle would be $90^{\circ}$ or greater, the boundary acts as a mirror and the light ray reflects off of it. This phenomenon is called total internal reflection:
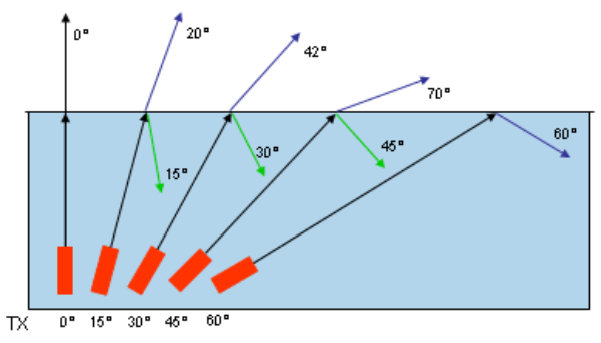
critical angle $\left(\theta_c\right)$ : the angle beyond which total internal reflection occurs.
$
\theta_c=\sin ^{-1}\left(\frac{n_2}{n_1}\right)
$
Total internal reflection is how optical fibers (long strands of optically pure glass with a high index of refraction) are used to transmit information over long distances, using pulses of light.
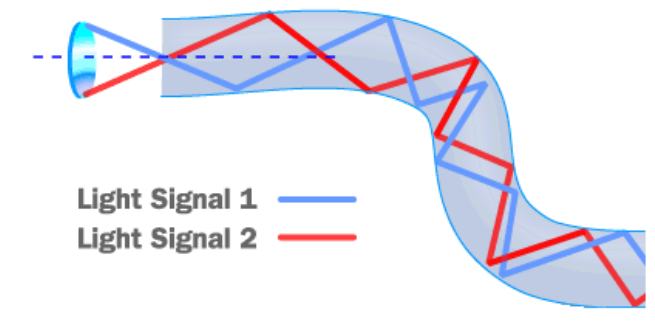
Total internal reflection is also the principle behind speech teleprompters:

The speaker stands behind a clear piece of glass. The image of the speech is projected onto the glass. The text is visible to the speaker, but not to the audience
Rainbows
A rainbow occurs from a combination of refraction, total internal reflection, and a second refraction, with raindrops acting as the prisms.
When this process occurs, different wavelengths of are refracted at different angles. Because colors near the red end of the spectrum have a lower index of refraction, the critical angle is shallower for these wavelengths, and they are reflected at a shallower angle than colors closer to the violet end of the spectrum.
The overall change in the direction of the light after this combination of refractionreflection-refraction (including both refractions as well as the reflection) ranges from approximately $40^{\circ}$ for violet light to approximately $42^{\circ}$ for red light. This difference is what produces the spread of colors in a rainbow, and is why red is always on the outside of the rainbow and violet is always on the inside.
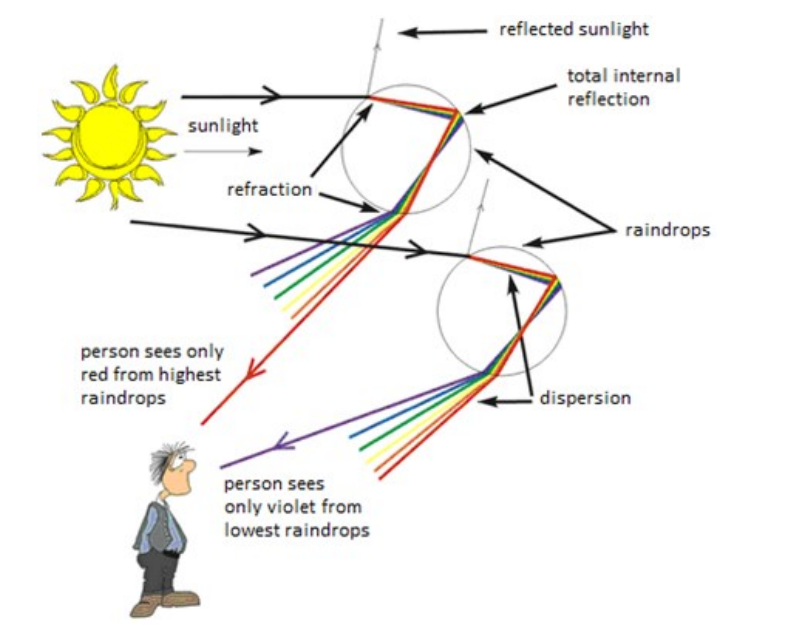
When internal reflection occurs twice on the inside of a raindrop, the result is a second rainbow.
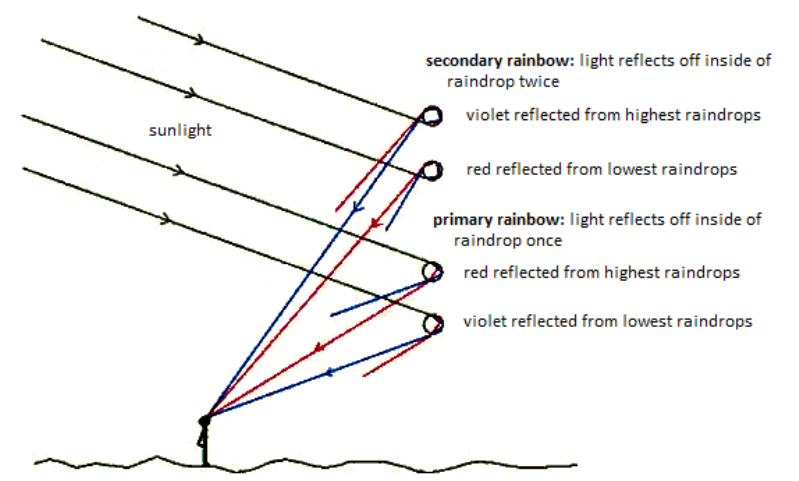
The second rainbow appears above the first because the angle of light exiting the raindrop is greater—varying from 50° for red light to 52.5° for violet light. The second internal reflection reverses the colors, which is why violet is on the outside and red is on the inside in the second rainbow.
This is a picture of a double rainbow in Lynn, Massachusetts. Note that the order of the colors in the second rainbow is reversed.

Note also that the sky is brighter inside the primary rainbow. There are two reasons for this. First, it’s not actually true that each band is only one color of light. Because red light reflects at all angles greater than or equal to $40^{\circ}$, red light is therefore a component of all of the colors inside the red band of the rainbow. The same is true for each of the other colors; inside of the violet band, all wavelengths of visible light are present, and the result is white light. Outside of the red band, no visible light is refracted, which causes the sky outside the rainbow to appear darker.
Second, raindrops scatter light at all wavelengths, and light scattering is also a significant contributing factor to the brightness inside. (See the Scattering topic starting on page 545 for more information.)
You may also notice that because the second rainbow is reversed, the sky is slightly brighter outside of the second rainbow.
Polarization
Notes:
Normally, light (and other electromagnetic waves) propagate in all directions. When the light is passed through a special filter, called a polarizer, it blocks light waves in all but one plane (direction), as shown in the following diagram:
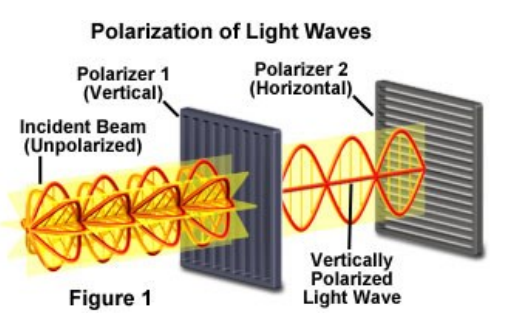
Light that is polarized in this manner is called plane-polarized light.
Note that if you place two polarizers on top of each other and turn them so they polarize in different directions, no light can get through. This is called crossed polarization.
A flat surface can act as a polarizer at certain angles. The Scottish physicist Sir David Brewster derived a formula for the angle of maximum polarization based on the indices of refraction of the two substances:
$
\theta_B=\tan ^{-1}\left(\frac{n_2}{n_1}\right)
$
where:
$
\begin{aligned}
\theta_B= & \text { Brewster’s angle, the angle of incidence at which unpolarized light } \\
& \text { striking a surface is perfectly polarized when reflected. } \\
n_1 \& n_2= & \text { indices of refraction of the two substances }
\end{aligned}
$
The two pictures below were taken with the same camera and a polarizing filter. In the picture on the left, the polarizing filter is aligned with the light reflected off the window. In the picture on the right, the polarizing filter is rotated $90^{\circ}$ so that none of the reflected light from the window can get to the camera lens.

Another example is light reflecting off a wet road. When the sun shines on a wet road at a low angle, the reflected light is polarized parallel to the surface (i.e., horizontally). Sunglasses that are polarized vertically (i.e., that allow only vertically polarized light to pass through) will effectively block most or all of the light reflected from the road.
Yet another example is the light that creates a rainbow. When sunlight reflects off the inside of a raindrop, the angle of incidence is very close to Brewster’s angle. This causes the light that exits the raindrop to be polarized in the same direction as the bows of the rainbow (i.e., horizontally at the top). This is why you cannot see a rainbow through polarized sunglasses!
Lenses
Notes:
Lenses are similar to curved mirrors in that they change the direction of light rays to produce an image of an object that can have a different size, orientation and distance from the mirror relative to the object.
Lenses are different from mirrors in that light passes through them, which means they operate by refraction instead of reflection.
lens: a usually-symmetrical optical device which refracts light in a way that makes the rays of light either converge or diverge.
convex lens: a lens that refracts light so that it converges as it passes through.
concave lens: a lens that refracts light so that it diverges as it passes through.
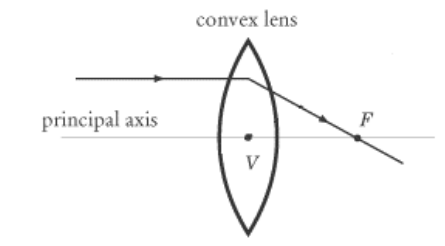
focus or focal point: the point at which light rays converge after passing through the lens.
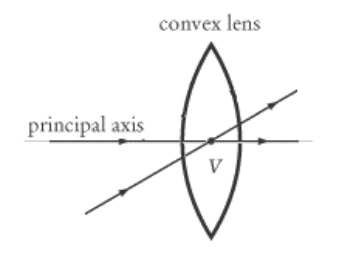
principal axis: a line perpendicular to the surface of the lens, such that light passing through it is refracted at an angle of $0^{\circ}$ (i.e., the direction is not changed).
The principal axis is often shown as a single horizontal line, but every point on the surface of a lens has a principal axis. Note also that if a lens is asymmetrical, its principal axis may be different on each side.
vertex: the point where the principal axis passes through the center of the lens.
real image: an image produced by light rays that pass through the lens. A real image will appear on the opposite side of the lens from the object. A real image is what you are used to seeing through a magnifying glass.
virtual image: an apparent image produced at the point where diverging rays appear to originate. A virtual image will appear on the same side of the lens as the object.
A rule of thumb that works for both mirrors and lenses is that a real image is produced by the convergence of the actual rays of light. A virtual image is our perception of where the rays of light would have come from.
upright image: an image that is oriented in the same direction as the object. (“rightside-up”)
inverted image; an image that is oriented in the opposite direction from the object. (“upside-down”)
Calculations
The equations for lenses are the same as the equations for curved mirrors. Distances are measured from the vertex.
The magnification $(M)$ is the ratio of the height of the image $\left(h_i\right)$ to the height of the object $\left(h_o\right)$, which is equal to the ratio of the distance of the image $\left(s_i\right)$ to distance of the $\operatorname{object}\left(s_0\right)$.
$
M=\frac{h_i}{h_o}=-\frac{s_i}{s_o}
$
As with mirrors, the distance to the image is defined to be positive for a real image, and negative for a virtual image. However, note that with lenses the real image is caused by the rays of light that pass through the lens, which means a real image is behind a lens, where as a real image is in front of a mirror.
Note also that for lenses, this means that the positive direction for the object and the positive for the image are opposite.
As with mirrors, the distance from the vertex of the lens to the focus $(f)$ is defined by the equation:
$
\frac{1}{s_i}+\frac{1}{s_o}=\frac{1}{f}
$
Ray Tracing
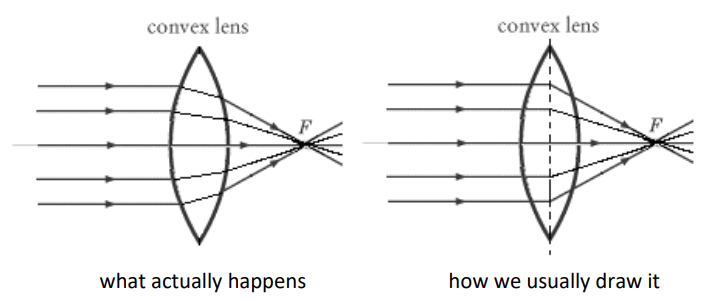
1. Light passing through the vertex of the lens comes out of the lens in the same direction as it entered, as if the lens were not there.
2. Light passing through any part of the lens other than the vertex is refracted through the focus.
Notice that the light is refracted twice, once upon entering the lens and a second time upon entering the air when it exits. For convenience, we usually draw the ray trace as if the light is refracted once when it crosses the center of the lens.
Convex Lenses
A convex lens causes light rays to converge (bend towards each other) as they pass through.
The most familiar use of convex lenses is as a magnifying glass. Note how the bending of the light rays makes the object appear larger
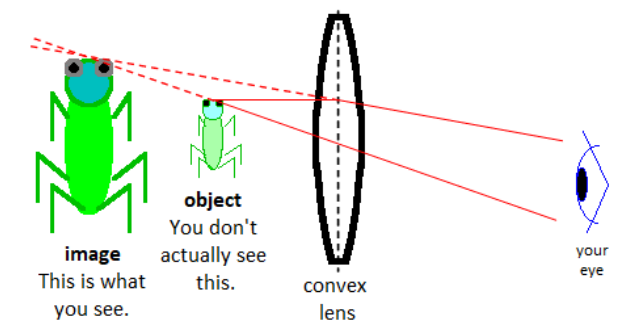
Note also that the lens bends all of the light. Your eyes cannot see the unbent light rays, which means you cannot see the actual object in its actual location; you only see the image.
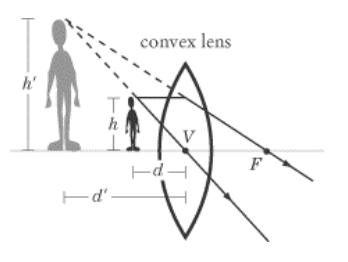
For a convex lens, the focus is always on the opposite side of the lens from the object:
2. If the object is closer than the focus, the image is virtual (on the same side of the lens) and upright (right-side-up).
Concave Lenses
A concave lens causes light rays to diverge (bend away from each other). For a concave lens, the focus is on the same side of the lens as the object.
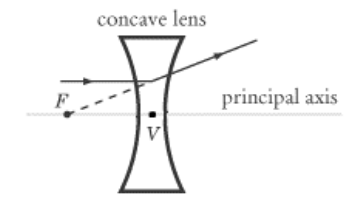
For a concave lens, the image is always virtual (on the same side of the lens) and upright (right-side-up):
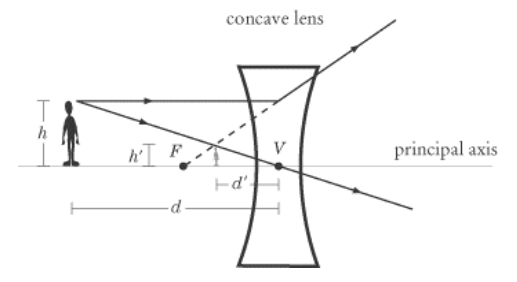
Physiology
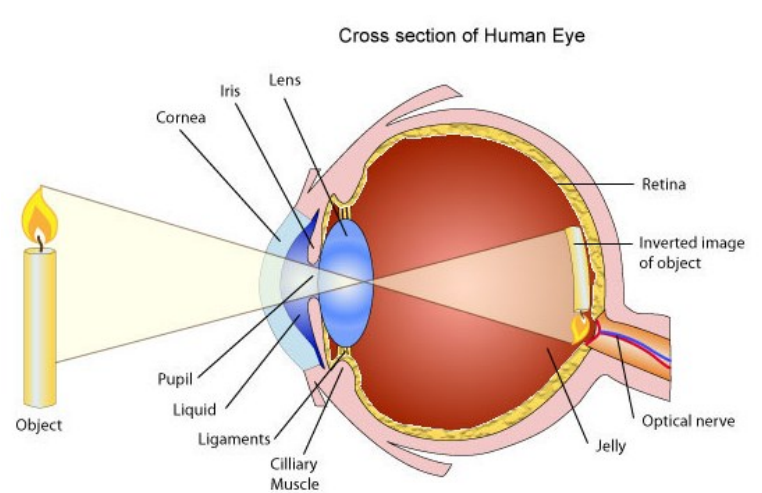
In the human eye, the cornea and lens both act as lenses. However, because the action of the ciliary muscles changes the shape of the lens, the lens is responsible for the exact focal point, which determines what we are focusing our eyes on. When the ciliary muscles relax, the images of distant objects are focused on the retina. When these muscles contract, the focal point moves and closer objects come into focus.
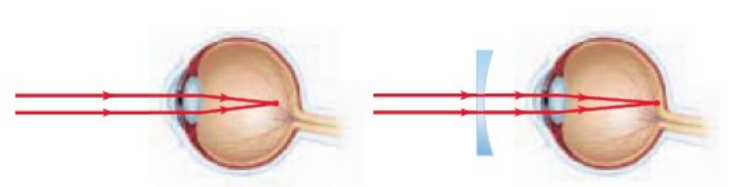
Nearsightedness and Farsightedness
“Nearsighted” means only objects near the eye are in focus; the viewer is unable to focus on distant objects. This happens because the focus of the lens when the ciliary muscles are fully relaxed is in front of the retina. Nearsightedness is corrected by eyeglasses with concave lenses, which move the focal point back to the retina.
Notice that lenses that correct nearsightedness are concave only on the inside. This helps the lenses avoid the “Coke bottle” look.
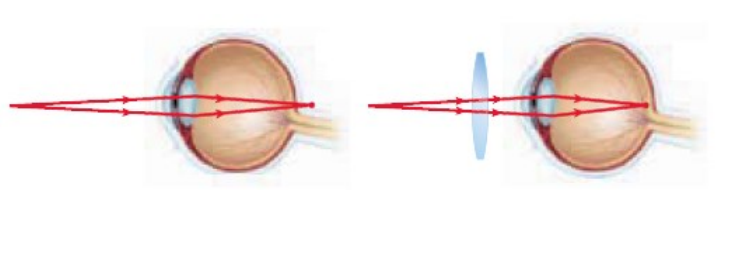
“Farsighted” means only objects far away from the eye are in focus; the viewer is unable to focus on close objects. This happens because the ciliary muscles cannot contract enough to bring the focal point of the lens for light coming from nearby objects onto the retina. Farsightedness is corrected by eyeglasses with convex lenses, which move the focal point forward to the retina.
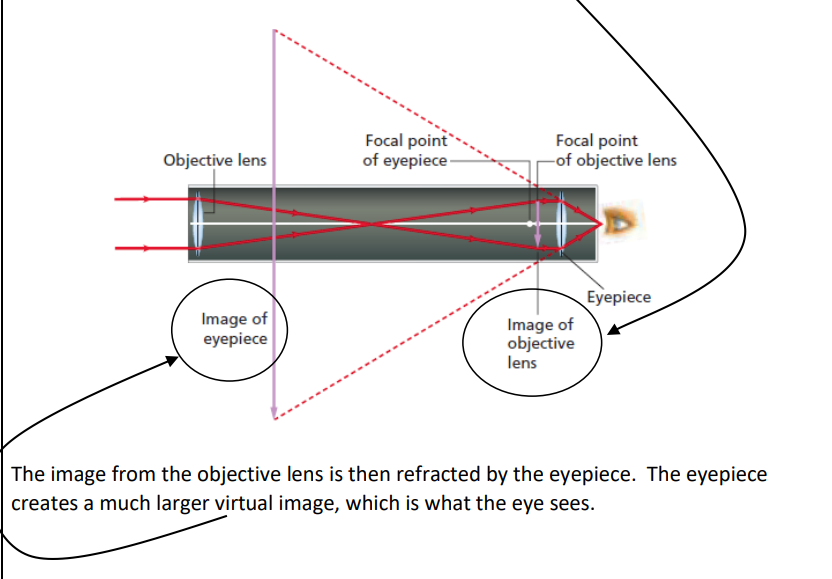
Telescopes
A telescope performs two tasks. The objective lens focuses light from a distant object and creates a virtual image in front of the eyepiece.
Diffraction
Notes:
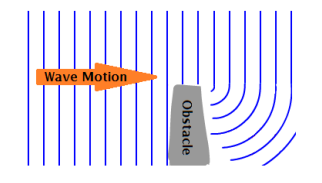
diffraction: the slight bending of a wave as it passes around the edge of an object or through a slit:
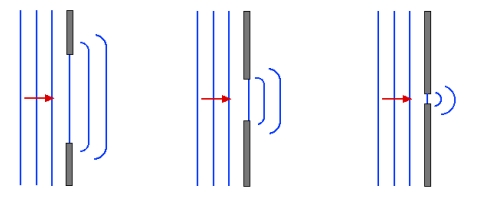
When light passes straight through a wide opening, the rays continue in a straight line. However, if we make the slit so narrow that the width is approximately equal to the wavelength, then the slit effectively becomes a point, and diffractionoccurs in all directions from it.
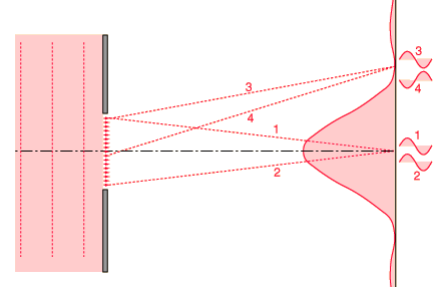
If we shine light through a slit whose thickness is approximately the same order of magnitude as the wavelength, the light can only hit the wall in specific locations.
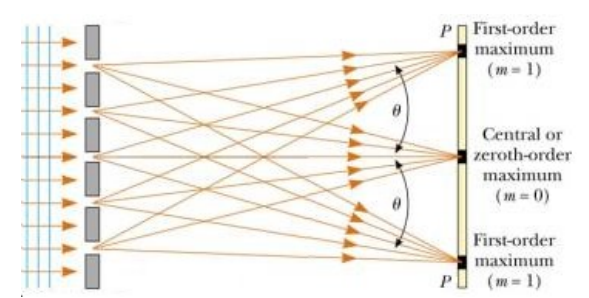
In the this diagram, light travels the same distance for paths 1 and 2 -the same number of wavelengths. Light waves hitting this point will add constructively, which makes the light brighter. However, for paths 3 and 4, path 4 is ½ wavelength longer than path 3. Light taking path 4 is ½ wavelength out of phase with light from path 3. The waves add destructively (cancel), and there is no light:
Farther up or down on the right side will be alternating locations where the difference in path length results in waves that are different by an exact multiple of the wavelength (in phase $=$ constructive interference $=$ bright spots), vs. by a multiple of the wavelength plus $1 / 2$ (out-of-phase $=$ destructive interference $=$ dark spots).
The equation that relates the distance between these regions of constructive interference to the distance between the slits in a diffraction grating is:
$
d \sin \theta_m=m \lambda
$
where:
$m=$ the number of waves that equals the difference in the lengths of the two paths (integer)
$\theta_m=$ the angle of emergence (or angle of deviation) in order for light from one slit to add constructively to light from a neighboring slit that is $m$ wavelengths away.
$d=$ the distance between the slits
$\lambda=$ the wavelength of the light
diffraction grating: a screen with a series of evenly-spaced slits that scatters light in a repeating, predictable pattern
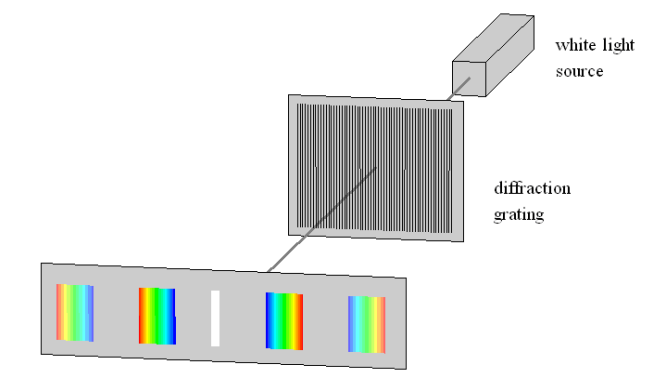
When light shines through a diffraction grating, the following happens:
The patterns of light surrounding the center are the points where the waves of light add constructively. Notice that blue and violet light (with the shortest wavelengths) is diffracted the least and appears closest to the center, whereas red light is diffracted more and appears farther away. This is because shorter waves bend more around the edges of a slit, because they need to turn less far to fit through the slits than longer waves do.
Sample Problem:
Q: Consider three laser pointers: a red laser with a wavelength of $650 \mathrm{~nm}$, a green laser with a wavelength of $532 \mathrm{~nm}$, and a blue laser with a wavelength of $405 \mathrm{~nm}$. If each of these is shone through a diffraction grating with 5000 lines per $\mathrm{cm}$, what will be the angle of emergence for each color?
Answer/Explanation
A: For our diffraction grating, 5000 lines per $\mathrm{cm}$ equals 500000 lines per meter.
$
d=\frac{1}{500000}=2 \times 10^{-6} \mathrm{~m}
$
For the red laser, $650 \mathrm{~nm}$ equals $\lambda=650 \mathrm{~nm}=6.50 \times 10^{-7} \mathrm{~m}$
The equation is:
$
d \sin \theta_m=m \lambda
$
For the red laser at $m=1$, this becomes:
$
\begin{aligned}
& \left(2 \times 10^{-6}\right) \sin \theta=(1)\left(6.50 \times 10^{-7}\right) \\
& \sin \theta=\frac{6.50 \times 10^{-7}}{2 \times 10^{-6}}=0.325 \\
& \theta=\sin ^{-1}(0.325)=19.0^{\circ}
\end{aligned}
$
For the green laser $\left(\lambda=532 \mathrm{~nm}=5.32 \times 10^{-7} \mathrm{~m}\right)$ and the blue laser also at $m=1$
$
\left(\lambda=405 \mathrm{~nm}=4.05 \times 10^{-7} \mathrm{~m}\right) \text { : }
$
$
\begin{aligned}
& \sin \theta=\frac{5.32 \times 10^{-7}}{2 \times 10^{-6}}=0.266 \\
& \sin \theta=\frac{4.05 \times 10^{-7}}{2 \times 10^{-6}}=0.203 \\
& \theta=\sin ^{-1}(0.266)=15.4^{\circ} \\
& \theta=\sin ^{-1}(0.203)=11.7^{\circ} \\
&
\end{aligned}
$
Scattering
Notes:
scattering: a change in the direction of rays of light caused by irregularities in the propagation medium, collisions with small particles, or at the interface between two media.
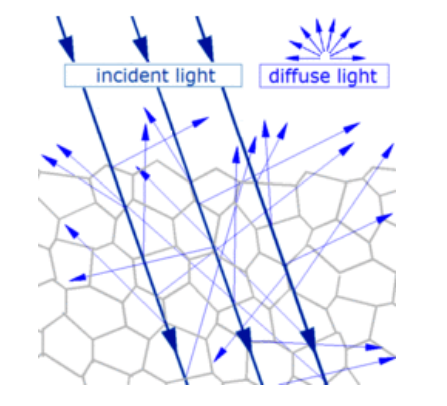
Rayleigh scattering: scattering of light because of collisions with small particles in the medium. Rayleigh scattering is named after the British physicist Lord Rayleigh.
Rayleigh scattering is responsible for the color of the sky. Small particles (0.51 micron) scatter visible light as it passes through Earth’s atmosphere. Because light at the blue and violet end of the spectrum is about five times as likely to be scattered as light at the red end of the spectrum, the majority of the scattered light in our atmosphere is blue.
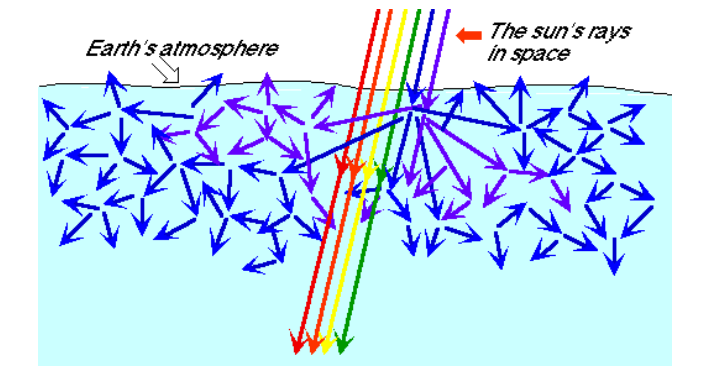
This is also why the sun appears yellow during the day-the combination of red, orange, yellow and green light appears yellow to us.
Water vapor molecules are much larger-ranging in size from 2-5 microns. For these larger particles, the probability of scattering is approximately the same for all wavelengths, which is why clouds appear white.
At sunset, because the angle of the sun is much lower, the light must pass through much more of the atmosphere before we see it. By the time the light gets to our eyes, all of the colors are removed by scattering except for the extreme red end of the spectrum, which is why the sun appears red when it sets.