Topics covered in this chapter:
- Waves
- Reflection and Superposition
- Sound & Music
- Sound Level (Loudness)
- Doppler Effect
- Exceeding the Speed of Sound

Waves
Notes:
wave: a disturbance that travels from one place to another.”
medium: a substance that a wave travels through.
propagation: the process of a wave traveling through space.
* This is my favorite definition in these notes. I jokingly suggest that I nickname some of my students “wave” based on this definition.
mechanical wave: a wave that propagates through a medium via contact between particles of the medium. Some examples of mechanical waves include ocean waves and sound waves.
1. The energy of the wave is transmitted via the particles of the medium as the wave passes through it.
2. The wave travels through the medium. The particles of the medium are moved by the wave passing through, and then return to their original position. (The duck sitting on top of the wave below is an example.)
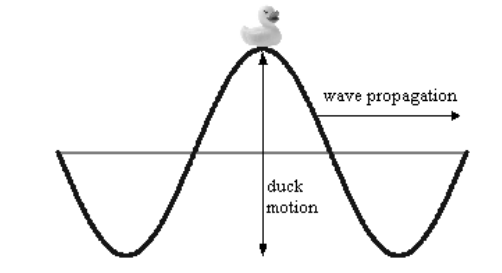
3. Waves generally move fastest in solids and slowest in liquids. The velocity of a mechanical wave is dependent on characteristics of the medium:
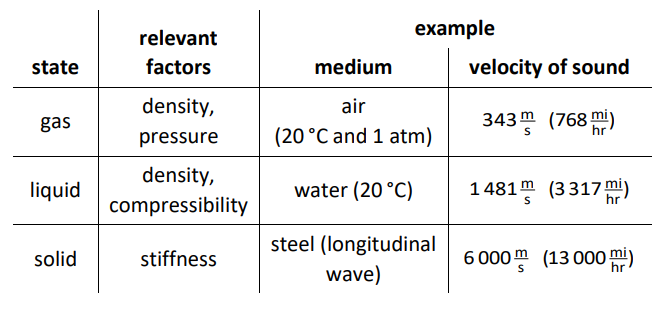
electromagnetic wave: a wave of electricity and magnetism interacting with each other. Electromagnetic waves can propagate through empty space, and are slowed down by interactions with a medium. Electromagnetic waves are discussed in more detail in the Electromagnetic Waves .
Types of Waves
transverse wave: moves its medium up \& down (or back \& forth) as it travels through. Examples: light, ocean waves
longitudinal wave (or compressional wave): compresses and decompresses the medium as it travels through. Examples: compression of a spring, sound.
torsional wave: a type of transverse wave that propagates by twisting about its direction of propagation.

The most famous example of the destructive power of a torsional wave was the Tacoma Narrows Bridge, which collapsed on November 7, 1940. On that day, strong winds caused the bridge to vibrate torsionally. At first, the edges of the bridge swayed about eighteen inches. (This behavior had been observed previously, earning the bridge the nickname “Galloping Gertie”.) However, after a support cable snapped, the vibration increased significantly, with the edges of the bridge being displaced up to 28 feet! Eventually, the bridge started twisting in two halves, one half twisting clockwise and the other half twisting counterclockwise, and then back again. This opposing torsional motion eventually caused the bridge to twist apart and collapse.

The bridge’s collapse was captured on film. Video clips of the bridge twisting and collapsing are available on the internet.
Ocean Waves
Surface Waves
surface wave: a transverse wave that travels at the interface between two mediums.Ocean waves are an example of surface waves, because they travel at the interface between the air and the water. Surface waves on the ocean are caused by wind disturbing the surface of the water. Until the wave gets to the shore, surface waves have no effect on water molecules far below the surface.
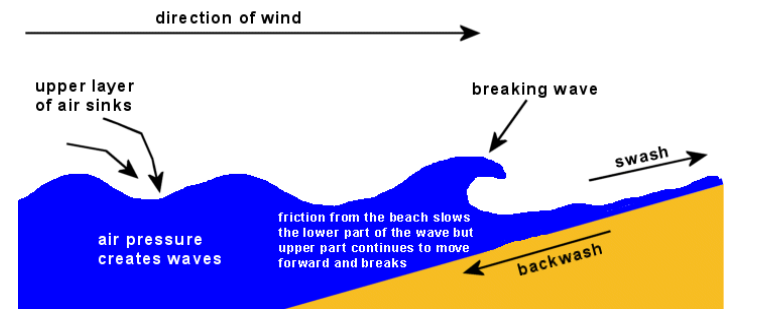
Tsunamis
The reason tsunamis are much more dangerous than regular ocean waves is because tsunamis are created by earthquakes on the ocean floor. The tsunami wave propagates through the entire depth of the water, which means tsunamis carry many times more energy than surface waves.
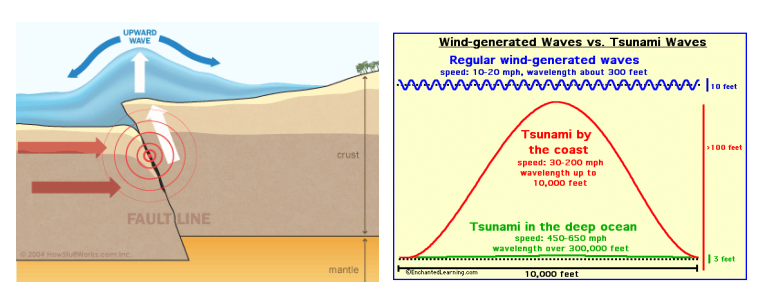
This is why a 6-12 foot high surface wave breaks harmlessly on the beach; however, a tsunami that extends 6-12 feet above the surface of the water includes a significant amount of energy throughout the entire depth of the water, and can destroy an entire city.
Properties of Waves
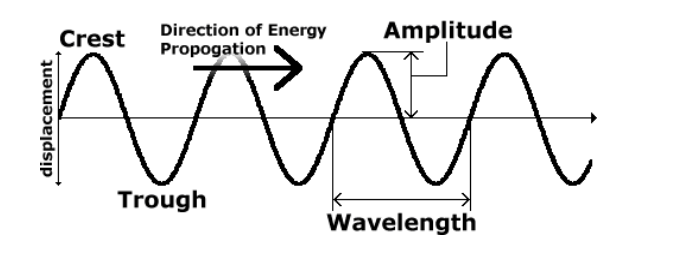
crest: the point of maximum positive displacement of a transverse wave. (The highest point.)
trough: the point of maximum negative displacement of a transverse wave. (The lowest point.)
amplitude $(A)$ : the distance of maximum displacement of a point in the medium as the wave passes through it. (The maximum height or depth.)
wavelength $(\lambda)$ : the length of the wave, measured from a specific point in the wave to the same point in the next wave. Unit $=$ distance $(\mathrm{m}, \mathrm{cm}, \mathrm{nm}$, etc. $)$
frequency $(f$ or $v)$ : the number of waves that travel past a point in a given time.
Unit $=1 /$ time $(\mathrm{Hz}=1 / \mathrm{s})$
Note that while high school physics courses generally use the variable $f$ for frequency, college courses usually use $v$ (the Greek letter “nu”, which is different from but easy to confuse with the Roman letter ” $\vee$ “).
period or time period $(T)$ : the amount of time between two adjacent waves.
Unit = time (usually seconds)
$
T=1 / f
$
velocity: the velocity of a wave depends on its frequency $(f)$ and its wavelength $(\lambda)$ :
$
v=\lambda f
$
The velocity of electromagnetic waves (such as light, radio waves, microwaves, X-rays, etc.) is called the speed of light, which is $3.00 \times 10^8 \frac{\mathrm{m}}{\mathrm{s}}$ in a vacuum. The speed of light is slower in a medium that has an index of refraction ${ }^*$ greater than 1.
The velocity of a wave traveling through a string under tension (such as a piece of string, a rubber band, a violin/guitar string, etc.) depends on the tension and the ratio of the mass of the string to its length:
$
v_{\text {string }}=\sqrt{\frac{F_T L}{m}}
$
where $F_T$ is the tension in the string, $L$ is the length, and $m$ is the mass.
Sample Problem:
Q: The Boston radio station WZLX broadcasts waves with a frequency of 100.7 $\mathrm{MHz}$. If the waves travel at the speed of light, what is the wavelength?
Answer/Explanation
A: $f=100.7 \mathrm{MHz}=100700000 \mathrm{~Hz}=1.007 \times 10^8 \mathrm{~Hz}$
$
v=c=3.00 \times 10^8 \frac{\mathrm{m}}{\mathrm{s}}
$
$
\begin{aligned}
& v=\lambda f \\
& 3.00 \times 10^8=\lambda\left(1.007 \times 10^8\right) \\
& \lambda=\frac{3.00 \times 10^8}{1.007 \times 10^8}=2.98 \mathrm{~m}
\end{aligned}
$
The index of refraction is a measure of how much light bends when it moves between one medium and another. The sine of the angle of refraction is proportional to the speed of light in that medium. Index of refraction is studied as part of optics in Physics 2.
Reflection and Superposition
Notes:
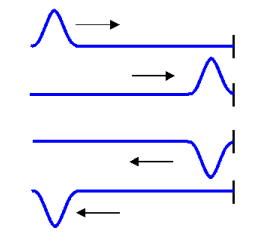
Reflection of Waves
reflection: when a wave hits a fixed (stationary) point and “bounces” back.
Notice that when the end of the rope is fixed, the reflected wave is inverted. (If the end of the rope were free, the wave would not invert.)
Superposition of Waves
When waves are superimposed (occupy the same space), their amplitudes add.
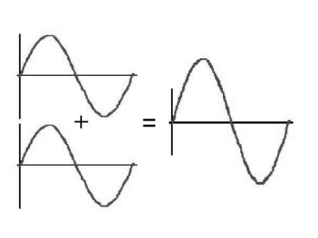
constructive interference: when waves add in a way that the amplitude of the resulting wave is larger than the amplitudes of the component waves.
Because the wavelengths are the same and the maximum, minimum, and zero points all coïncide (line up), the two component waves are said to be “in phase” with each other.
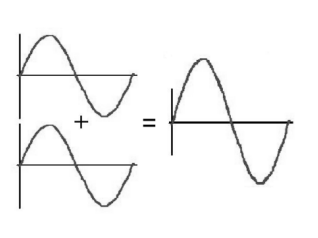
destructive interference: when waves add in a way that the amplitude of the resulting wave is smaller than the amplitudes of the component waves. (Sometimes we say that the waves “cancel” each other.)
Because the wavelengths are the same but the maximum, minimum, and zero points do not coïncide, the waves are said to be “out of phase” with each other.
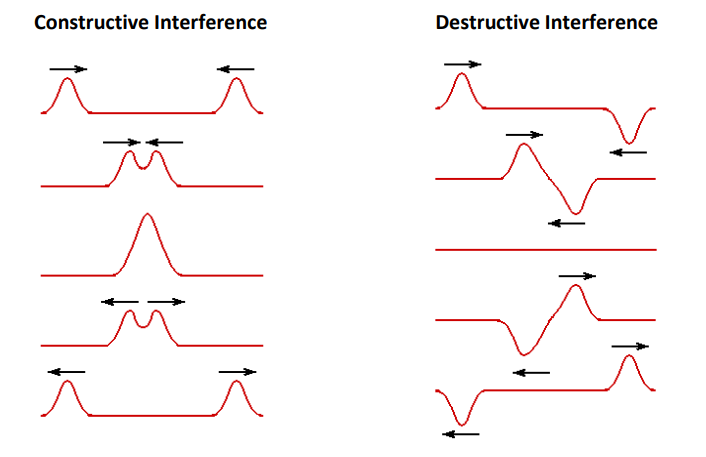
Note that waves can travel in two opposing directions at the same time. When this happens, the waves pass through each other, exhibiting constructive and/or destructive interference as they pass:
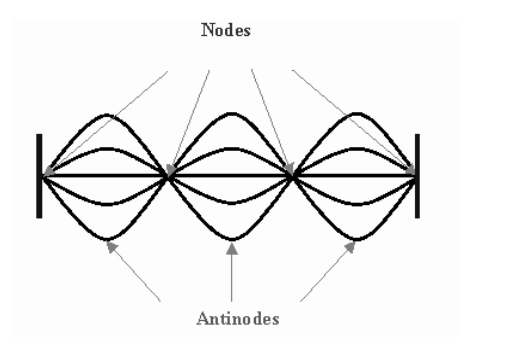
Standing Waves
standing wave: when half of the wavelength is an exact fraction of the length of a medium that is vibrating, the wave reflects back and the reflected wave interferes constructively with itself. This causes the wave to appear stationary.
Points along the wave that are not moving are called “nodes”. Points of maximum displacement are called “antinodes”.
When we add waves with different wavelengths and amplitudes, the result can be complex:
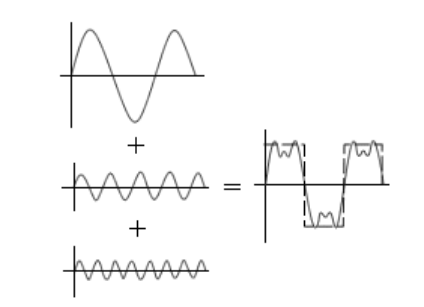
This is how radio waves encode a signal on top of a “carrier” wave. Your radio’s antenna receives (“picks up”) radio waves within a certain range of frequencies. Imagine that the bottom wave (the one with the shortest wavelength and highest frequency) is the “carrier” wave. If you tune your radio to its frequency, the radio will filter out other waves that don’t include the carrier frequency. Then your radio subtracts the carrier wave, and everything that is left is sent to the speakers.
Two-Dimensional Interference Patterns
When two progressive waves propagate into each other’s space, the waves produce interference patterns. This diagram shows how interference patterns form:
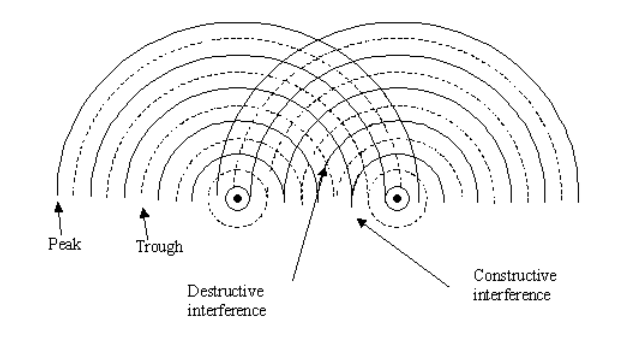
The resulting interference pattern looks like the following picture:

In this picture, the bright regions are wave peaks, and the dark regions are troughs. The brightest intersections are regions where the peaks interfere constructively, and the darkest intersections are regions where the troughs interfere constructively.
The following picture ${ }^*$ shows an interference pattern created by ocean waves, one of which has been reflected off a point on the shore. The wave at the left side of the picture is traveling toward the right, and the reflected wave at the bottom right of the picture is traveling toward the top of the picture.
Because the sun is low in the sky (the picture was taken just before sunset), the light is reflected off the water, and the crests of the waves produce shadows behind them.

${ }^*$ The picture is taken from Tortola in the British Virgin Islands, looking west toward Jost Van Dyke.
Sound & Music
Notes:
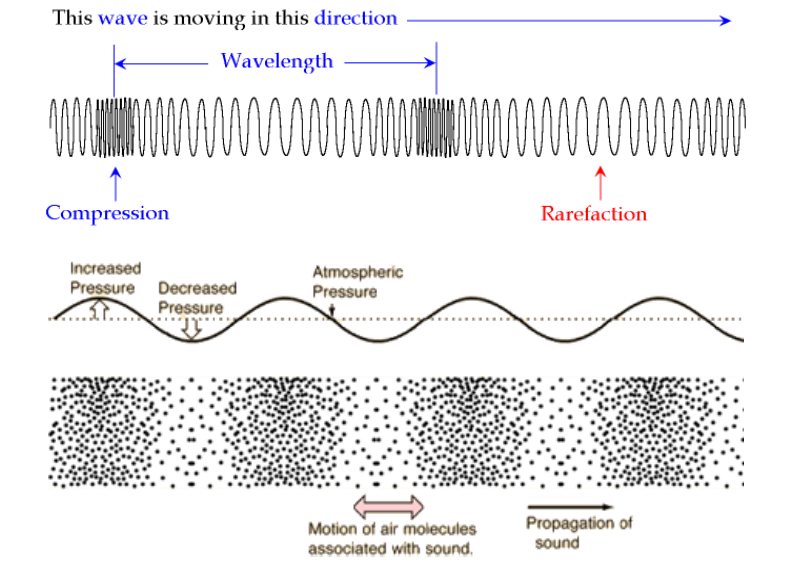
Sound waves are caused by vibrations that create longitudinal (compressional) waves in the medium they travel through (such as air).
pitch: how “high” or “low” a musical note is. The pitch is determined by the frequency of the sound wave.

resonance: when the wavelength of a half-wave (or an integer number of halfwaves) coincides with one of the dimensions of an object. This creates standing waves that reinforce and amplify each other. The body of a musical instrument is an example of an object that is designed to use resonance to amplify the sounds that the instrument produces.
String Instruments
A string instrument (such as a violin or guitar) typically has four or more strings. The lower strings (strings that sound with lower pitches) are thicker, and higher strings are thinner. Pegs are used to tune the instrument by increasing (tightening) or decreasing (loosening) the tension on each string.
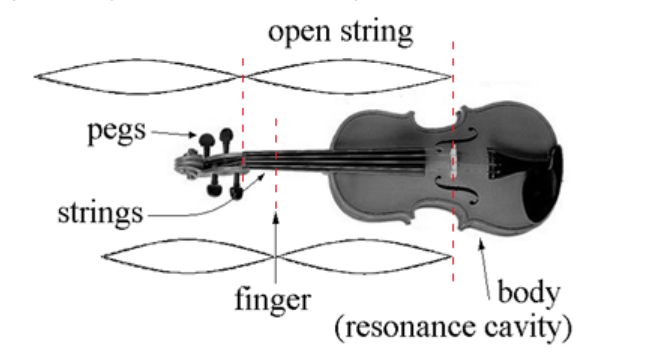
The vibration of the string creates a half-wave, i.e., $\lambda=2 \mathrm{~L}$. The musician changes the half-wavelength by using a finger to shorten the part of the string that vibrates. (A shorter wavelength produces a higher frequency $=$ higher pitch.)
The velocity of the wave produced on a string depends on the tension and the length and mass of the vibrating portion. The velocity is given by the equation:
$
v_{\text {string }}=\sqrt{\frac{F_T L}{m}}
$
Where: $
\begin{array}{ll}
f=\text { frequency }(\mathrm{Hz}) & F_T=\operatorname{tension}(\mathrm{N}) \\
m=\text { mass of string }(\mathrm{kg}) & L=\text { length of string }(\mathrm{m})=\frac{\lambda}{2}
\end{array}
$
Given the velocity and wavelength, the frequency (pitch) is therefore:
$
f=\frac{v}{\lambda}=\frac{v}{2 L}=\frac{1}{2 L} \sqrt{\frac{F_T L}{m}}=\sqrt{\frac{F_T}{4 m L}}
$
Pipes and Wind Instruments
A pipe (in the musical instrument sense) is a tube filled with air. The design of the mouthpiece (or air inlet) causes the air to oscillate as it enters the pipe. This causes the air molecules to compress and spread out at regular intervals based on the dimensions of the closed section of the instrument, which determines the wavelength. The wavelength and speed of sound determine the frequency.
Most wind instruments use one of three ways of causing the air to oscillate:
Brass Instruments
With brass instruments like trumpets, trombones, French horns, etc., the player presses his/her lips tightly against the mouthpiece, and the player’s lips vibrate at the appropriate frequency.
Reed Instruments
With reed instruments, air is blown past a reed (a semi-stiff object) that vibrates back and forth. Clarinets and saxophones use a single reed made from a piece of cane (a semi-stiff plant similar to bamboo). Oboes and bassoons (“double-reed instruments”) use two pieces of cane that vibrate against each other. Harmonicas and accordions use reeds made from a thin piece of metal.
Whistles (Instruments with Fipples)
Instruments with fipples include recorders, whistles and flutes. A fipple is a sharp edge that air is blown past. The separation of the air going past the fipple results in a pressure difference on one side vs. the other. Air moves toward the lower pressure side, causing air to build up and the pressure to increase. When the pressure becomes greater than the other side, the air switches abruptly to the other side of the fipple. Then the pressure builds on the other side until the air switches back:

The frequency of this back-and-forth motion is what determines the pitch.
Open vs. Closed-Pipe Instruments
An open-pipe instrument has an opening at each end. A closed-pipe instrument has an opening at one end, and is closed at the other.
Examples of open-pipe instruments include uncapped organ pipes, whistles, recorders and flutes.
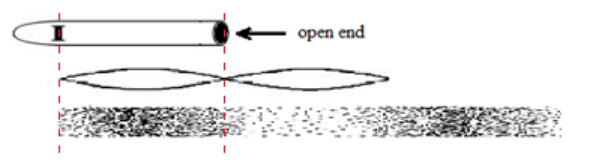
Notice that the two openings determine where the air pressure must be equal to atmospheric pressure (i.e., the air is neither compressed nor expanded). This means that the length of the body of the instrument $(L)$ is a half-wave, and that the wavelength $(\lambda)$ of the sound produced must therefore be twice as long, i.e., $\lambda=2 L$. (This is similar to string instruments, in which the length of the vibrating string is a half-wave.)
Examples of closed-pipe instruments include clarinets and all brass instruments. Air is blown in at high pressure via the mouthpiece, which means the mouthpiece is an antinode-a region of maximum displacement of the individual air molecules. This means that the body of the instrument is the distance from the antinode to a region of atmospheric pressure, i.e., one-fourth of a wave. This means that for closed-pipe instruments, $\lambda=4 L$.
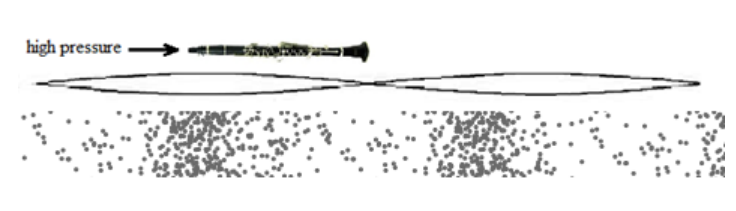
The difference in the resonant wavelength $(4 L v s .2 L)$ is why a closed-pipe instrument (e.g., a clarinet) sounds an octave lower than an open-pipe instrument of similar length (e.g., a flute)-twice the wavelength results in half the frequency.
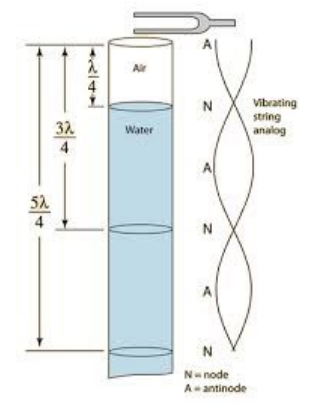
The principle of a closed-pipe instrument can be used in a lab experiment to determine the frequency of a tuning fork (or the speed of sound) using a resonance tube-an open tube filled with water to a specific depth.
A tuning fork generates an oscillation of a precise frequency at the top of the tube. Because this is a closed pipe, the source (just above the tube) is an antinode (maximum amplitude).
When the height of air above the water is exactly $1 / 4$ of a wavelength $\left(\frac{\lambda}{4}\right)$, the waves that are reflected back have maximum constructive interference with the source wave, which causes the sound to be significantly amplified. This phenomenon is called resonance.
Resonance will occur at every antinode-i.e., any integer plus $1 / 4$ of a wave
$
\left(\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4} \text {, etc. }\right)
$
Open vs. Closed-Pipe Instruments
An open-pipe instrument has an opening at each end. A closed-pipe instrument has an opening at one end, and is closed at the other.
Examples of open-pipe instruments include uncapped organ pipes, whistles, recorders and flutes.

Notice that the two openings determine where the air pressure must be equal to atmospheric pressure (i.e., the air is neither compressed nor expanded). This means that the length of the body of the instrument $(L)$ is a half-wave, and that the wavelength $(\lambda)$ of the sound produced must therefore be twice as long, i.e., $\lambda=2 L$. (This is similar to string instruments, in which the length of the vibrating string is a half-wave.)
Examples of closed-pipe instruments include clarinets and all brass instruments. Air is blown in at high pressure via the mouthpiece, which means the mouthpiece is an antinode-a region of maximum displacement of the individual air molecules. This means that the body of the instrument is the distance from the antinode to a region of atmospheric pressure, i.e., one-fourth of a wave. This means that for closed-pipe instruments, $\lambda=4 L$.

The difference in the resonant wavelength $(4 L v s .2 L)$ is why a closed-pipe instrument (e.g., a clarinet) sounds an octave lower than an open-pipe instrument of similar length (e.g., a flute)-twice the wavelength results in half the frequency.

The principle of a closed-pipe instrument can be used in a lab experiment to determine the frequency of a tuning fork (or the speed of sound) using a resonance tube-an open tube filled with water to a specific depth.
A tuning fork generates an oscillation of a precise frequency at the top of the tube. Because this is a closed pipe, the source (just above the tube) is an antinode (maximum amplitude).
When the height of air above the water is exactly $1 / 4$ of a wavelength $\left(\frac{\lambda}{4}\right)$, the waves that are reflected back have maximum constructive interference with the source wave, which causes the sound to be significantly amplified. This phenomenon is called resonance.
Resonance will occur at every antinode-i.e., any integer plus $1 / 4$ of a wave
$
\left(\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4} \text {, etc. }\right)
$
Playing Different Pitches (Frequencies)
For an instrument with holes, like a flute or recorder, the first open hole is the first place in the pipe where the pressure is equal to atmospheric pressure, which determines the half-wavelength (or quarter-wavelength):

The speed of sound in air is $v_s\left(343 \frac{\mathrm{m}}{\mathrm{s}}\right.$ at $20^{\circ} \mathrm{C}$ and 1 atm), which means the frequency of the note (from the formula $v_s=\lambda f$ ) will be:
$f=\frac{v_s}{2 L}$ for an open-pipe instrument (e.g., flute, recorder, whistle)
$f=\frac{V_s}{4 L}$ for an closed-pipe instrument (e.g., clarinet, brass instrument).
Note that the frequency is directly proportional to the speed of sound in air. The speed of sound increases as the temperature increases, which means that as the air gets colder, the frequency gets lower, and as the air gets warmer, the frequency gets higher. This is why wind instruments go flat at colder temperatures and sharp at warmer temperatures. Musicians claim that the instrument is going out of tune, but actually it’s not the instrument that is out of tune, but the speed of sound!
Note however, that the frequency is inversely proportional to the wavelength (which depends largely on the length of the instrument). This means that the extent to which the frequency changes with temperature will be different for different-sized instruments, which means the band will become more and more out of tune with itself as the temperature changes.
Helmholtz Resonators
The resonant frequency of a bottle or similar container (called a Helmholtz resonator, named after the German physicist Hermann von Helmholtz) is more complicated to calculate.
For an enclosed volume of air with a single opening, the resonant frequency depends on the resonant frequency of the air in the large cavity, and the crosssectional area of the opening.

For a bottle with a neck, the air in the neck behaves like a spring, with a spring constant that is proportional to the volume of air in the neck:

where: $
\begin{aligned}
& f=\text { resonant frequency } \\
& v_{\mathrm{s}}=\text { speed of sound in air }\left(343 \frac{\mathrm{m}}{\mathrm{s}} \text { at } 20{ }^{\circ} \mathrm{C} \text { and } 1 \text { atm }\right) \\
& A=\text { cross-sectional area of the neck of the bottle }\left(\mathrm{m}^2\right) \\
& V_0=\text { volume of the main cavity of the bottle }\left(\mathrm{m}^3\right) \\
& L=\text { length of the neck of the bottle }(\mathrm{m})
\end{aligned}
$
(Note that it may be more convenient to use measurements in $\mathrm{cm}, \mathrm{cm}^2$, and $\mathrm{cm}^3$, and use $v_s=34300 \frac{\mathrm{cm}}{\mathrm{s}}$.)
Blowing across the top of an open bottle is an example of a Helmholtz resonator.
You can make your mouth into a Helmholtz resonator by tapping on your cheek with your mouth open. You can change the pitch by opening or closing your mouth a little, which changes the area of the opening $(A)$.
Frequencies of Music Notes
The frequencies that correspond with the pitches of the Western equal temperament scale are:
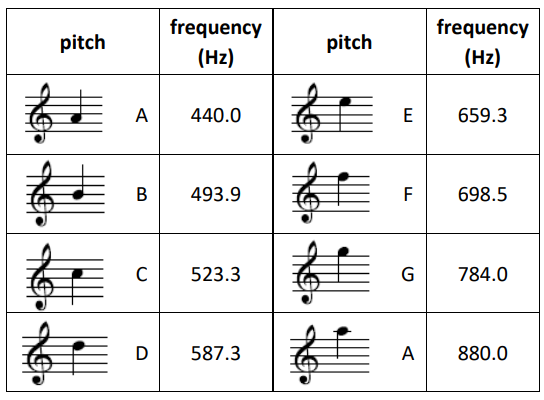
A note that is an octave above another note has exactly twice the frequency of the lower note. For example, the $A$ in on the second line of the treble clef staff has a frequency of $440 \mathrm{~Hz}$. The $A$ an octave above it (one ledger line above the staff) has a frequency of $440 \times 2=880 \mathrm{~Hz}$
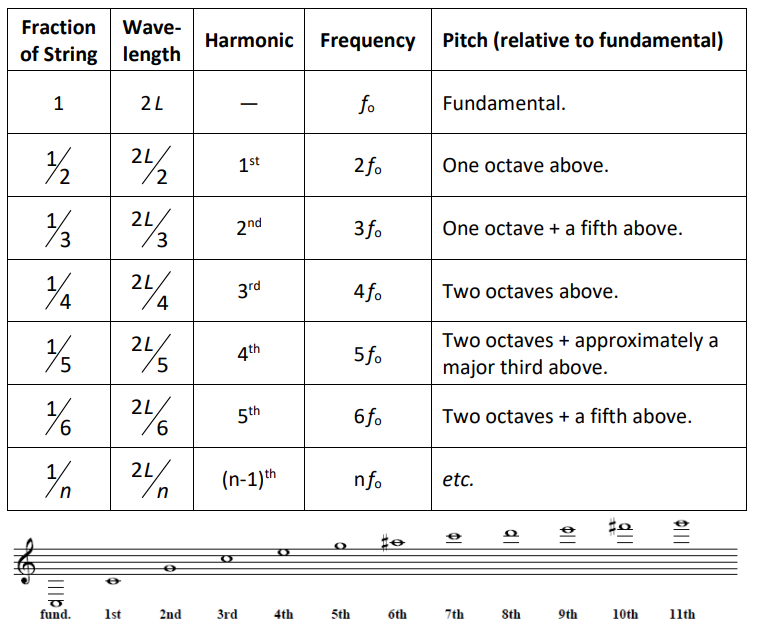
Harmonic Series
harmonic series: the additional, shorter standing waves that are generated by a vibrating string or column of air that correspond with integer numbers of halfwaves.
fundamental frequency: the natural resonant frequency of a particular pitch.
harmonic: a resonant frequency produced by vibrations that contain an integer number of half-waves that add up to the half-wavelength of the fundamental.
The harmonics are numbered based on their pitch relative to the fundamental frequency. The harmonic that is closest in pitch is the $1^{\text {st }}$ harmonic, the next closest is the $2^{\text {nd }}$ harmonic, etc.
Any sound wave that is produced in a resonance chamber (such as a musical instrument) will produce the fundamental frequency plus all of the other waves of the harmonic series. The fundamental is the loudest, and each harmonic gets more quiet as you go up the harmonic series.
” Most bands and orchestras define the note ” $\mathrm{A}$ ” to be exactly $440 \mathrm{~Hz}$, and use it for tuning.
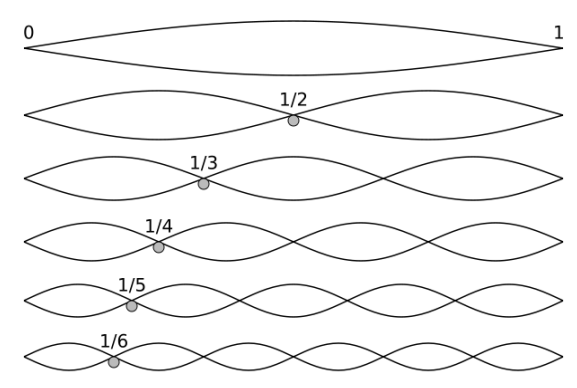
The following diagram shows the waves of the fundamental frequency and the first five harmonics in a pipe or a vibrating string:
Beats
When two or more waves are close but not identical in frequency, their amplitudes reinforce each other at regular intervals.
For example, when the following pair of waves travels through the same medium, the amplitudes of the two waves have maximum constructive interference every five half-waves ( $21 \frac{1}{2}$ full waves) of the top wave and every six half-waves ( 3 full waves) of the bottom wave.

If this happens with sound waves, you will hear a pulse or “beat” every time the two maxima coïncide.
The closer the two wavelengths (and therefore also the two frequencies) are to each other, the more half-waves it takes before the amplitudes coïncide. This means that as the frequencies get closer, the time between beats gets longer.
Piano tuners listen for these beats, and adjust the tension of the string they are tuning until the time between beats gets longer and longer and finally disappears.
The Biophysics of Sound
When a person speaks, abdominal muscles force air from the lungs through the larynx.
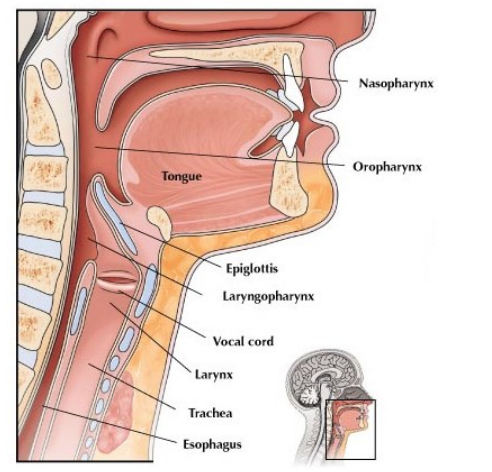
The vocal cord vibrates, and this vibration creates sound waves. Muscles tighten or loosen the vocal cord, which changes the frequency at which it vibrates. Just like in a string instrument, the change in tension changes the pitch. Tightening the vocal cord increases the tension and produces a higher pitch, and relaxing the vocal cord decreases the tension and produces a lower pitch.
This process happens when you sing. Amateur musicians who sing a lot of high notes can develop laryngitis from tightening their laryngeal muscles too much for too long. Professional musicians need to train themselves to keep their larynx muscles relaxed and use other techniques (such as air pressure, which comes from breath support via the abdominal muscles) to adjust their pitch.
When the sound reaches the ears, it travels through the auditory canal and causes the tympanic membrane (eardrum) to vibrate. The vibrations of the tympanic membrane cause pressure waves to travel through the middle ear and through the oval window into the cochlea.
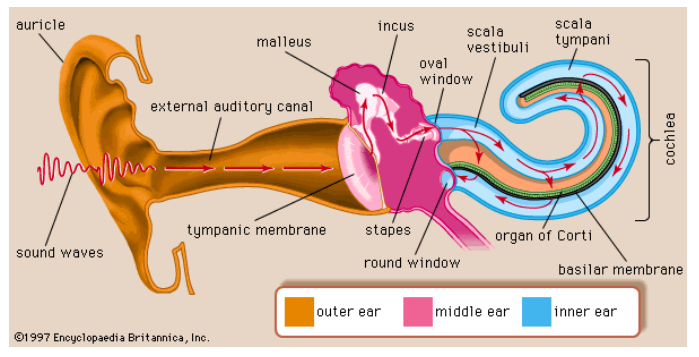
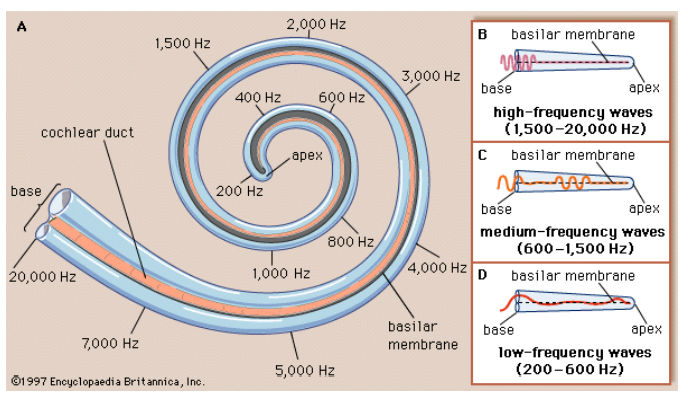
The basilar membrane in the cochlea is a membrane with cilia (small hairs) connected to it, which can detect very small movements of the membrane. As with a resonance tube, the wavelength determines exactly where the sound waves will vibrate the basilar membrane the most strongly, and the brain determines the pitch (frequency) of a sound based on the precise locations excited by these frequencies.
Sound Level (Loudness)
Notes:
sound level: the perceived intensity of a sound. Usually called “volume”.
Sound level is usually measured in decibels (dB). One decibel is one tenth of one bel.
Sound level is calculated based on the logarithm of the ratio of the power (energy per unit time) causing a sound vibration to the power that causes some reference sound level.
You will not be asked to calculate decibels from an equation, but you should understand that because the scale is logarithmic, a difference of one bel $(10 \mathrm{~dB})$ represents a tenfold increase or decrease in sound level.
Doppler Effect
Notes:
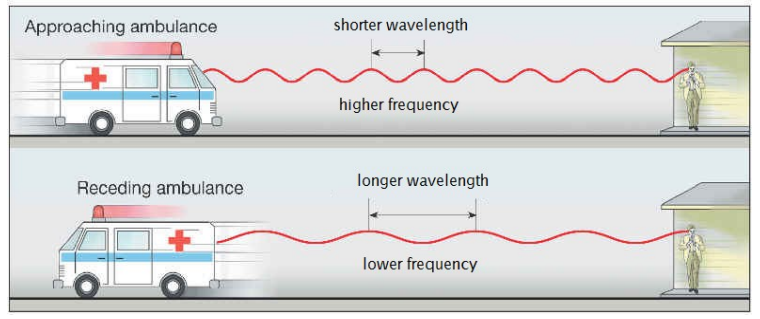
Doppler effect or Doppler shift: the apparent change in frequency/wavelength of a wave due to a difference in velocity between the source of the wave and the observer. The effect is named for the Austrian physicist Christian Doppler.
You have probably noticed the Doppler effect when an emergency vehicle with a siren drives by.

Why the Doppler Shift Happens
The Doppler shift occurs because a wave is created by a series of pulses at regular intervals, and the wave moves at a particular speed.
If the source is approaching, each pulse arrives sooner than it would have if the source had been stationary. Because frequency is the number of pulses that arrive in one second, the moving source results in an increase in the frequency observed by the receiver.
Similarly, if the source is moving away from the observer, each pulse arrives later, and the observed frequency is lower.
Calculating the Doppler Shift
The change in frequency is given by the equation:
$
f=f_o\left(\frac{v_w \pm v_r}{v_w \pm v_s}\right)
$
where:
$
\begin{aligned}
& f=\text { observed frequency } \\
& f_0=\text { frequency of the original wave } \\
& v_w=\text { velocity of the wave } \\
& v_r=\text { velocity of the receiver (you) } \\
& v_s=\text { velocity of the source }
\end{aligned}
$
The rule for adding or subtracting velocities is:
•The receiver’s (your) velocity is in the numerator. If you are moving toward the sound, this makes the pulses arrive sooner, which makes the frequency higher. So if you are moving toward the sound, add your velocity. If you are moving away from the sound, subtract your velocity.
• The source’s velocity is in the denominator. If the source is moving toward you, this makes the frequency higher, which means the denominator needs to be smaller. This means that if the source is moving toward you, subtract its velocity. If the source is moving away from you, add its velocity.
Don’t try to memorize a rule for this-you will just confuse yourself. It’s safer to reason through the equation. If something that’s moving would make the frequency higher, that means you need to make the numerator larger or the denominator smaller. If it would make the frequency lower, that means you need to make the numerator smaller or the denominator larger.
Sample Problem:
Q: The horn on a fire truck sounds at a pitch of $350 \mathrm{~Hz}$. What is the perceived frequency when the fire truck is moving toward you at $20 \frac{\mathrm{m}}{\mathrm{s}}$ ? What is the perceived frequency when the fire truck is moving away from you at $20 \frac{\mathrm{m}}{\mathrm{s}}$ ?
Assume the speed of sound in air is $343 \frac{\mathrm{m}}{\mathrm{s}}$.
Answer/Explanation
A: The observer is not moving, so $v_{\mathrm{r}}=0$.
The fire truck is the source, so its velocity appears in the denominator.
When the fire truck is moving toward you, that makes the frequency higher. This means we need to make the denominator smaller, which means we need to subtract $v_{\mathrm{s}}$ :
$
f=f_o\left(\frac{v_w}{v_w-v_s}\right)=350\left(\frac{343}{343-20}\right)=350(1.062)=372 \mathrm{~Hz}
$
When the fire truck is moving away, the frequency will be lower, which mean we need to make the denominator larger. This means we need to add $v_{\mathrm{s}}$ :
$
f=f_o\left(\frac{v_w}{v_w+v_s}\right)=350\left(\frac{343}{343+20}\right)=350(0.9449)=331 \mathrm{~Hz}
$
Note that the pitch shift in each direction corresponds with about one half-step on the musical scale.
Exceeding the Speed of Sound
Notes:
The speed of an object relative to the speed of sound in the same medium is called the Mach number (abbreviation Ma), named after the Austrian physicist Ernst Mach.
$
M a=\frac{v_{\text {object }}}{v_{\text {sound }}}
$
Thus “Mach 1 ” or a speed of $\mathrm{Ma}=1$ is the speed of sound. An object such as an airplane that is moving at 1.5 times the speed of sound would be traveling at “Mach $1.5^{\prime \prime}$ or $\mathrm{Ma}=1.5$.
When an object such as an airplane is traveling slower than the speed of sound $(\mathrm{Ma}<1)$, the jet engine noise is Doppler shifted just like any other sound wave. When the airplane’s velocity reaches the speed of sound $(\mathrm{Ma}=1)$, the leading edge of all of the sound waves produced by the plane coincides. These waves amplify each other, producing a loud shock wave called a “sonic boom”.
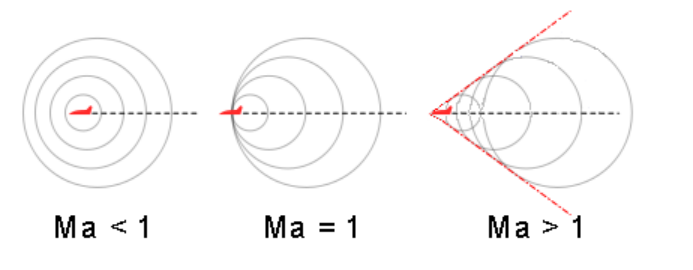
When an airplane is traveling faster than sound, the sound waves coincide at points behind the airplane at a specific angle, $\alpha$ :
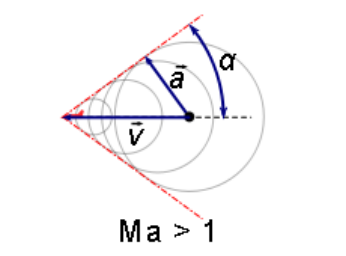
The angle $\alpha$ is given by the equation:
$
\sin (\alpha)=\frac{1}{M a}
$
Note that the airplane cannot be heard at points outside of the region defined by the angle $\alpha$. Note also that the faster the airplane is traveling, the smaller the angle $\alpha$, and the narrower the cone.
The shock wave temporarily increases the temperature of the air affected by it. If the air is humid enough, when it cools by returning to its normal pressure, the water vapor condenses and forms a cloud, called a vapor cone:

The “crack” of a bullwhip is also a sonic boom-when a bullwhip is snapped sharply, the end of the bullwhip travels faster than sound and creates a miniature shock wave.