Topics covered in this chapter:
Photoelectric Effect
Notes:
The photoelectric effect was discovered in 1887 when Heinrich Hertz discovered that electrodes emitted sparks more effectively when ultraviolet light was shone on them. We now know that the particles are electrons, and that ultraviolet light of sufficiently high frequency (which varies from element to element) causes the electrons to be emitted from the surface of the element:
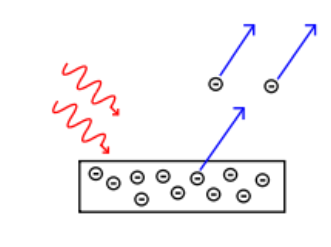
The photoelectric effect requires light with a sufficiently high frequency, because the frequency of the light is related to the amount of energy it carries. The energy of the photons needs to be above a certain threshold frequency in order to have enough energy to ionize the atom.
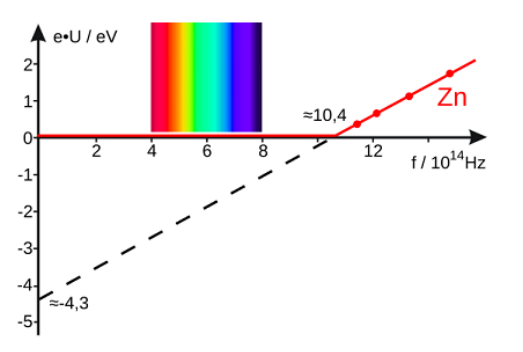
For example, a minimum frequency of $10.4 \times 10^{14} \mathrm{~Hz}$ is needed to dislodge electrons from a zinc atom:
The maximum kinetic energy of the emitted electron is equal to Planck’s constant times the difference between the frequency of incident light $(f)$ and the minimum threshold frequency of the element $\left(f_0\right)$ :
$
K_{\max }=h\left(f-f_o\right)
$
The quantity $h f_0$ is called the “work function” of the atom, and is denoted by the variable $\phi$. Thus the kinetic energy equation can be rewritten as:
$
K_{\max }=h f-\phi
$
Values of the work function for different elements range from about $2.3-6 \mathrm{eV}$.
$
\left(1 \mathrm{eV}=1.6 \times 10^{-19} \mathrm{~J}\right)
$
The importance of this discovery was that it gave rise to the idea that light can behave both as a wave and as a particle.
In 1905, Albert Einstein published a paper explaining that the photoelectric effect was evidence that energy from light was carried in discrete, quantized packets. This discovery, for which Einstein was awarded the Nobel prize in physics in 1921, led to the birth of the field of quantum physics.
Bohr Model of the Hydrogen Atom
Notes:
Significant Developments Prior to 1913
Discovery of the Electron (1897): English physicist J.J. Thomson determined that cathode rays were actually particles emitted from atoms that the cathode was made of. These particles had an electrical charge, so they were named “electrons” (though Thomson called them “corpuscles”).
Discovery of the Atomic Nucleus (1909): English physicist Ernest Rutherford’s famous “gold foil experiment” determined that atoms contained a dense, positively-charged region that comprised most of the atom’s mass. This region was named the “nucleus”, after the nucleus of a cell.
“Planetary” Model of the Atom (early 1900s): The atom was believed to be like a miniature solar system, with electrons orbiting the nucleus in much the same way as planets orbit the sun. The model is often attributed to Rutherford in 1911 (following his gold foil experiment), but the existence of the nucleus and the planetary model were described several years earlier, notably in a high school physics textbook ${ }^*$ in 1906.
Spectroscopy
Balmer Formula (1885): Johann Balmer devised an empirical equation to relate the emission lines in the visible spectrum for the hydrogen atom.
Rydberg Formula (1888): Johannes Rydberg developed a generalized formula that could describe the wave numbers of all of the spectral lines in hydrogen (and similar elements).
There are several series of spectral lines for hydrogen, each of which converge at different wavelengths. Rydberg described the Balmer series in terms of a pair of integers $\left(n_1\right.$ and $n_2$, where $\left.n_1<n_2\right)$, and devised a single formula with a single constant (now called the Rydberg constant) that relates them.
$
\frac{1}{\lambda_{\text {vac }}}=R_H\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)
$
The value of Rydberg’s constant is $\frac{m_e e^4}{8 \varepsilon_o^2 h^3 c}=10973731.6 \mathrm{~m}^{-1} \approx 1.1 \times 10^7 \mathrm{~m}^{-1}$ where $m_e$ is the rest mass of the electron, $e$ is the elementary charge, $\varepsilon_o$ is the permittivity of free space, $h$ is Planck’s constant, and $c$ is the speed of light in a vacuum.
Rydberg’s equation was later found to be consistent with other series discovered later, including the Lyman series (in the ultraviolet region; first discovered in 1906) and the Paschen series (in the infrared region; first discovered in 1908).
Those series and their converging wavelengths are:
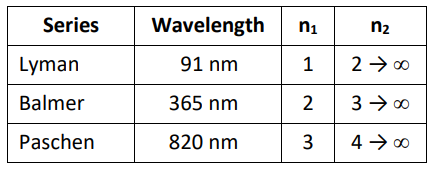
* Robert A. Millikan and Henry Gale. First Course in Physics. Ginn & Company, 1906, pp. 473-474.
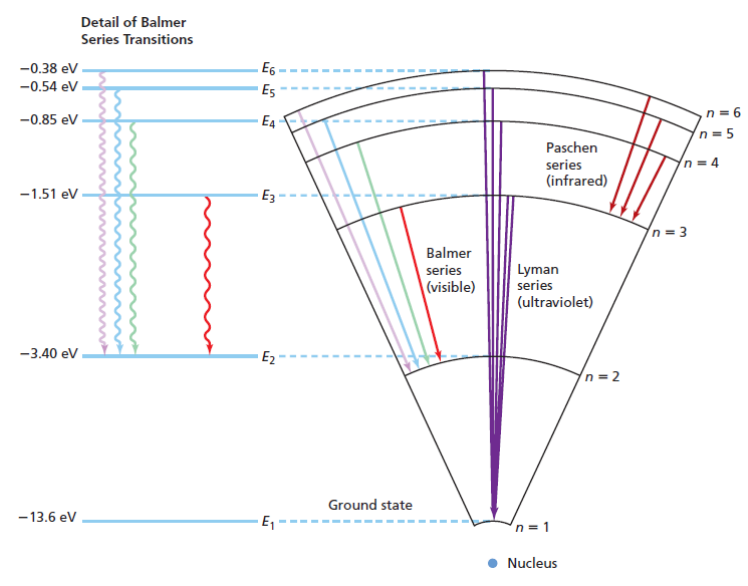
The following diagram shows Lyman, Balmer and Paschen series transitions form higher energy levels (n = 2 through n = 6) back to lower ones (n = 1 through n = 3):
Early Quantum Theory
quantum: an elementary unit of energy.
In 1900, German physicist Max Planck published the Planck postulate, stating that electromagnetic energy could be emitted only in quantized form, i.e., only certain “allowed” energy states are possible.
Plack determined the constant that bears his name as the relationship between the frequency of one quantum unit of electromagnetic wave and its energy. This relationship is the equation:
$
E=h f
$
where:
$
\begin{aligned}
& E=\text { energy }(\mathrm{J}) \\
& h=\text { Planck’s constant }=6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s} \\
& f=\text { frequency }\left(\mathrm{Hz} \equiv^{-1}\right)
\end{aligned}
$
* Most physics texts use the Greek letter $v(\mathrm{nu})$ as the variable for frequency. However, high school texts and the College Board use $f$, presumably to avoid confusion with the letter ” $v “$.
Bohr’s Model of the Atom (1913)
In 1913, Niels Bohr combined atomic, quantum and spectroscopy theories into a single unified theory. Bohr hypothesized that electrons moved around the nucleus as in Rutherford’s model, but that these electrons had only certain allowed quantum values of energy, which could be described by a quantum number $(n)$. The value of that quantum number was the same $n$ as in Rydberg’s equation, and that using quantum numbers in Rydberg’s equation could predict the wavelengths of light emitted when the electrons gained or lost energy by moved from one quantum level to another.
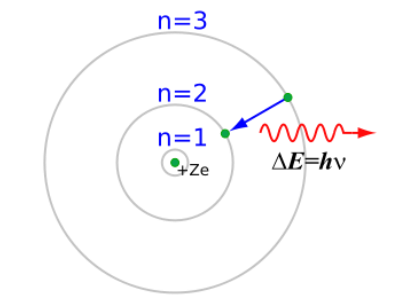
Bohr’s model gained wide acceptance, because it related several prominent theories of the time.
The theory worked well for hydrogen, giving a theoretical basis for Rydberg’s equation. Bohr defined the energy associated with a quantum number $(n)$ in terms of Rydberg’s constant:
$
E_n=-\frac{R_H}{n^2}
$
Although the Bohr model worked well for hydrogen, the equations could not be solved exactly for atoms with more than one electron, because of the additional effects that electrons exert on each other (e.g., the Coulomb force, $F_e=\frac{1}{4 \pi \varepsilon_o} \frac{q_1 q_2}{r^2}$
Wave-Particle Duality
Notes:
In 1924, French physicist Louis de Broglie determined that quanta of light could be considered to particles with very small mass moving at relativistic speeds (i.e., close to the speed of light. See the section on Introduction: Special Relativity starting on page 547.)
From this, de Broglie concluded that any moving particle or object must therefore be able to be characterized with some periodic frequency, $f=\frac{E}{h}$, from Planck’s equation. This means that the wavelength of any moving object is therefore:
$
\lambda=\frac{h}{p}=\frac{h}{m v}
$
where:
$
\begin{aligned}
\lambda & =\text { de Broglie wavelength }(\mathrm{m}) \\
h & =\text { Planck’s constant }=6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s} \\
p & =\text { momentum }(\mathrm{N} \cdot \mathrm{s}) \\
m & =\operatorname{mass}(\mathrm{kg}) \\
v & =\text { velocity }\left(\frac{\mathrm{m}}{\mathrm{s}}\right)
\end{aligned}
$
Every moving object has a de Broglie wavelength, though wavelengths of large objects are too small to be detectable.
de Broglie theorized that if waves were considered to be electrons, then the reason that only certain wavelengths were possible was because the wave produced by an electron would only be stable if the path length as it orbited the nucleus was an integer multiple of the wavelength.
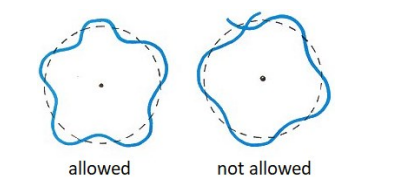
Different quantum amounts of energy were possible with de Broglie’s theory, but were restricted to amounts that produced an integer number of wavelengths.
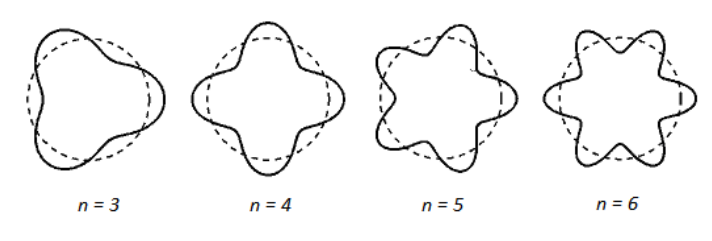
Quantum Mechanical Model of the Atom
Notes:
In 1925, following de Broglie’s research, Austrian physicist Erwin Schrödinger found that by treating each electron as a unique wave function, the energies of the electrons could be predicted by the mathematical solutions to the wave equation*. Schrödinger used the wave equation to construct a probability map for where the electrons can be found in an atom. Schrödinger’s work is the basis for the modern quantum-mechanical model of the atom.
* The wave equation in physics is a second-order partial differential equation that mathematically describes the behavior of waves in space and time. The mathematics required are well beyond the scope of a high school physics class.
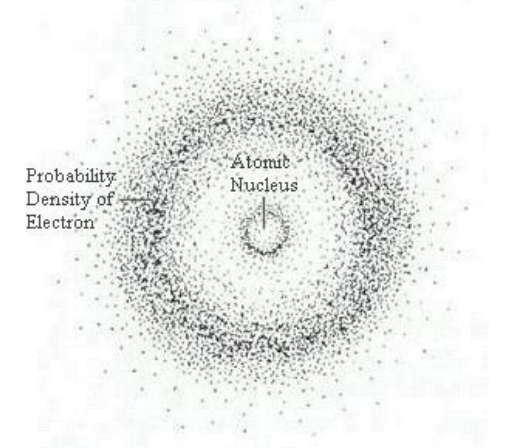
To understand the probability map, it is important to realize that because the electron acts as a wave, it is detectable when the amplitude of the wave is nonzero, but not detectable when the amplitude is zero. This makes it appear as if the electron is teleporting from place to place around the atom. If you were somehow able to take a time-lapse picture of an electron as it moves
around the nucleus, the picture might look something like the diagram to the right.
Notice that there is a region close
to the nucleus where the electron is unlikely to be found, and a ring a little farther out where there is a high probability of finding the electron.
As you get farther and farther from the nucleus, Schrödinger’s equation predicts different shapes for these probability distributions. These regions of high probability are called “orbitals,” because of their relation to the orbits originally suggested by the planetary model.
Schrödinger was awarded the Nobel prize in physics in 1933 for this discovery.
The implications of quantum theory are vast. Among other things, the energies, shapes and numbers of orbitals in an atom is responsible for each atom’s chemical and physical properties and its location on the Periodic Table of the Elements, which means quantum mechanics is responsible for pretty much all of chemistry!
Some principles of quantum theory that are studied explicitly in chemistry include:
- atomic \& molecular orbitals
- electron configurations
- the aufbau principle
Fundamental Forces
Notes:
All forces in nature ultimately come from one of the following four forces:
strong force (or “strong nuclear force” or “strong interaction”): an attractive force between quarks. The strong force holds the nuclei of atoms together. The energy comes from converting mass to energy.
Effective range: about the size of the nucleus of an average-size atom.
weak force (or “weak nuclear force” or “weak interaction”): the force that causes protons and/or neutrons in the nucleus to become unstable and leads to beta nuclear decay. This happens because the weak force causes an up or down quark to change its flavor. (This process is described in more detail in the section on the Standard Model of Particle Physics, starting on page 589.)
Relative Strength: $10^{-6}$ to $10^{-7}$ times the strength of the strong force.
Effective range: about $1 / 3$ the diameter of an average nucleus.
electromagnetic force: the force between electrical charges. If the charges are the same (“like charges”)-both positive or both negative-the particles repel each other. If the charges are different (“opposite charges”)-one positive and one negative-the particles attract each other.
Relative Strength: about $1 / 137$ as strong as the strong force.
Effective range: $\infty$, but gets smaller as (distance) ${ }^2$.
gravitational force: the force that causes masses to attract each other. Usually only observable if one of the masses is very large (like a planet).
Relative Strength: only $10^{-39}$ times as strong as the strong force.
Effective range: $\infty$, but gets smaller as (distance) ${ }^2$.
Standard Model
Notes:
The Standard Model is a theory of particle physics that:
- identifies the particles that matter is ultimately comprised of
- describes properties of these particles, including their mass, charge, and spin
- describes interactions between these particles
The Standard Model dates to the mid-1970s, when the existence of quarks was first experimentally confirmed. Physicists are still discovering new particles and relationships between particles, so the model and the ways it is represented are evolving, much like atomic theory and the Periodic Table of the Elements was evolving at the turn of the twentieth century. The table and the model described in these notes represent our understanding, as of 2023. By the middle of this century, the Standard Model may evolve to a form that is substantially different from the way we represent it today.
The Standard Model in its present form does not incorporate dark matter, dark energy, or gravitational attraction.
The Standard Model is often presented in a table, with rows, columns, and colorcoded sections used to group subsets of particles according to their properties.
As of 2021, the Standard Model is represented by a table similar to this one:
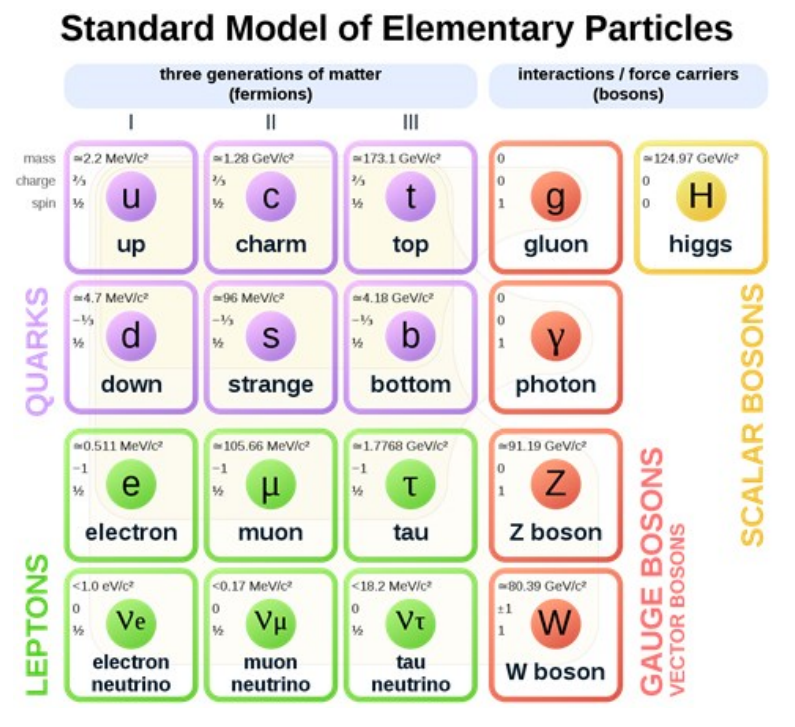
Properties shown in the table include mass, charge, and spin.
- Mass is shown in units of electron volts divided by the speed of light squared $\left(\frac{e v}{c^2}\right)$. An electron volt $(\mathrm{eV})$ is the energy acquired by an electric potential difference of one volt applied to one electron. (Recall that the metric prefix ” $\mathrm{M}^{\text {” }}$ stands for mega $\left(10^6\right)$ and the metric prefix ” $\mathrm{G}^{\prime \prime}$ stands for giga $\left(10^9\right)$.) The $c^2$ in the denominator comes from Einstein’s equation, $E=m c^2$, solved for $m$.
- Charge is the same property that we studied in the electricity unit. The magnitude and sign of charge is relative to the charge of an electron, which is defined to be -1 .
- Spin is the property that is believed to be responsible for magnetism. (The name is because magnetism was previously thought to come from a magnetic field produced by electrons spinning within their orbitals.)
Fundamental Particles
Quarks
Quarks are particles that participate in strong interactions (sometimes called the “strong force”) through the action of “color charge” (which will be described later). Because protons and neutrons (which make up most of the mass of an atom) are made of three quarks each, quarks are the subatomic particles that make up most of the ordinary matter $^*$ in the universe.
- quarks have color charge (i.e., they interact via the strong force)
- quarks have spin of $\pm 1 / 2$
- “up-type” quarks carry a charge of $+2 / 3 ;$;down-type” quarks carry a charge of $-1 / 3$.
There are six flavors ${ }^{\dagger}$ of quarks: up and down, charm and strange, and top and bottom. (Originally, top and bottom quarks were called truth and beauty.)
Leptons
Leptons are the smaller particles that make up most matter. The most familiar lepton is the electron. Leptons participate in “electroweak” interactions, meaning combinations of the electromagnetic and weak forces.
- leptons do not have color charge (i.e., they do not interact via the strong force)
- leptons have spins of $+1 / 2$
- electron-type leptons have a charge of -1 ; neutrinos do not have a charge.
- neutrinos oscillate, which makes their mass indefinite.
Gauge Bosons
Gauge bosons are the particles that carry force-their interactions are responsible for the fundamental forces of nature: the strong force, the weak force, the electromagnetic force and the gravitational force. The hypothetical particle responsible for the gravitational force is the graviton, which has not yet been detected (as of 2023).
- photons are responsible for the electromagnetic force.
- gluons are responsible for the strong interaction (strong force)
- $W$ and $z$ bosons are responsible for the weak interaction (weak force)
“Matter that is not “ordinary matter” is called “dark matter”, whose existence is theorized but not yet proven.
${ }^{+}$Yes, “flavors” really is the correct term.
Scalar Bosons
At present, the only scalar boson we know of is the Higgs boson, discovered in 2012, which is responsible for mass.

Fermions
Quarks and leptons (the left columns in the table of the Standard Model) are fermions. Fermions are described by Fermi-Dirac statistics and obey the Pauli exclusion principle (which states that no two particles in an atom may have the same exact set of quantum numbers-numbers that describe the energy states of the particle).
Fermions are the building blocks of matter. They have a spin of $1 / 2$, and each fermion has its own antiparticle (see below).
Bosons
Bosons (the right columns in the table of the Standard Model) are described by Bose-Einstein statistics, have integer spins and do not obey the Pauli Exclusion Principle. Interactions between boson are responsible for forces and mass.
Antiparticles
Each particle in the Standard Model has a corresponding antiparticle. Like chemical elements in the Periodic Table of the Elements, fundamental particles are designated by their symbols in the table of the Standard Model. Antiparticles are designated by the same letter, but with a line over it. For example, an up quark would be designated ” $u$ “, and an antiup quark would be designated ” $\bar{u}$ “.
The antiparticle of a fermion has the same name as the corresponding particle, with the prefix “anti-“, and has the opposite charge. E.g., the antiparticle of a tau neutrino is a tau antineutrino. (However, for historical reasons an antielectron is usually called a positron.) E.g., up quark carries a charge of $+2 / 3$, which means an antiup quark carries a charge of $-2 / 3$.
Each of the fundamental bosons is its own antiparticle, except for the $\mathrm{W}^{-}$boson, whose antiparticle is the $\mathrm{W}^{+}$boson.
When a particle collides with its antiparticle, the particles annihilate each other, and their mass is converted to energy $\left(E=m c^2\right)$ and released.
Composite Particles
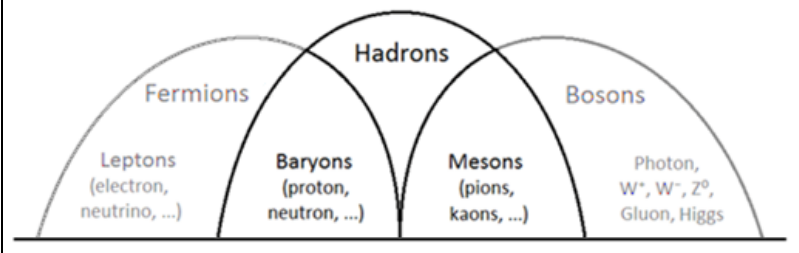
Hadrons
Hadrons are a special class of strongly-interacting composite particles (meaning that they are comprised of multiple individual particles). Hadrons can be bosons or fermions. Hadrons composed of strongly-interacting fermions are called baryons; hadrons composed of strongly-interacting bosons are called mesons.
Baryons
The most well-known baryons are protons and neutrons, which each comprised of three quarks. Protons are made of two up quarks and one down quark (“uud”), and carry a charge of +1 . Neutrons are made of one up quark and two down quarks (“udd”), and carry a charge of zero.
Some of the better-known baryons include:
- nucleons (protons \& neutrons).
- hyperons, e.g., the $\Lambda, \Sigma, \equiv$, and $\Omega$ particles. These contain one or more strange quarks, and are much heavier than nucleons.
- various charmed and bottom baryons.
- pentaquarks, which contain four quarks and an antiquark.
Mesons
Ordinary mesons are comprised of a quark plus an antiquark. Examples include the pion, kaon, and the $J / \Psi$. Mesons mediate the residual strong force between nucleons.
Some of the exotic mesons include:
- tetraquarks, which contain two quarks and two antiquarks.
- glueball, a bound set of gluons with no quarks.
- hybrid mesons, which contain one or more quark/antiquark pairs and one or more gluons.
Color Charge
Color charge is the property that is responsible for the strong nuclear interaction. All electrons and fermions (particles that have half-integer spin quantum numbers) must obey the Pauli Exclusion Principle, which states that no two particles within the same larger particle (such as a hadron or atom) can have identical sets of quantum numbers.
For electrons, (as you learned in chemistry), if two electrons share the same orbital, they need to have opposite spins. In the case of quarks, all quarks have a spin of $+1 / 2$, so in order to satisfy the Pauli Exclusion Principle, if a proton or neutron contains three quarks, there has to be some other quantum property that has different values for each of those quarks. This property is called “color charge” (or sometimes just ” color $^{* \prime \prime}$ ).
The “color” property has three values, which are called “red,” “green,” and “blue” (named after the primary colors of light). When there are three quarks in a subatomic particle, the colors have to be different, and have to add up to “colorless”. (Recall that combining each of the primary colors of light produces white light, which is colorless.)
Quarks can exchange color charge by emitting a gluon that contains one color and one anticolor. Another quark absorbs the gluon, and both quarks undergo color change. For example, suppose a blue quark emits a blue antigreen gluon:
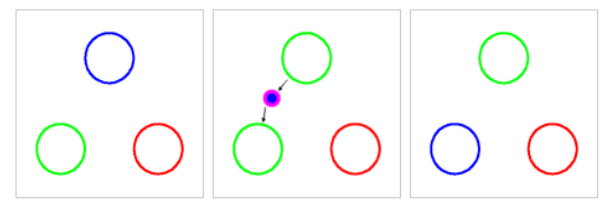
You can imagine that the quark sent away its own blue color (the “blue” in the “blue antigreen” gluon). Because it also sent out antigreen, it was left with green so it became a green quark. Meanwhile, the antigreen part of the gluon finds the green quark and cancels its color. The blue from the blue antigreen gluon causes the receiving quark to become blue. After the interaction, the particle once again has one red, one green, and one blue quark, which means color charge is conserved.
” Just like “spin” is the name of a property of energy that has nothing to do with actual spinning, “color” is a property that has nothing to do with actual color. In fact, quarks couldn’t possibly have actual color-the wavelengths of visible light are thousands of times larger than quarks!
Particle Interactions
Notes:
In particle physics, the Standard Model describes the types of particles found in nature, their properties, and how they interact. The following diagram shows which types of particles can interact with which other types.
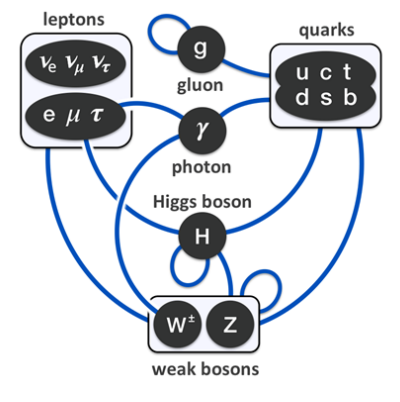
The interactions between particles can be shown pictorially in diagram called a Feynman diagram, named for American physicist Richard Feynman. The Feynman diagram tells the “story” of the interaction.
The characteristics of a Feynman diagram are:
1. Straight lines represent the motion of a particle. The arrow points to the right for a negatively-charged particle, and to the left for a positivelycharged particle
4. The x-axis is time. The interaction starts (in terms of time) on the left and proceeds from left to right.
5. The y-axis represents space. Lines coming together represent particles coming together. Lines moving apart represent particles moving away from each other. (Note that the diagram is not a map; particles can move together or apart in any direction.)
6. Each vertex, where two or more lines come together, represents an interaction.
Probably the best way to explain the diagrams is with examples.
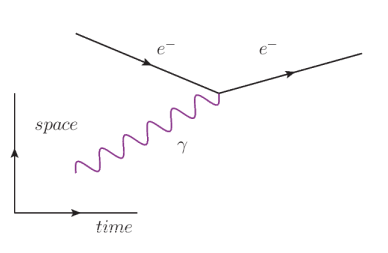
In this diagram, we start (at the left) with an electron $\left(e^{-}\right)$and photon $(\gamma)$. The two come together, and the electron absorbs the photon.
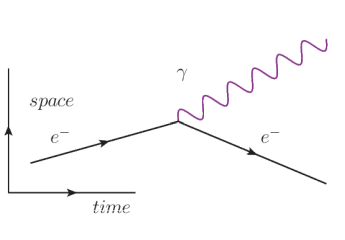
In this diagram, we start (at the left) with an electron $\left(e^{-}\right)$by itself. The electron emits a photon $(\gamma)$, but is otherwise unchanged.
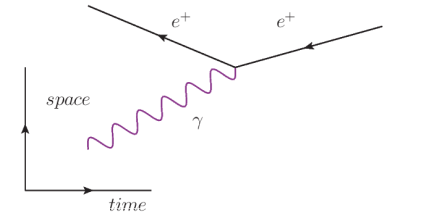
In this diagram, we start (at the left) with a positron $\left(e^{+}\right)$and photon $(\gamma)$. (Note that the arrow pointing to the left indicates a positively-charged particle.) The two come together, and the positron absorbs the photon.
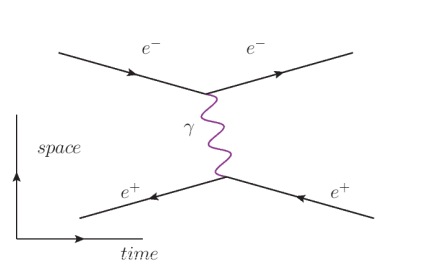
In this diagram, we start with an electron $\left(e^{-}\right)$and positron $\left(e^{+}\right)$(coming in from the left). They exchange a photon ( $(\gamma)$ between them. (Note that the diagram does not make it clear which particle emits the photon and which one absorbs it.) Then the two particles exit.
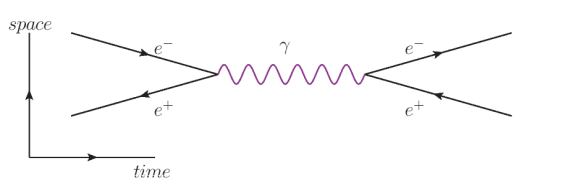
In the following diagram, we start with an electron $\left(e^{-}\right)$and positron $\left(e^{+}\right)$. They come together and annihilate each other, producing a photon $(\gamma)$. (You can tell this because for a length of time, nothing else exists except for the photon.) Then the photon pair-produces a new electron/positron pair.
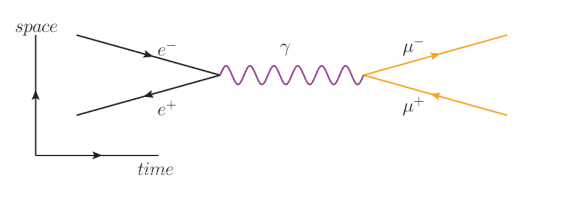
In the following diagram, an electron $\left(e^{-}\right)$and positron $\left(e^{+}\right)$annihilate each other as above, but this time the photon produces a muon $\left(\mu^{-}\right)$/antimuon $\left(\mu^{+}\right)$pair. (Again, note that the muon, which has a negative charge, has the arrow pointing to the right. The antimuon, which has a positive charge, has the arrow pointing to the left.)
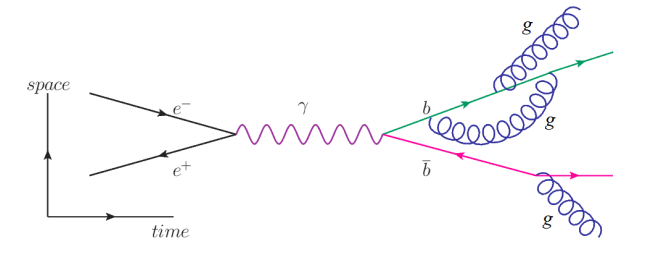
Finally, in the following diagram, an electron $\left(e^{-}\right)$and positron $\left(e^{+}\right)$annihilate each other, producing a photon $(\psi)$. The photon pair-produces a bottom quark $(b)$ and an antibottom quark $(\bar{b})$, which radiate gluons $(g)$.