Topics covered in this chapter:
Relative Motion
Notes:
Consider the following picture, taken from a moving streetcar in New Orleans:

If the streetcar is moving at a constant velocity and the track is smooth, the passengers may not notice that they are moving until they look out of the window.
In the reference frame of a person standing on the ground, the trolley and the passengers on it are moving at approximately 30 miles per hour.
In the reference frame of the trolley, the passengers sitting in the seats are stationary (not moving), and the ground is moving past the trolley at approximately 30 miles per hour.
Of course, you might want to say that the person on the ground has the “correct” reference frame. However, despite what you might prefer, neither answer is more correct than the other. Either reference frame is valid, which means either description of what is moving and what is stationary is equally valid.
Principle of Relativity
There is no experiment you can do that would allow you to determine conclusively whether or not you are moving uniformly.
Recall that “uniform motion” means moving with constant velocity, which means with a constant speed and direction. If velocity is constant, there is no acceleration, which means there is no net force.
Consider a fast airplane (such as a supersonic jet) flying from Boston to San Francisco. Imagine that the plane takes exactly three hours to fly to San Francisco, which is the same as the time difference between the two locations. Seen from outside the Earth, the situation might look like this:
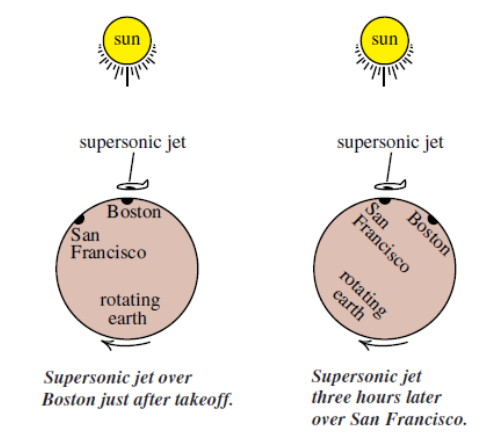
You could argue that either:
1. The jet was moving from the airspace over Boston to the airspace over San Francisco.
2. The jet was stationary and the Earth rotated underneath it. (The jet needed to burn fuel to overcome the drag from the Earth’s atmosphere as the Earth rotated, pulling its atmosphere and the jet with it.)
Of course, there are other reference frames you might consider as well.
3. Both the supersonic jet and the Earth are moving, because the Earth is revolving around the Sun with a speed of about $30000 \frac{\mathrm{m}}{\mathrm{s}}$.
4. The jet, the Earth and the Sun are all moving, because the sun is revolving around the Milky Way galaxy with a speed of about $220000 \frac{\mathrm{m}}{\mathrm{s}}$.
5. The jet, the Earth, the Sun, and the entire Milky Way galaxy are all moving through space toward the Great Attractor (a massive region of visible and dark matter about 150 million light-years away from us) with a speed of approximately $1000000 \frac{\mathrm{m}}{\mathrm{s}}$.
6. It is not clear whether there might be multiple Great Attractors, and what their motion might be relative to each other, or relative to some yet-to-bediscovered entity.
Regardless of which objects are moving with which velocities, if you are on the airplane and you drop a ball, you would observe that it falls straight down. In relativistic terms, we would say “In the reference frame of the moving airplane, the ball has no initial velocity, so it falls straight down.”
Relative Velocities
Notes:
Because the observation of motion depends on the reference frames of the observer and the object, calculations of velocity need to take these into account.
Suppose we set up a Slinky and a student sends a compression wave that moves with a velocity of $2 \frac{\mathrm{m}}{\mathrm{s}}$ along its length:
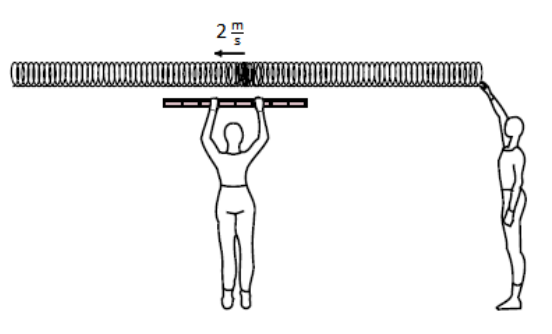
A second student holds a meter stick and times how long it takes the wave to travel from one end of the meter stick to the other. The wave would take $0.5 \mathrm{~s}$ to travel the length of the meter stick, and the student would calculate a velocity of
$
\frac{1 \mathrm{~m}}{0.5 \mathrm{~s}}=2 \frac{\mathrm{m}}{\mathrm{s}}
$
Suppose instead that the student with the meter stick is running with a velocity of $1 \frac{\mathrm{m}}{\mathrm{s}}$ toward the point of origin of the wave:

In this situation, you could use the velocities of the moving student and the wave and solve for the amount of time it would take for the wave and the end of the ruler to reach the same point. The calculation for this would be complicated, and the answer works out to be $0.33 \mathrm{~s}$, which gives a velocity of $3 \frac{\mathrm{m}}{\mathrm{s}}$.
The easier way to calculate this number is to realize that the velocity of the wave relative to the moving student is simply the sum of the velocity vectors. The velocity of the wave relative to the moving student is therefore $2 \frac{\mathrm{m}}{\mathrm{s}}+1 \frac{\mathrm{m}}{\mathrm{s}}=3 \frac{\mathrm{m}}{\mathrm{s}}$.
This $3 \frac{\mathrm{m}}{\mathrm{s}}$ is called the relative velocity, specifically the velocity of the wave relative to the moving student.
relative velocity: the apparent velocity of an object relative to an observer, which takes into account the velocities of both the object and the observer. When the object and the observer are both moving, the relative velocity is sometimes called the approach velocity.
Suppose instead that the student is running away from the point of origin (i.e., in the same direction as the wave is traveling) with a velocity of $1 \frac{\mathrm{m}}{\mathrm{s}}$ :
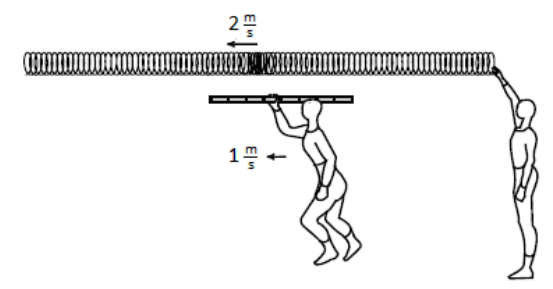
Now the relative velocity of the wave is $2 \frac{\mathrm{m}}{\mathrm{s}}-1 \frac{\mathrm{m}}{\mathrm{s}}=1 \frac{\mathrm{m}}{\mathrm{s}}$ relative to the moving student.
If the student and the wave were moving with the same velocity (magnitude and direction), the relative velocity would be zero and the wave would appear stationary to the moving student.
Speed of Light
Notes:
If the principle of relativity is true, it must be true for all measurements and all reference frames, including those involving light.
In 1864, physicist James Clerk Maxwell united four calculus equations involving magnetic and electric fields into one unified theory of light. The four equations were:
1. Gauss’s Law (which describes the relationship between an electric field and the electric charges that cause it).
2. Gauss’s Law for Magnetism (which states that there are no discrete North and South magnetic charges).
3. Faraday’s Law (which describes how a changing magnetic field creates an electric field).
4. Ampère’s Law (which describes how an electric current can create a magnetic field), including Maxwell’s own correction (which describes how a changing electric field can also create a magnetic field).
According to Maxwell’s theory, light travels as an electromagnetic wave, i.e., a wave of both electrical and magnetic energy. The moving electric field produces a magnetic field, and the moving magnetic field produces an electric field. Thus the electric and magnetic fields of the electromagnetic wave reinforce each other as they travel through space.
From Maxwell’s equations, starting from the measured values for two physical constants: the electric permittivity of free space $\left(\varepsilon_0\right)$ and the magnetic permeability of a vacuum $\left(\mu_o\right)$, Maxwell determined that the speed of light in a vacuum must be:
$
c=\frac{1}{\sqrt{\mu_o \varepsilon_o}}=2.99792458 \times 10^8 \frac{\mathrm{m}}{\mathrm{s}}^*
$
Both $\mu_0$ and $\varepsilon_0$ are physical constants, which do not depend on the reference frame. Maxwell theorized that the speed of light in a vacuum must therefore also be a physical constant, and it therefore cannot depend on the reference frame that is used to measure it.
This means:
1. Light travels at a constant velocity, regardless of whether the light is produced by something that is moving or stationary.
2. The velocity of light is the same in all reference frames. This means a photon of light moves at the same velocity, regardless of whether that velocity is measured by an observer who is stationary or by an observer who is moving.
If the wave in the above relative velocity examples was a beam of laser light instead of a Slinky, and the observer was running at a relativistic speed (meaning a speed close to the speed of light), the velocity of the light, both students would measure exactly the same velocity for the light!
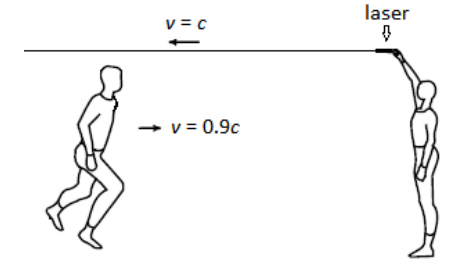
Because the speed of light (in a vacuum) is a constant, we use the variable $c$ (which stands for “constant”) to represent it in equations.
* This is an exact value as defined by the International Committee for Weights and Measures in 2019 and is one of the seven Defining Constants used to determine exact values of other constants in the International System of Units (SI).
This idea seemed just as strange to $19^{\text {th }}$ century physicists as it does today, and most physicists did not believe Maxwell for more than 45 years, when Albert Einstein published his theory of special relativity in 1905. However, several experiments have confirmed Maxwell’s conclusion, and no experiment has ever successfully refuted it.
Light travels through a vacuum (empty space) with a velocity of exactly $2.99792458 \times 10^8 \frac{\mathrm{m}}{\mathrm{s}}$. However while the speed of light does not depend on the reference frame, it does depend on the medium it is traveling through. (For more information, see the Refraction section on page 512.) When light travels through matter, (e.g., air, glass, plastic, etc.), the velocity can be substantially slower.
Length Contraction & Time Dilation
Notes:
Based on Maxwell’s conclusions, if an observer were somehow running with a relativistic speed of light toward an oncoming beam of light, the student should measure the same velocity of light as a stationary observer:
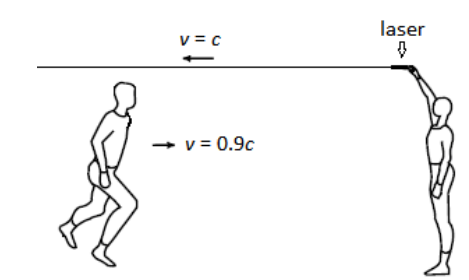
However, the amount of time it takes for a photon of light to pass the moving observer must be significantly less than the amount of time it would take a photon to pass a stationary observer.
Because velocity depends on distance and time, if the velocity of light cannot change, then as the observer approaches the speed of light, this means the distance and/or time must change!
For most people, the idea that distance and time depend on the reference frame is just as strange and uncomfortable as the idea that the speed of light cannot depend on the reference frame.
Length Contraction
If an object is moving at relativistic speeds and the velocity of light must be constant, then distances must become shorter as velocity increases. This means that as the velocity of an object approaches the speed of light, distances in its reference frame approach zero.
The Dutch physicist Hendrick Lorentz determined that the apparent change in length should vary according to the formula:
$
L=L_o \sqrt{1-v^2 / c^2}
$
where:
$L=$ length of moving object
$L_0=$ “proper length” of object (length of object at rest)
$V=$ velocity of object
$c=$ velocity of light
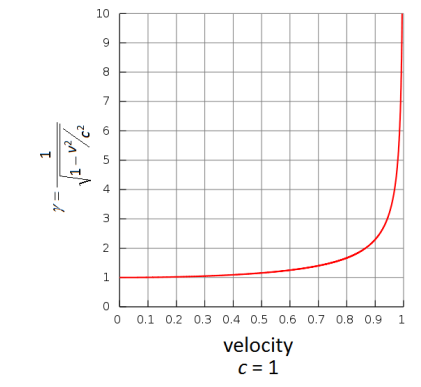
The ratio of $L_0$ to $L$ is named after Lorentz and is called the Lorentz factor $(\gamma)$ :
$
\gamma=\frac{1}{\sqrt{1-v^2 / c^2}}
$
The contracted length is therefore given by the equations:
$
L=\frac{L_0}{\gamma} \quad \text { or } \quad \frac{L_o}{L}=\gamma=\frac{1}{\sqrt{1-v^2 / c^2}}
$
The Lorentz factor,$ γ$ , is 1 at rest and approaches infinity as the velocity approaches the speed of light:
Time Dilation
In order to imagine how time is affected at relativistic speeds, imagine a clock that keeps time by sending a pulse of light from point (A), bouncing it off a mirror at point (B) and then measuring the time it takes to reach a detector back at point (A). The distance between the two surfaces is $L$, and the time for a pulse of light to travel to the mirror and back is therefore $\Delta t=\frac{2 L}{c}$.
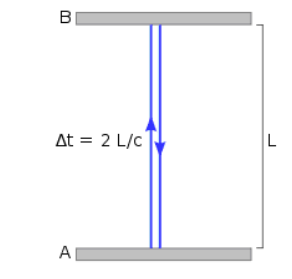
However, suppose the clock is moving at a relativistic speed. In the moving reference frame the situation looks exactly like the situation above. However, from an inertial (stationary) reference frame, the situation would look like the following:
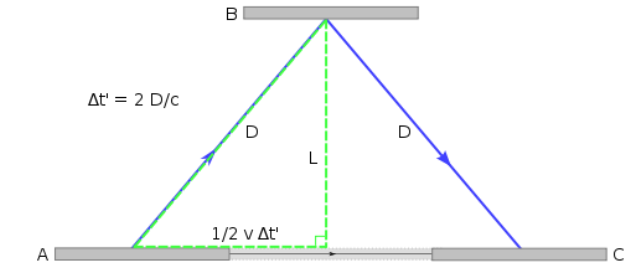
Notice that in the stationary reference frame, the pulses of light must travel farther because of the motion of the mirror and detector. Because the speed of light is constant, the longer distance takes a longer time.
In other words, time is longer in the inertial (stationary) reference frame than it is in the moving reference frame!
This conclusion has significant consequences. For example, events that happen in two different locations could be simultaneous in one reference frame, but occur at different times in another reference frame!
Using arguments similar to those for length contraction, the equation for time dilation turns out to be:
$
\Delta t^{\prime}=\gamma \Delta t \quad \text { or } \quad \frac{\Delta t^{\prime}}{\Delta t}=\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}
$
where:
$\Delta t^{\prime}=$ time difference between two events in stationary reference frame
$\Delta t=$ time difference between two events in moving reference frame
$v=$ velocity of moving reference frame
$c=$ velocity of light
Effect of Gravity on Time
Albert Einstein first postulated the idea that gravity slows down time in his paper on special relativity. This was confirmed experimentally in 1959.
As with relativistic time dilation, gravitational time dilation relates a duration of time in the absence of gravity ( “proper time”) to a duration in a gravitational field. The equation for gravitational time dilation is:
$
\Delta t^{\prime}=\Delta t \sqrt{1-\frac{2 G M}{r c^2}}
$
where:
$\Delta t^{\prime}=$ time difference between two events in stationary reference frame
$\Delta t=$ time difference between two events in moving reference frame
$G=$ universal gravitational constant $\left(6.67 \times 10^{-11} \frac{\mathrm{N} \cdot \mathrm{m}^2}{\mathrm{~kg}^2}\right)$
$M=$ mass of the object creating the gravitational field
$r=$ observer’s distance (radius) from the center of the massive object
$c=$ velocity of light
In 2014, a new atomic clock was built at the University of Colorado at Boulder, based on the vibration of a lattice of strontium atoms in a network of crisscrossing laser beams. The clock has been improved even since its invention, and is now accurate to better than one second per fifteen billion years (the approximate age of the universe). This clock is precise enough to measure differences in time caused by differences in the gravitational pull of the Earth near Earth surface. This clock would run measurably faster on a shelf than on the floor, because of the differences in time itself due to the Earth’s gravitational field.
Black Holes
A black hole is an object that is so dense that its escape velocity (from physics 1 ) is faster than the speed of light, which means even light cannot escape.
For this to happen, the radius of the black hole needs to be smaller than $\frac{2 G M}{c^2}$.
This results in a negative value for $\sqrt{1-\frac{2 G M}{r c^2}}$, which makes $\Delta t^{\prime}$ imaginary.
The consequence of this is that time is imaginary (does not pass) on a black hole, and therefore light cannot escape. This critical value for the radius is called the Schwarzschild radius, named for the German astronomer Karl Schwarzschild who first solved Einstein’s field equations exactly in 1916 and postulated the existence of black holes.
The sun is too small to be able to form a black hole, but if it could, the Schwarzschild radius would be approximately $3.0 \mathrm{~km}$ for the Sun, and approximately $9.0 \mathrm{~mm}$ for the Earth.
Sample problem:
Q: In order to avoid detection by the Borg, the starship Enterprise must make itself appear to be less than $25 \mathrm{~m}$ long. If the rest length of the Enterprise is $420 \mathrm{~m}$, how fast must it be traveling? What fraction of the speed of light is this?
Answer/Explanation
A: $L=25 \mathrm{~m}$
$
\begin{aligned}
L_0 & =420 \mathrm{~m} \\
c & =2.998 \times 10^8 \frac{\mathrm{m}}{\mathrm{s}}
\end{aligned}
$
$\gamma=\frac{L_0}{L}=\frac{1}{\sqrt{1-V^2 / C^2}}$ $\frac{v^2}{8.988 \times 10^{16}}=1-0.00354=0.99646$
$\frac{420}{25}=\frac{1}{\sqrt{1-v^2 /\left(2.998 \times 10^8\right)^2}}$ $v^2=(0.99646)\left(8.988 \times 10^{16}\right)$ $v^2=8.956 \times 10^{16}$
$\frac{25}{420}=0.0595=\sqrt{1-v^2 /\left(2.998 \times 10^8\right)^2}$
$
\begin{aligned}
& v=\sqrt{8.956 \times 10^{16}}=2.993 \times 10^8 \frac{\mathrm{m}}{\mathrm{s}} \\
& \frac{2.993 \times 10^8}{2.998 \times 10^8}=0.998 \mathrm{C}
\end{aligned}
$
$
(0.0595)^2=0.00354=1-\frac{v^2}{8.988 \times 10^{16}}
$
Energy-Momentum Relation
Notes:
The momentum of an object also changes according to the Lorentz factor as it approaches the speed of light:
$
p=\gamma p_o \quad \text { or } \quad \frac{p}{p_o}=\gamma=\frac{1}{\sqrt{1-v^2 / c^2}}
$
where:
$p=$ momentum of object in moving reference frame
$p_0=$ momentum of object in stationary reference frame
$v=$ velocity of moving reference frame
$c=$ velocity of light
Because momentum is conserved, an object’s momentum in its own reference frame must remain constant. Therefore, at relativistic speeds the object’s mass must change!
The equation for relativistic mass is:
$
m=\gamma m_o \quad \text { or } \quad \frac{m}{m_o}=\gamma=\frac{1}{\sqrt{1-v^2 / c^2}}
$
where:
$
\begin{aligned}
m & =\text { mass of object in moving reference frame } \\
m_0 & =\text { mass of object at rest }
\end{aligned}
$
Therefore we can write the momentum equation as:
$p=\gamma m_o v$
Note that as the velocity of the object approaches the speed of light, the
denominator of the Lorentz factor, $\sqrt{1-v^2 / c^2}$ approaches zero, which means that the Lorentz factor approaches infinity.
Therefore the momentum of an object must also approach infinity as the velocity of the object approaches the speed of light.
This relationship creates a potential problem. An object with infinite momentum must have infinite kinetic energy, but Einstein’s equation $E=m c^2$ is finite. While it is true that the relativistic mass becomes infinite as velocity approaches the speed of light, there is still a discrepancy. Recall from mechanics that:
$
E_k=\frac{p^2}{2 m}
$
According to this formula, the energy predicted using relativistic momentum should increase faster than the energy predicted by using $E=m c^2$ with relativistic mass. Obviously the amount of energy cannot depend on how the calculation is performed; the problem must therefore be that Einstein’s equation needs a correction for relativistic speeds.
The solution is to modify Einstein’s equation by adding a momentum term. The resulting energy-momentum relation is:
$
E^2=(p c)^2+\left(m c^2\right)^2
$
This equation gives results that are consistent with length contraction, time dilation and relativistic mass.
For an object at rest, its momentum is zero, and the equation reduces to the familiar form:
$
\begin{gathered}
E^2=0+\left(m c^2\right)^2 \\
E=m c^2
\end{gathered}
$