Topics covered in this chapter:
Heat & Temperature
Notes:
Heat is energy that is stored as the translational kinetic energy of the particles that make up an object or substance.
You may remember from chemistry that particles (atoms or molecules) are always moving (even at absolute zero), and that energy can transfer via elastic collisions between the particles of one object or substance and the particles of another.
Note that heat is the energy itself, whereas temperature is a measure of the quality of the heat-the average of the kinetic energies of the individual molecules:
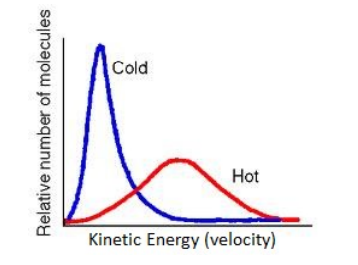
Note that the particles of a substance have a range of kinetic energies, and the temperature is the average. Notice that when a substance is heated, the particles acquire a wider range of kinetic energies, with a higher average.
When objects are placed in contact, heat is transferred from each object to the other via the transfer of momentum that occurs when the individual molecules collide. Molecules that have more energy transfer more energy than they receive. Molecules that have less energy receive more energy than they transfer. This means three things:
1. Individual collisions transfer energy in both directions. The particles of a hot substance transfer energy to the cold substance, but the particles of the cold substance also transfer energy to the hot substance.
2. The net (overall) flow of energy is from objects with a higher temperature (more kinetic energy) to objects with a lower temperature (less kinetic energy). I.e., more energy is transferred from the hot substance to the cold substance than vice versa.
3. If you wait long enough, all of the molecules will have the same temperature (i.e., the same average kinetic energy).
This means that the temperature of one object relative to another determines which direction the heat will flow, much like the way the elevation (vertical position) of one location relative to another determines which direction water will flow.
However, the total heat (energy) contained in an object depends on the mass as well as the temperature, in the same way that the total change in energy of the water going over a waterfall depends on the mass of the water as well as the height.
Consider two waterfalls, one of which is twice the height of the second, but the second of which has ten times as much water going over it as the first:
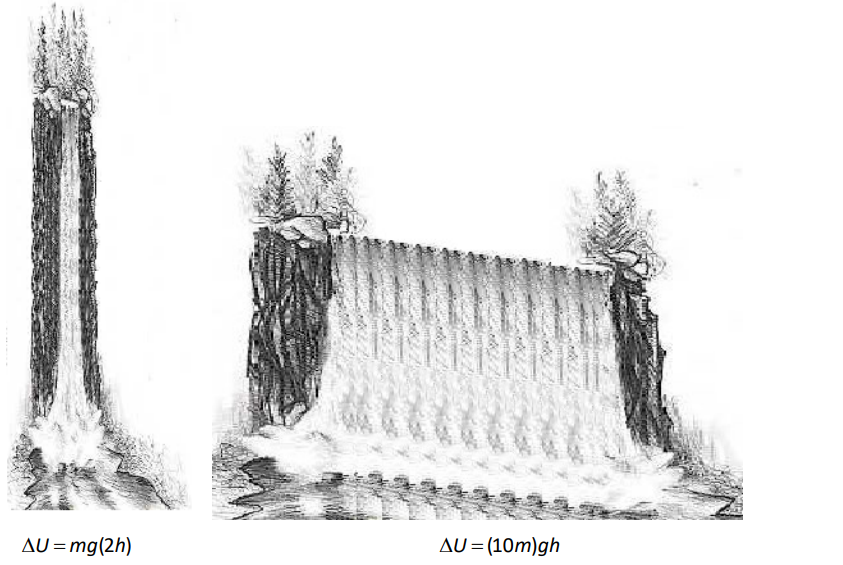
In the above pictures, each drop of water falling from the waterfall on the left has more gravitational potential energy, but more total energy goes over the waterfall on the right.
Similarly, each particle in an object at a higher temperature has more thermal energy than each particle in another object at a lower temperature.
If we built a waterway between the two falls, water could flow from the top of the first waterfall to the top of the second, but not vice versa.
Similarly, the net flow of heat is from a smaller object with higher temperature to a larger object with a lower temperature, but not vice versa.
Heat Flow
system: the region or collection of objects under being considered in a problem.
surroundings: everything that is outside of the system.
E.g., if a metal block is heated, we would most likely define the system to be the block, and the surroundings to be everything else.
We generally use the variable $Q$ to represent heat in physics equations.
Heat flow is always represented in relation to the system.
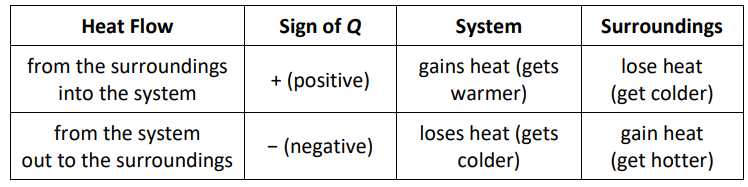
A positive value of $Q$ means heat is flowing into the system. Because the heat is transferred from the molecules outside the system to the molecules in the system, the energy of the system increases, and the energy of the surroundings decreases.
A negative value of $Q$ means heat is flowing out of the system. Because the heat is transferred from the molecules in the system to the molecules outside the system, the energy of the system decreases, and the energy of the surroundings increases.
This can be confusing. Suppose you set a glass of ice water on a table. When you pick up the glass, your hand gets colder because heat is flowing from your hand (which is part of the surroundings) into the system (the glass of ice water). This means the system (the glass of ice water) is gaining heat, and the surroundings (your hand, the table, etc.) are losing heat. The value of $Q$ would be positive in this example.
In simple terms, you need to remember that your hand is part of the surroundings, not part of the system.
thermal equilibrium: when all of the particles in a system have the same average kinetic energy (temperature). When a system is at thermal equilibrium, no net heat is transferred. (I.e., collisions between particles may still transfer energy, but the average temperature of the particles in the system-what we measure with a thermometer-is not changing.)
Heat Transfer
Notes:
Heat transfer is the flow of heat energy from one object to another. Heat transfer usually occurs through three distinct mechanisms: conduction, radiation, and convection.
conduction: transfer of heat through collisions of particles by objects that are in direct contact with each other. Conduction occurs when there is a net transfer of momentum from the molecules of an object with a higher temperature transfer to the molecules of an object with a lower temperature.
thermal conductivity $(k)$ : a measure of the amount of heat that a given length of a substance can conduct in a specific amount of time. Thermal conductivity is measured in units of $\frac{\mathrm{J}}{\mathrm{m} \cdot \mathrm{s}^{\circ} \mathrm{C}}$ or $\frac{\mathrm{w}}{\mathrm{m}^{\circ} \mathrm{C}}$.
conductor: an object that allows heat to pass through itself easily; an object with high thermal conductivity.
insulator: an object that does not allow heat to pass through itself easily; a poor conductor of heat; an object with low thermal conductivity.
radiation: transfer of heat through space via electromagnetic waves (light, microwaves, etc.)
convection: transfer of heat by motion of particles that have a higher temperature exchanging places with particles that have a lower temperature. Convection usually occurs when air moves around a room.
Natural convection occurs when particles move because of differences in density. In a heated room, because cool air is more dense than warm air, the force of gravity is stronger on the cool air, and it is pulled harder toward the ground than the warm air. The cool air displaces the warm air, pushing it upwards out of the way.
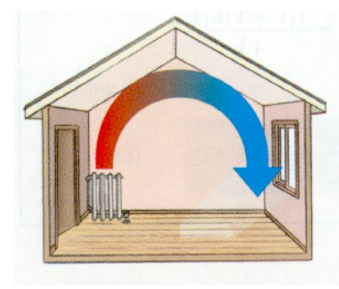
In a room with a radiator, the radiator heats the air, which causes it to expand and be displaced upward by the cool air nearby. When the (less dense) warm air reaches the ceiling, it spreads out, and it continues to cool as it spreads. When the air reaches the opposite wall, it is forced downward toward the floor, across the floor, and back to the radiator.
Forced convection can be achieved by moving heated or cooled air using a fan. Examples of this include ceiling fans and convection ovens. If your radiator does not warm your room enough in winter, you can use a fan to speed up the process of convection. (Make sure the fan is moving the air in the same direction that would happen from natural convection. Otherwise, the fan will be fighting against physics!)
Calculating Heat Transfer by Conduction
Heat transfer by conduction can be calculated using Fourier’s Law of Heat
Conduction:
$
P=\frac{Q}{t}= \pm k A \frac{\Delta T}{L}
$
where:
$
\begin{aligned}
& P=\text { power }(\mathrm{W}) \\
& Q=\text { heat transferred }(\mathrm{J}) \\
& t=\text { time }(\mathrm{s}) \\
& k=\text { coëfficient of thermal conductivity }\left(\frac{\mathrm{W}}{\mathrm{m}^{\circ} \cdot \mathrm{C}}\right) \\
& A=\text { cross-sectional area }\left(\mathrm{m}^2\right) \\
& \Delta T=\text { temperature difference }\left(\mathrm{K} \text { or }{ }^{\circ} \mathrm{C}\right) \\
& L=\text { length }(\mathrm{m})
\end{aligned}
$
The \pm sign means that the value can be positive or negative, because the sign for $Q$ is chosen based on whether the heat transfers into $(+)$ or out of $(-)$ the system.
Note that for insulation (the kind you have in the walls and attic of your home), you want the lowest possible thermal conductivity-you don’t want the insulation to conduct the heat from the inside of your house to the outside! Because most people think that bigger numbers are better, the industry has created a measure of the effectiveness of insulation called the “R value”. It is essentially the reciprocal of $\frac{k}{L}$, which means lower conductivity and more thickness gives better insulation.
Sample Problem:
Q: A piece of brass is $5.0 \mathrm{~mm}(0.0050 \mathrm{~m})$ thick and has a cross-sectional area of $0.010 \mathrm{~m}^2$. If the temperature on one side of the metal is $65^{\circ} \mathrm{C}$ and the temperature on the other side is $25^{\circ} \mathrm{C}$, how much heat will be conducted through the metal in 30 . s? The coefficient of thermal conductivity for brass is $120 \frac{\mathrm{w}}{\mathrm{m} \cdot{ }^{\circ} \mathrm{C}}$.
Answer/Explanation
$
\begin{aligned}
A: \frac{Q}{t} & =k A \frac{\Delta T}{L} \\
\frac{Q}{30} & =(120)(0.010)\left(\frac{65-25}{0.0050}\right)=9600 \\
Q & =288000 \mathrm{~J}=288 \mathrm{~kJ}
\end{aligned}
$
Calculating Heat Transfer by Radiation
Heat transfer by radiation is based on the temperature of a substance and its ability emit heat (emissivity). The equation is:
$
P=\frac{Q}{t}=\varepsilon \sigma A T^4
$
where:
$
\begin{aligned}
P & =\text { power }(\mathrm{W}) \\
Q & =\text { heat }(\mathrm{J}) \\
t & =\text { time }(\mathrm{s}) \\
\varepsilon & =\text { emissivity (dimensionless; “black body” } \equiv 1) \\
\sigma & =\text { Stefan-Boltzmann constant }\left(\sigma=5.67 \times 10^{-8} \frac{\mathrm{W}}{\mathrm{m}^2 \cdot \mathrm{k}^4}\right) \\
A & =\operatorname{area}\left(\mathrm{m}^2\right) \\
T & =\text { temperature }(\mathrm{K})
\end{aligned}
$
Note that because the equation contains $T$ (rather than $\Delta T$ ), the temperature needs to be in Kelvin.
emissivity $(\varepsilon)$ : a ratio of the amount of heat radiated by a substance to the amount of heat that would be radiated by a perfect “black body” of the same dimensions.
Emissivity is a dimensionless number (meaning that it has no units, because the units cancel), and is specific to the substance.
black body: an object that absorbs all of the heat energy that comes in contact with it (and reflects none of it).
Stefan-Boltzmann constant $(\sigma)$ : the constant that makes the above equation come out in watts. Note that the Stefan-Boltzmann constant is defined from other constants:
$\sigma=\frac{2 \pi^5 k_B^4}{15 h^3 c^2}$, where $k_B$ is the Boltzmann constant, $h$ is Planck’s constant, and $c$ is the speed of light in a vacuum.
Energy Conversion
Notes:
The law of conservation of energy states that total energy is always conserved, but that energy can be converted from one form to another.
We have already seen this in mechanics with the conversion between gravitational potential energy and kinetic energy.
Heat is energy. Like other forms of energy, it can do work. For example, in a steam engine, heat is used to boil water in a sealed container. As more water boils, there is more gas in the boiler, which makes the pressure increase. If the gas can only expand by pushing against something (like a piston), the force from the pressure can do work by moving the piston and whatever it’s connected to. (We will revisit the concept of pressure as a force when we study fluid mechanics. For now, it’s enough to understand that heat energy can be converted to kinetic energy.)
In mechanics, recall that collisions can be elastic or inelastic. In an elastic collision, kinetic energy is conserved; in an inelastic collision, some of the kinetic energy is converted to other forms, mostly heat.
We can use the law of conservation of energy to estimate the amount of energy converted to heat in a completely inelastic collision.
Consider a $0.150 \mathrm{~kg}$ tomato hitting the wall at a velocity of $20.0 \frac{\mathrm{m}}{\mathrm{s}}$.

After the collision, the velocity of the tomato and the wall are both zero. This means the kinetic energy of the tomato after the collision is zero. Because energy must be conserved, this means all of the kinetic energy from the tomato must have been converted to heat.
$
\begin{aligned}
& E_k=\frac{1}{2} m v^2 \\
& E_k=\left(\frac{1}{2}\right)(0.150)(20.0)^2=30.0 \mathrm{~J}
\end{aligned}
$
Now consider the same splat tomato with a mass of $0.150 \mathrm{~kg}$ and a velocity of $20.0 \frac{\mathrm{m}}{\mathrm{s}}$ hitting a $1.00 \mathrm{~kg}$ block of wood that is initially at rest. This is still an inelastic collision, but now the wood is free to move, which means it has kinetic energy after the collision.
To solve this problem, we need to use conservation of momentum to find the velocity of the splat tomato + wood after the collision, and then use the velocity before and after to calculate the change in kinetic energy.
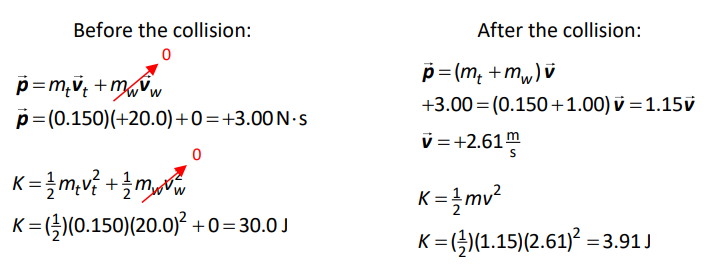
This means there is $30.0-3.91=26.1 \mathrm{~J}$ of kinetic energy that is “missing” after the collision. This “missing” energy is mostly converted to heat. If you could measure the temperature of the “splat tomato” and the wood extremely accurately before and after the collision, you would find that both would be warmer as a result of the “missing” $26.1 \mathrm{~J}$ of energy.
Specific Heat Capacity \& Calorimetry
Notes:
Different objects have different abilities to hold heat. For example, if you enjoy pizza, you may have noticed that the sauce holds much more heat (and burns your mouth much more readily) than the cheese or the crust.
The amount of heat that a given mass of a substance can hold is based on its specific heat capacity.
” Calorimetry is usually taught in chemistry classes. However, the topic was moved from chemistry to physics in the Massachusetts Curriculum Frameworks starting in 2016.
specific heat capacity $(C)$ : a measure of the amount of heat required per gram of a substance to produce a specific temperature change in the substance.
$C_p$ : specific heat capacity, measured at constant pressure. For gases, this means the measurement was taken allowing the gas to expand as it was heated.
$C_v:$ specific heat capacity, measured at constant volume. For gases, this means the measurement was made in a sealed container, allowing the pressure to rise as the gas was heated.
For solids and liquids, $C_p \approx C_v$ because the pressure and volume change very little as they are heated. For gases, $C_p>C_v$ (always). For ideal gases, $C_p-C_v=R$, where $R$ is a constant known as “the gas constant.”
When there is a choice, $C_p$ is more commonly used than $C_v$ because it is easier to measure. When dealing with solids and liquids, most physicists just use $C$ for specific heat capacity and don’t worry about the distinction.
Calculating Heat from a Temperature Change
The amount of heat gained or lost when an object changes temperature is given by the equation:
$
Q=m C \Delta T
$
Where:$
\begin{aligned}
& Q=\text { heat }(\mathrm{J} \text { or } \mathrm{kJ}) \\
& m=\text { mass }(\mathrm{g} \text { or } \mathrm{kg}) \\
& C=\text { specific heat capacity }\left(\frac{\mathrm{kJ}}{\mathrm{kg} \cdot \mathrm{K}}\right) \\
& \Delta T=\text { temperature change }\left(\mathrm{K} \text { or }{ }^{\circ} \mathrm{C}\right)
\end{aligned}
$
Because problems involving heat often involve large amounts of energy, specific heat capacity is often given in kilojoules per kilogram per degree Celsius.
Note that $1 \frac{\mathrm{kJ}}{\mathrm{kg} \cdot \mathrm{K}} \equiv 1 \frac{\mathrm{kJ}}{\mathrm{kg} \cdot \cdot{ }^{\circ} \mathrm{C}} \equiv 1 \frac{\mathrm{J}}{\mathrm{g} \cdot{ }^{\circ} \mathrm{C}} \quad$ and $\quad 1 \frac{\mathrm{cal}}{\mathrm{g} \cdot{ }^{\circ} \mathrm{C}} \equiv 1 \frac{\mathrm{kcal}}{\mathrm{kg} \cdot{ }^{\circ} \mathrm{C}}=4.18 \frac{\mathrm{J}}{\mathrm{g} \cdot{ }^{\circ} \mathrm{C}}=4.18 \frac{\mathrm{kJ}}{\mathrm{kg} \cdot \mathrm{K}}$
You need to be careful with the units. If the mass is given in kilograms (kg), your specific heat capacity will have units of $\frac{\mathrm{kJ}}{\mathrm{kg} \cdot{ }^{\circ} \mathrm{C}}$ and the heat energy will come out in kilojoules $(\mathrm{kJ})$. If mass is given in grams, you will use units of $\frac{\mathrm{J}}{\mathrm{g} \cdot{ }^{\circ} \mathrm{C}}$ and the heat energy will come out in joules (J).
“Because $1 \mathrm{~K}$ is the same size as $1^{\circ} \mathrm{C}$, the two units are equivalent for $\Delta T$ values. Note, however, that $T$ in equations must be in kelvin, because a temperature of 0 must mean absolute zero.
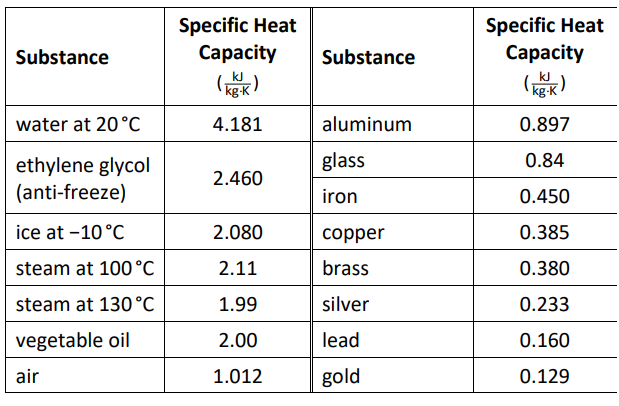
Specific Heat Capacities of Some Substances
Calorimetry
calorimetry: the measurement of heat flow
In a calorimetry experiment, heat flow is calculated by measuring the mass and temperature change of an object and applying the specific heat capacity equation.
calorimeter: an insulated container for performing calorimetry experiments.
coffee cup calorimeter: a calorimeter that is only an insulated container-it does not include a thermal mass (such as a mass of water). It is usually made of Styrofoam, and is often nothing more than a Styrofoam coffee cup.
bomb calorimeter: a calorimeter for measuring the heat produced by a chemical reaction. A bomb calorimeter is a double-wall metal container with water between the layers of metal. The heat from the chemical reaction makes the temperature of the water increase. Because the mass and specific heat of the calorimeter (water and metal) are known, the heat produced by the reaction can be calculated from the increase in temperature of the water.
It has a great name, but a bomb calorimeter doesn’t involve actually blowing anything up.
Solving Coffee Cup Calorimetry Problems
Most coffee cup calorimetry problems involve placing a hot object in contact with a colder one. Many of them involve placing a hot piece of metal into cold water.
To solve the problems, assume that both objects end up at the same temperature.
If we decide that heat gained (going into a substance) by each object that is getting hotter is positive, and heat lost (coming out of a substance) by every substance that is getting colder is negative, then the basic equation is:
Heat Lost + Heat Gained $=$ Change in Thermal Energy
$
\sum Q_{\text {lost }}+\sum Q_{\text {gained }}=\Delta Q
$
If the calorimeter is insulated, then no heat is gained or lost by the entire system (which means $\Delta Q=0$ ).
If we have two substances (\#1 and \#2), one of which is getting hotter and the other of which is getting colder, then our equation becomes:
Heat Lost + Heat Gained $=$ Change in Thermal Energy
$
\begin{aligned}
& \sum Q_{\text {lost }}+\sum Q_{\text {gained }}=\Delta Q=0 \\
& m_1 C_1 \Delta T_1+m_2 C_2 \Delta T_2=0
\end{aligned}
$
In this example, $\Delta T_1$ would be negative and $\Delta T_2$ would be positive.
To solve a calorimetry problem, there are six quantities that you need: the two masses, the two specific heat capacities, and the two temperature changes. (You might be given initial and final temperatures for either or both, in which case you’ll need to subtract. Remember that if the temperature increases, $\Delta T$ is positive, and if the temperature decreases, $\Delta T$ is negative.) The problem will usually give you all but one of these and you will need to find the missing one.
If you need to find the final temperature, use $\Delta T=T_f-T_i$ on each side. You will have both $T_i$ numbers, so the only variable left will be $T_f$. (The algebra is straightforward, but ugly.)
Sample Problems:
Q: An $0.050 \mathrm{~kg}$ block of aluminum is heated and placed in a calorimeter containing $0.100 \mathrm{~kg}$ of water at $20 .{ }^{\circ} \mathrm{C}$. If the final temperature of the water was $30 .{ }^{\circ} \mathrm{C}$, to what temperature was the aluminum heated?
Answer/Explanation
A: To solve the problem, we need to look up the specific heat capacities for aluminum and water in Table I. Thermal Properties of Selected Materials on page 634 of your Physics Reference Tables. The specific heat capacity of aluminum is $0.898 \frac{\mathrm{J}}{\mathrm{g} \cdot \mathrm{C}}$, and the specific heat capacity for water is $4.181 \frac{\mathrm{J}}{\mathrm{g} \cdot \mathrm{C}}$.
We also need to realize that we are looking for the initial temperature of the aluminum. $\Delta T$ is always final – initial, which means $\Delta T_{A 1}=30-T_{i, A 1}$. (Because the aluminum starts out at a higher temperature, this will give us a negative number, which is what we want.)
Phase Diagrams*
Notes:
The phase of a substance (solid, liquid, gas) depends on its temperature and pressure.
phase diagram: a graph showing the phase(s) present at different temperatures and pressures.
* Phase diagrams are usually taught in chemistry. However, they relate to the topics of phase changes and heating curves, which were moved from chemistry to physics in the Massachusetts Curriculum Frameworks starting in 2016.
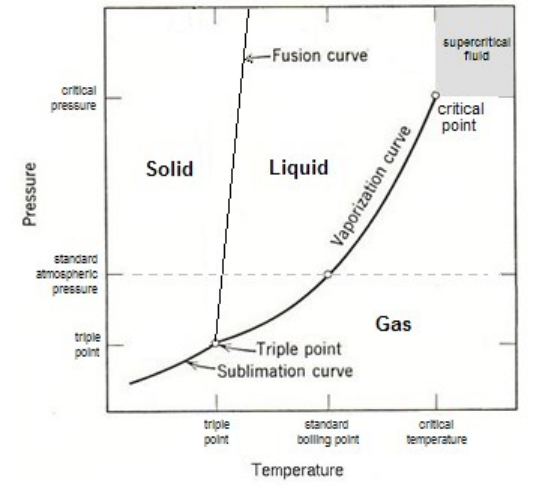
fusion curve: the set of temperatures and pressures at which a substance melts/freezes.
vaporization curve: the set of temperatures \& pressures at which a substance vaporizes/condenses.
sublimation curve: the set of temperatures \& pressures at which a substance sublimes/deposits.
triple point: the temperature and pressure at which a substance can exist simultaneously as a solid, liquid, and gas.
critical point: the highest temperature at which the substance can exist as a liquid. The critical point is the endpoint of the vaporization curve.
supercritical fluid: a substance whose temperature and pressure are above the critical point. The substance would be expected to be a liquid (due to the pressure), but the molecules have so much energy that the substance behaves more like a gas.
Phase Diagram for Water

Note that pressure is on a logarithmic scale, and that standard atmospheric pressure is 1 bar $\approx 1 \mathrm{~atm}$.
Note also that the temperature is in kelvin. To convert degrees Celsius to kelvin, add 273. (e.g., $25^{\circ} \mathrm{C}+273=298 \mathrm{~K}$.)
Notice that the slope of the fusion curve (melting/freezing line) is negative. This is because ice $I$ is less dense than liquid water. At temperatures near the melting point and pressures less than about 2000 bar, increasing the pressure will cause ice to melt. Water is one of the only known substances that exhibits this behavior.
Phase Diagram for Carbon Dioxide
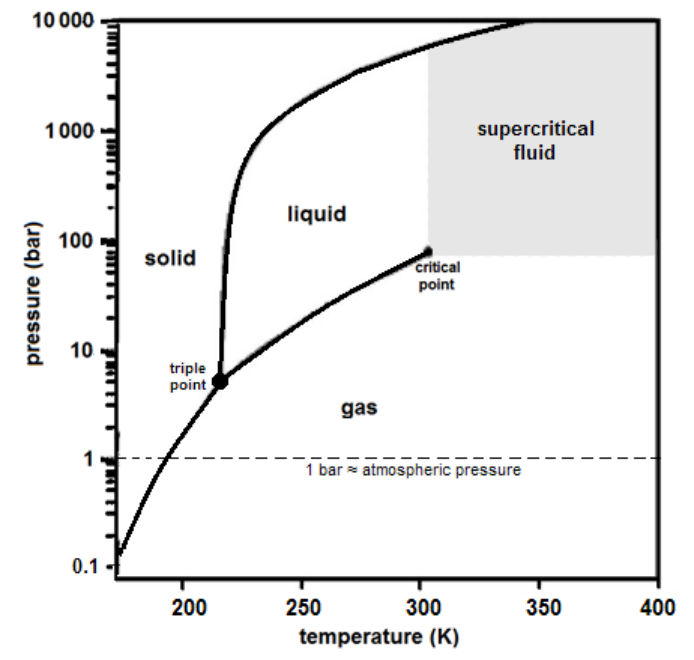
Notice that the pressure of the triple point for $\mathrm{CO}_2$ is about $5 \mathrm{bar}$, which means $\mathrm{CO}_2$ cannot be a liquid at atmospheric pressure. This is why dry ice (solid $\mathrm{CO}_2$ ) sublimes directly from a solid to a gas.
Phases & Phase Changes
Notes:
macroscopic: objects or bulk properties of matter that we can observe directly.
microscopic: objects or properties of matter that are too small to observe directly.
Note that macroscopic properties of a substance are often determined by microscopic interactions between the individual molecules. ${ }^{\dagger}$
phase: a term that relates to how rigidly the atoms or molecules in a substance are connected.
” Phase changes are generally taught in chemistry classes. However, because the calorimetry and heating curves topics were moved from chemistry to physics in the Massachusetts Curriculum Frameworks starting in 2016, it is useful to review them here.
“In this section, the term “molecules” is used to refer to the particles that make up a substance. In chemistry, a molecule is a group of atoms that are covalently bonded together, and a substance can be made of individual atoms, molecules, crystals, or other types of particles. In these notes, the term “particles” is preferred, but “molecules” is used in this section because it conjures the impression of particles that are attached or bonded together in some way. This gives most students a reasonably correct picture of entities that are firmly attached to each other and cannot be pulled apart by physical means.
* Phase changes are generally taught in chemistry classes. However, because the calorimetry and heating curves topics were moved from chemistry to physics in the Massachusetts Curriculum Frameworks starting in 2016, it is useful to review them here.
+ In this section, the term “molecules” is used to refer to the particles that make up a substance. In chemistry, a molecule is a group of atoms that are covalently bonded together, and a substance can be made of individual atoms, molecules, crystals, or other types of particles. In these notes, the term “particles” is preferred, but “molecules” is used in this section because it conjures the impression of particles that are attached or bonded together in some way. This gives most students a reasonably correct picture of entities that are firmly attached to each other and cannot be pulled apart by physical means.
solid: molecules are rigidly connected. A solid has a definite shape and a definite volume.
liquid: molecules are loosely connected; bonds are continuously forming and breaking. A liquid has a definite volume, but not a definite shape.
gas: molecules are not connected. A gas has neither a definite shape nor a definite volume. Gases will expand to fill whatever space they occupy.
plasma: the system has enough heat to remove electrons from atoms, which means the system is comprised of charged particles moving very rapidly.
phase change: when an object or substance changes from one phase to another through gaining or losing heat.
Breaking bonds requires energy. Forming bonds releases energy. This is true for the intermolecular bonds that hold a solid or liquid together as well as for chemical bonds.
As you probably know from experience, you need to add energy to turn a solid to a liquid (melt it), or to turn a liquid to a gas (boil it).
- This is why evaporation causes cooling-because the system (the water) needs to absorb heat from its surroundings in order to make the change from a liquid to a gas (vapor).
- This is also why lids keep drinks hot. The lid is a barrier which significantly reduces the amount of evaporation.
- When you perspire, the water absorbs heat from you in order to evaporate, which cools you off.
It is less obvious that energy is released when a gas condenses or a liquid freezes.
- Ice in your ice tray needs to give off heat in order to freeze. (Your freezer needs to remove that heat in order to make this happen.)
- Burns from steam are much more dangerous than burns from water, because the steam releases a large amount of heat (which is absorbed by your body) as it condenses.
States of Matter
The following table shows interactions between the molecules and some observable properties for solids, liquids and gases. (The table includes heating curves, which will be discussed in more detail later in the next section, Heating Curves starting on page 219. For now, understand that a heating curve shows how the temperature changes as heat is added. Notice in particular that the temperature stays constant during melting and boiling.)
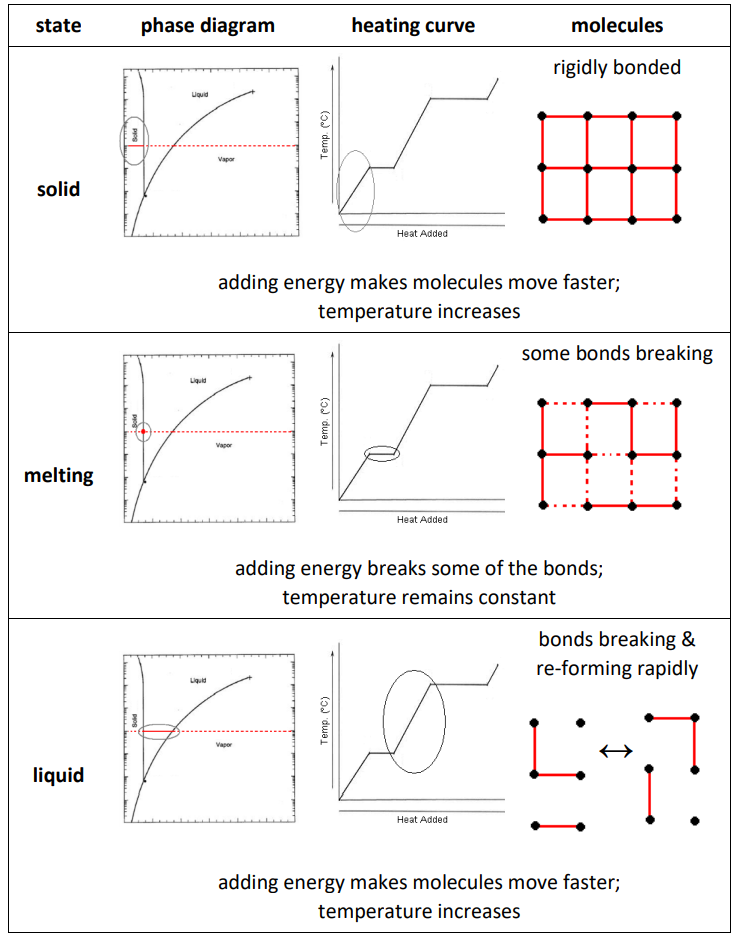
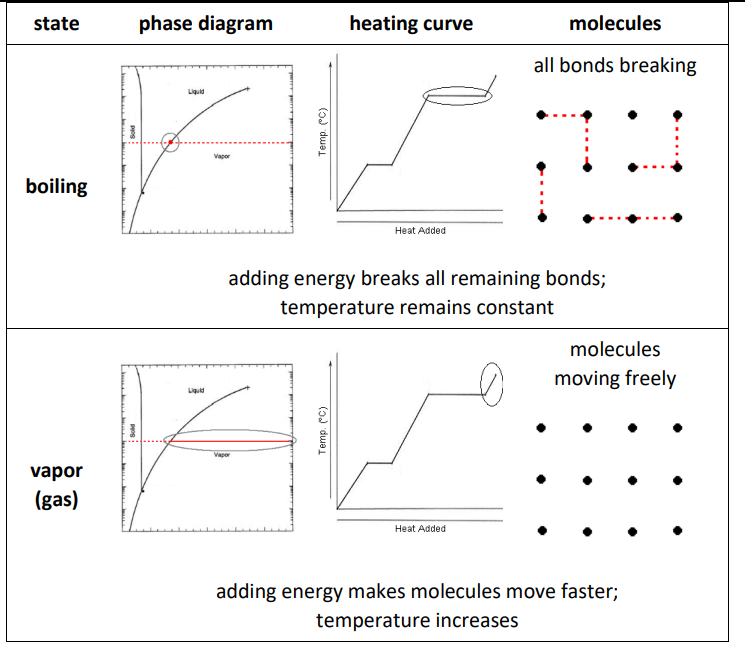
Note that because liquids are continually forming and breaking bonds, if a liquid molecule at the surface breaks its bonds with other liquids, it can “escape” from the attractive forces of the other liquid molecules and become a vapor molecule. This is how evaporation happens at temperatures that are well below the boiling point of the liquid
Phase Changes \& Heating Curves*
Notes:
phase: a term that relates to how rigidly the atoms or molecules in a substance are connected.
solid: molecules are rigidly connected. A solid has a definite shape and volume.
liquid: molecules are loosely connected-bonds are continuously forming and breaking. A liquid has a definite volume, but not a definite shape.
gas: molecules are not connected. A gas has neither a definite shape nor a definite volume. Gases will expand to fill whatever space they occupy.
plasma: the system has enough heat to remove electrons from atoms, which means the system is comprised of particles with rapidly changing charges.
phase change: when an object or substance changes from one phase to another through gaining or losing heat.
” Heating curves are usually taught in chemistry classes. However, the topic was moved from chemistry to physics in the Massachusetts Curriculum Frameworks starting in 2016.
Breaking bonds requires energy. Forming bonds releases energy. This is true for the bonds that hold a solid or liquid together as well as for chemical bonds (regardless of what previous teachers may have told you!)
I.e., you need to add energy to turn a solid to a liquid (melt it), or to turn a liquid to a gas (boil it). Energy is released when a gas condenses or a liquid freezes. (E.g., ice in your ice tray needs to give off heat in order to freeze. Your freezer needs to remove that heat in order to make this happen.)
The reason evaporation causes cooling is because the system (the water) needs to absorb heat from its surroundings (e.g., your body) in order to make the change from a liquid to a gas (vapor). When the water absorbs heat from you and evaporates, you have less heat, which means you have cooled off.
Calculating the Heat of Phase Changes
heat of fusion $\left(\Delta H_{f u s}\right)$ (sometimes called “latent heat” or “latent heat of fusion”): the amount of heat required to melt one kilogram of a substance. This is also the heat released when one kilogram of a liquid substance freezes. For example, the heat of fusion of water is $334 \frac{\mathrm{J}}{\mathrm{g}}$. The heat required to melt a sample of water is therefore:
$
Q=m \Delta H_{f u s}=m\left(334 \frac{\jmath}{g}\right)
$
heat of vaporization $\left(\Delta H_{\text {vap }}\right)$ : the amount of heat required to vaporize (boil) one kilogram of a substance. This is also the heat released when one kilogram of a gas condenses. For example, the heat of vaporization of water is $2260 \frac{\mathrm{J}}{\mathrm{g}}$. The heat required to boil a sample of water is therefore:
$
Q=m \Delta H_{\text {vap }}=m\left(2260 \frac{\jmath}{g}\right)
$
heating curve: a graph of temperature vs. heat added. The following is a heating curve for water:
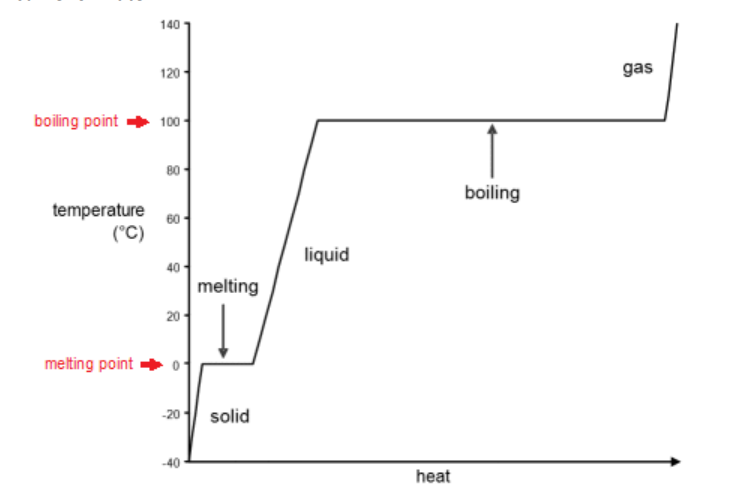
In the “solid” portion of the curve, the sample is solid water (ice). As heat is added, the temperature increases. The specific heat capacity of ice is $2.11 \frac{\mathrm{J}}{\mathrm{g} \cdot \mathrm{c} \mathrm{C}}$, so the heat required is:
$
Q_{\text {solid }}=m C \Delta T=m\left(2.11 \frac{\mathrm{J}}{\mathrm{g}^{\circ} \mathrm{C}}\right) \Delta T
$
In the “melting” portion of the curve, the sample is a mixture of ice and water. As heat is added, the ice melts, but the temperature remains at $0^{\circ} \mathrm{C}$ until all of the ice is melted. The heat of fusion of ice is $334 \frac{\mathrm{J}}{\mathrm{g}}$, so the heat required is:
$
Q_{m e l t}=m \Delta H_{f u s}=m\left(334 \frac{\jmath}{g}\right)
$
In the “liquid” portion of the curve, the sample is liquid water. As heat is added, the temperature increases. The specific heat capacity of liquid water is $4.181 \frac{\mathrm{J}}{\mathrm{g} \cdot \mathrm{\circ} \mathrm{C}}$, so the heat required is:
$
Q_{\text {liquid }}=m C \Delta T=m\left(4.181 \frac{\mathrm{J}}{\mathrm{g}^{\circ} \mathrm{C}}\right) \Delta T
$
In the “boiling” portion of the curve, the sample is a mixture of water and water vapor (steam). As heat is added, the water boils, but the temperature remains at $100^{\circ} \mathrm{C}$ until all of the water has boiled. The heat of vaporization of water is $2260 \frac{\mathrm{J}}{\mathrm{g}}$, so the heat required is:
$
Q_{\text {melt }}=m \Delta H_{\text {vap }}=m\left(2260 \frac{\jmath}{g}\right)
$
In the “gas” portion of the curve, the sample is water vapor (steam). As heat is added, the temperature increases. The specific heat capacity of steam is approximately $2.08 \frac{\mathrm{J}}{\mathrm{g} \cdot \mathrm{C}}$. (This is at $100^{\circ} \mathrm{C}$; the specific heat capacity of steam decreases as the temperature increases.) The heat required is:
$
Q_{g a s}=m C \Delta T=m\left(2.08 \frac{\jmath}{\mathrm{g}^{\circ} \mathrm{C}}\right) \Delta T
$
Steps for Solving Heating Curve Problems
A heating curve problem is a problem in which a substance is heated across a temperature range that passes through the melting and/or boiling point of the substance, which means the problem includes heating or cooling steps and melting/freezing or boiling/condensing steps.
1. Sketch the heating curve for the substance over the temperature range in question. Be sure to include the melting and boiling steps as well as the heating steps.
2. From your sketch, determine whether the temperature range in the problem passes through the melting and/or boiling point of the substance.
3. Split the problem into:
a. Heating (or cooling) steps within each temperature range.
b. Melting or boiling (or freezing or condensing) steps.
4. Find the heat required for each step.
a. For the heating/cooling steps, use the equation $Q=m C \Delta T$.
b. For melting/freezing steps, use the equation $Q=m \Delta H_{f u s}$.
c. For boiling/condensing steps, use the equation $Q=m \Delta H_{\text {vap }}$.
5. Add the values of $Q$ from each step to find the total.
Sample Problem
Q: How much heat would it take to raise the temperature of $15.0 \mathrm{~g}$ of $\mathrm{H}_2 \mathrm{O}$ from $-25.0^{\circ} \mathrm{C}$ to $+130.0^{\circ} \mathrm{C} ?$
Answer/Explanation
A: The $\mathrm{H}_2 \mathrm{O}$ starts out as ice. We need to:
1. Heat the ice from $-25.0^{\circ} \mathrm{C}$ to its melting point $\left(0^{\circ} \mathrm{C}\right)$.
2. Melt the ice.
3. Heat the water up to its boiling point (from $0^{\circ} \mathrm{C}$ to $100^{\circ} \mathrm{C}$ ).
4. Boil the water.
5. Heat the steam from $100^{\circ} \mathrm{C}$ to $130^{\circ} \mathrm{C}$.
6. Add up the heat for each step to find the total.
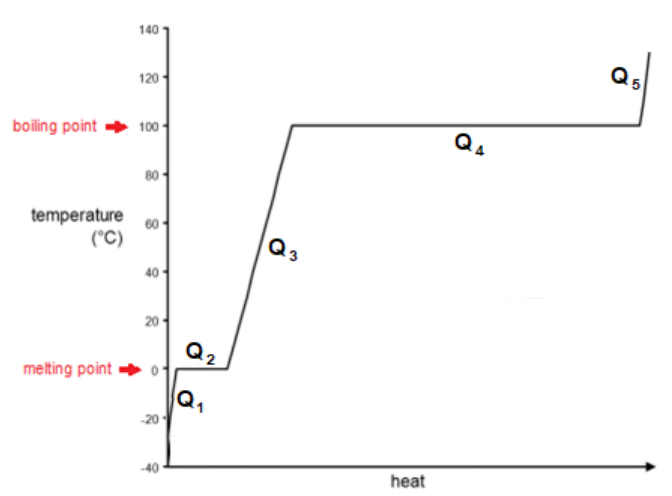
1. heat solid: $Q_1=m C \Delta T=(15)(2.11)(25)=791.25 \mathrm{~J}$
2. melt ice: $Q_2=m \Delta H_{f u s}=(15)(334)=5010 \mathrm{~J}$
3. heat liquid: $Q_3=m C \Delta T=(15)(4.181)(100)=6270 \mathrm{~J}$
4. boil water: $Q_4=m \Delta H_{\text {vap }}=(15)(2260)=33900 \mathrm{~J}$
5. heat gas: $Q_5=m C \Delta T=(15)(2.08)(30)=936 \mathrm{~J}$
6. $Q=Q_1+Q_2+Q_3+Q_4+Q_5$
$
Q=791+5010+6270+33900+936=46910 \mathrm{~J}
$
Thermal Expansion
Notes:expand: to become larger
contract: to become smaller
thermal expansion: an increase in the length and/or volume of an object caused by a change in temperature.
When a substance is heated, the particles it is made of move farther and faster. This causes the particles to move farther apart, which causes the substance to expand.
Solids tend to keep their shape when they expand. (Liquids and gases do not have a definite shape to begin with.)
A few materials are known to contract with increasing temperature over specific temperature ranges. One well-known example is liquid water, which contracts as it heats from $0^{\circ} \mathrm{C}$ to $4^{\circ} \mathrm{C}$. (Water expands as the temperature increases above $4^{\circ} \mathrm{C}$.)
Thermal Expansion of Solids and Liquids
Thermal expansion is quantified in solids and liquids by defining a coëfficient of thermal expansion. The changes in length and volume are given by the equation:
Length: $\Delta L=\alpha L_i \Delta T$
Volume: $\Delta V=\beta V_i \Delta T$
where:
$\Delta L=$ change in length $(\mathrm{m}) \quad L_i=$ initial length $(\mathrm{m})$
$\alpha=$ linear coëfficient of thermal expansion $\left({ }^{\circ} \mathrm{C}^{-1}\right)$
$\Delta V=$ change in volume $\left(\mathrm{m}^3\right) \quad V_i=$ initial volume $\left(\mathrm{m}^3\right)$
$\beta=$ volumetric coëfficient of thermal expansion $\left({ }^{\circ} \mathrm{C}^{-1}\right)$
$\Delta T=$ temperature change $\left({ }^{\circ} \mathrm{C}\right)$
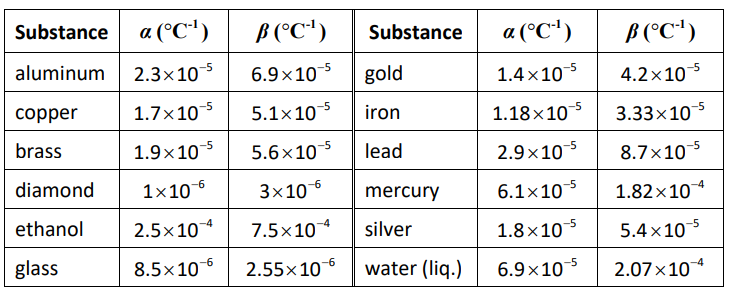
Values of $\alpha$ and $\beta$ at $20^{\circ} \mathrm{C}$ for some solids and liquids:

expansion joint: a space deliberately placed between two objects to allow room for the objects to expand without coming into contact with each other.
Bridges often have expansion joints in order to leave room for sections of the bridge to expand or contract without damaging the bridge or the roadway.
Railroad rails are sometimes welded together in order to create a smoother ride, which enables high-speed trains to use them. Unfortunately, if expansion joints are not placed at frequent enough intervals, thermal expansion can cause the rails to bend and buckle, resulting in derailments:

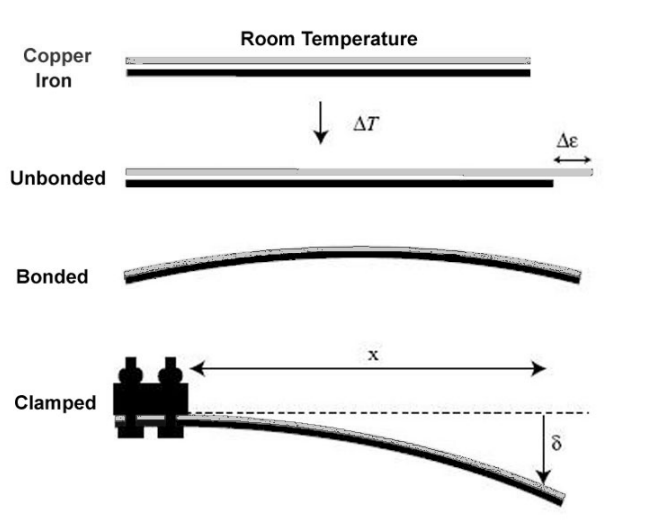
bimetal strip: a strip made from two metals with different coëfficients of thermal expansion that are bonded together. When the strip is heated or cooled, the two metals expand or contract different amounts, which causes the strip to bend. When the strip is returned to room temperature, the metals revert back to their original lengths
Sample Problems:
Q: Find the change in length of an $0.40 \mathrm{~m}$ brass rod that is heated from $25^{\circ} \mathrm{C}$ to $980^{\circ} \mathrm{C}$.
Answer/Explanation
A: For brass, $\alpha=1.9 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}$.
$
\begin{aligned}
& \Delta L=\alpha L_i \Delta \mathrm{T} \\
& \Delta L=\left(1.9 \times 10^{-5}\right)(0.40)(955) \\
& \Delta L=0.0073 \mathrm{~m}
\end{aligned}
$
Thermal Expansion of Gases
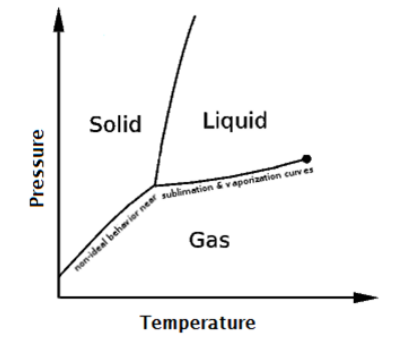
ideal gas: a gas that behaves as if each molecule acts independently, according to kinetic-molecular theory. Most gases behave ideally except at temperatures and pressures near the vaporization curve on a phase diagram. (I.e., gases stop behaving ideally when conditions are close to those that would cause the gas to condense to a liquid or solid.)
For an ideal gas, the change in volume for a change in temperature (provided that the pressure and number of molecules are kept constant) is given by Charles’ Law:
$
\frac{V_1}{T_1}=\frac{V_2}{T_2}
$
where $V_1$ and $T_1$ are the initial volume and temperature, and $V_2$ and $T_2$ are the final volume and temperature, respectively. Volume can be any volume unit (as long as it is the same on both sides), but temperature must be in Kelvin.