Topics covered in this chapter:
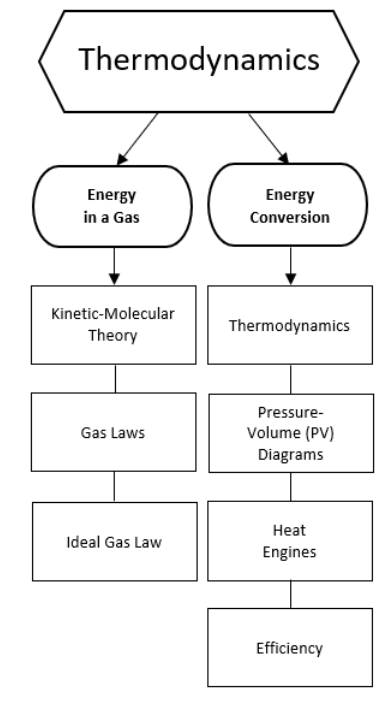
Kinetic-Molecular Theory
Notes:
In your chemistry classes, you learned about matter, including its composition, structure, and changes that it can undergo. In physics, we are interested in matter to the extent that it can be used to bring objects or energy in contact with each other and transfer forces, energy or momentum from one object or collection of objects to another. This chapter is about gases and using properties of gases to convert between mechanical and thermal energy.
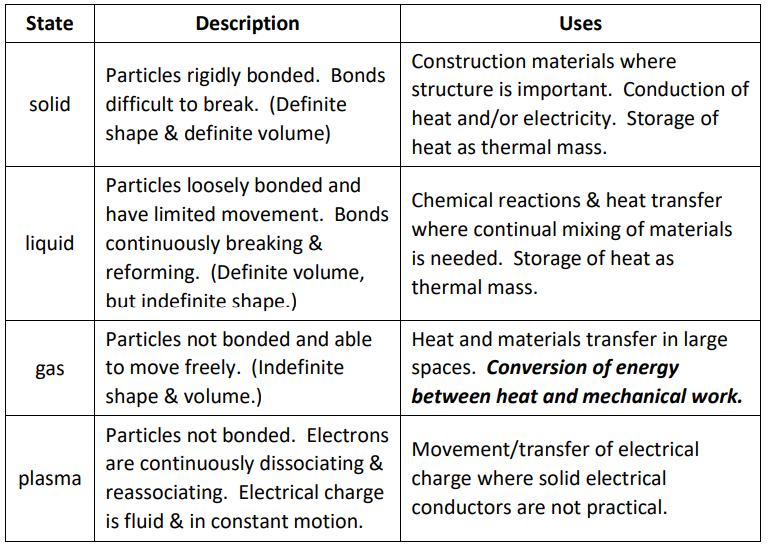
Properties of Different States of Matter
Kinetic-Molecular Theory (KMT)
- Kinetic-Molecular Theory (KMT) is a theory, developed by James C. Maxwell and Ludwig Boltzmann, that predicts the behavior of gases by modeling them as moving molecules. (“kinetic” = “moving”.) The theory states that:
- Gases are made of very large numbers of molecules ${ }^*$
- Molecules are constantly moving (obeying Newton’s laws of motion), and their speeds are constant
- Molecules are very far apart compared with their diameter
- Molecules collide with each other and walls of container in elastic collisions
- Molecules behaving according to KMT are not reacting ${ }^{+}$or exerting any other forces (attractive or repulsive) on each other.
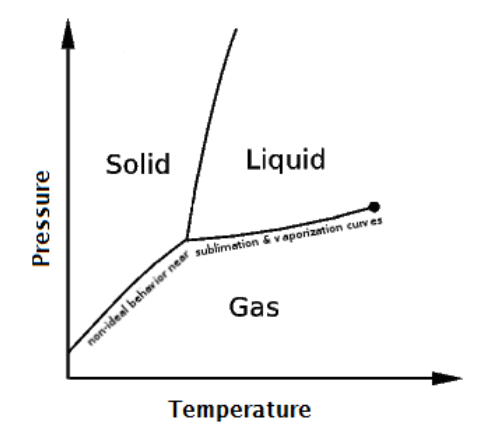
ideal gas: a gas whose molecules behave according to KMT. Most gases are ideal under some conditions (but not all). In general, gases behave ideally when they are not close to the solid or liquid regions of the phase diagram for the substance.
real gas: a gas whose molecules do not behave according to KMT. This can occur with all gases, most commonly at temperatures and pressures that are close to the solid or liquid regions of the phase diagram for the substance.
“In this chapter we will use the terms “particle” and “molecule” interchangeably, with apologies to chemists.
‘ Of course, reactions can occur, but chemical reactions are part of collision theory, which is separate from KMT.
Measurable Properties of Gases
All gases have the following properties that can be measured:
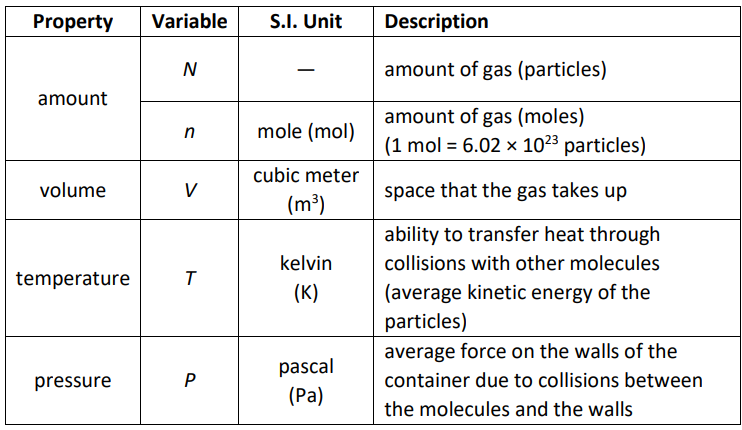
Notes about calculations:
- Moles are based on the definition that 1 mole $=6.02214076 \times 10^{23}$ particles . 1 mole was originally the number of carbon atoms in exactly 12 grams of carbon-12, such that the molar mass of a substance is the same number of grams as the average atomic mass of one atom in atomic mass units. This definition persisted, despite the fact that the base mass unit of the MKS system is the kilogram.
- Temperature must be absolute, which means you must use Kelvin. A temperature of 0 in a gas laws calculation can only mean absolute zero.
- Pressures must be absolute. (For example, you can’t use a tire gauge because it measures “gauge pressure,” which is the difference between atmospheric pressure and the pressure inside the tire.) A pressure of 0 in a gas laws calculation can only mean that there are no molecules colliding with the walls.
Other Common Units - Volume can be measured in liters (L) or milliliters $(\mathrm{mL})$. $1 \mathrm{~m}^3=1000 \mathrm{~L}$ and $1 \mathrm{~L}=1000 \mathrm{~mL}$
- Pressure can be measured in many different units. $1 \mathrm{~atm}=101325 \mathrm{~Pa}=14.696 \mathrm{psi}=760 \mathrm{~mm} \mathrm{Hg}=29.92 \mathrm{in} . \mathrm{Hg}$ $1 \mathrm{bar}=100000 \mathrm{~Pa}=100 \mathrm{kPa} \approx 1 \mathrm{~atm}$
Other Common Units
- Volume can be measured in liters (L) or milliliters $(\mathrm{mL})$. $1 \mathrm{~m}^3=1000 \mathrm{~L}$ and $1 \mathrm{~L}=1000 \mathrm{~mL}$
- Pressure can be measured in many different units.
$
\begin{aligned}
& 1 \mathrm{~atm}=101325 \mathrm{~Pa}=14.696 \mathrm{psi}=760 \mathrm{~mm} \mathrm{Hg}=29.92 \mathrm{in} . \mathrm{Hg} \\
& 1 \mathrm{bar}=100000 \mathrm{~Pa}=100 \mathrm{kPa} \approx 1 \mathrm{~atm}
\end{aligned}
$
Gas Laws
Notes:
ideal gas: a gas that behaves as if each molecule acts independently, according to kinetic-molecular theory. Specifically, this means the molecules are far apart, and move freely in straight lines at constant speeds. When the molecules collide, the collisions are perfectly elastic, which means they bounce off each other with no energy or momentum lost. (See the section on Kinetic-Molecular Theory, starting on page 240.)
Avogadro’s Principle
In 1811, Italian physicist Amedeo Avogadro (whose full name was Lorenzo Romano Amedeo Carlo Avogadro di Quaregna e di Cerreto) published the principle that equal volumes of an ideal gas at the same temperature and pressure must contain equal numbers of particles.

If the pressure and temperature are constant, then for an ideal gas:
$
\begin{array}{ll}
\frac{V_1}{N_1}=\frac{V_2}{N_2} & \frac{V_1}{n_1}=\frac{V_2}{n_2} * \\
\text { (particles) } & \text { (moles) }
\end{array}
$
Although Avogadro’s principle was originally stated in terms of particles ( $N$ ) of gas, it is almost always more convenient to work with moles $(n)$.
(Note that by convention, gas laws use subscripts ” 1 ” and ” 2 ” instead of ” 0 ” for initial no subscript for final.)
” Avogadro’s principle is usually stated $\frac{n_1}{V_1}=\frac{n_2}{V_2}$. I have inverted it in these notes so that the quantities in the numerator and denominator are the same as the quantities in the numerator and denominator of the combined gas law.
Boyle’s Law
In 1662, British physicist and chemist Robert Boyle published his findings that the pressure and volume of a gas were inversely proportional.
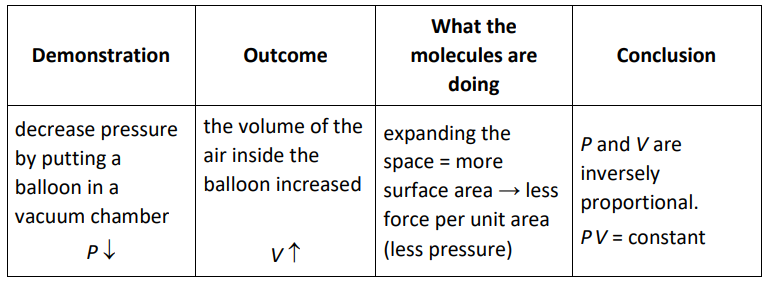
Therefore, if the temperature and the number of particles of gas are constant, then for an ideal gas:
$
P_1 V_1=P_2 V_2
$
Charles’ Law
In the 1780 s, French physicist Jacques Charles discovered that the volume and temperature of a gas were directly proportional.
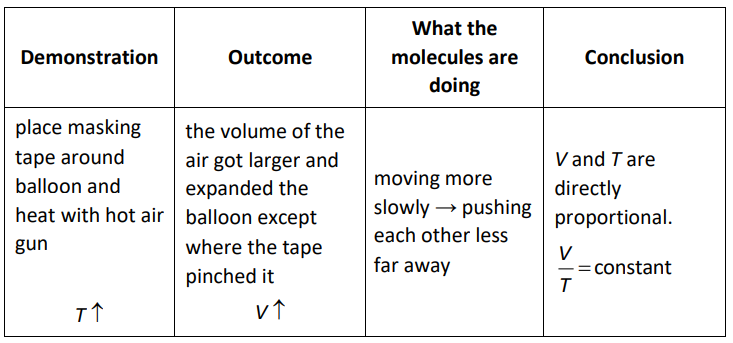
If pressure and the number of particles are constant, then for an ideal gas:
$\frac{V_1}{T_1}=\frac{V_2}{T_2}$
Gay-Lussac’s Law
In 1702, French physicist Guillaume Amontons discovered that there is a relationship between the pressure and temperature of a gas. However, precise thermometers were not invented until after Amontons’ discovery so it wasn’t until 1808, more than a century later, that French chemist Joseph Louis Gay-Lussac confirmed this law mathematically. The pressure law is most often attributed to Gay-Lussac, though some texts refer to it as Amontons’ Law.
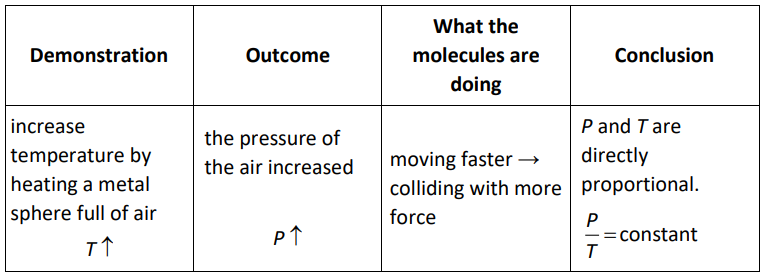
If volume and the number of particles are constant, then for an ideal gas:
$
\frac{P_1}{T_1}=\frac{P_2}{T_2}
$
The Combined Gas Law
We can combine each of the above principles. When we do this (keeping $P$ and $V$ in the numerator and $n$ (or $N$ ) and $T$ in the denominator for consistency), we get following relationship for an ideal gas:
$
\begin{array}{crl}
\frac{P_1 V_1}{n_1 T_1}= & \frac{P_2 V_2}{n_2 T_2}=\text { constant } & \frac{P_1 V_1}{N_1 T_1}=\frac{P_2 V_2}{N_2 T_2}=\text { constant } \\
\text { using moles } & \text { using particles }
\end{array}
$
Note, however, that in most situations where we want to calculate properties of a gas, the number of moles or particles remains constant. This means $n_1=n_2$ or $N_1=N_2$, and we can cancel it from the equation. This gives:
$
\frac{P_1 V_1}{T_1}=\frac{P_2 V_2}{T_2}
$
The above equation is called the “combined gas law”, which is used to solve most “before/after” problems involving ideal gases.
When using the combined gas law, any quantity that is not changing may be cancelled out of the equation. (If a quantity is not mentioned in the problem, you can assume that it is constant and may be cancelled.)
For example, suppose a problem doesn’t mention anything about temperature. That means $T$ is constant and you can cancel it. When you cancel $T$ from both sides of the combined gas law, you get:
$
\frac{P_1 V_1}{T_1}=\frac{P_2 V_2}{T_2^{\prime}} \text { which simplifies to } P_1 V_1=P_2 V_2 \text { (Boyle’s Law) }
$
Solving Problems Using the Combined Gas Law
You can use this method to solve any “before/after” gas law problem:
1. Determine which variables you have
2. Determine which values are initial (\#1) vs. final (\#2).
3. Start with the combined gas law and cancel any variables that are explicitly not changing or omitted (assumed not to be changing).
4. Substitute your numbers into the resulting equation and solve. (Make sure all initial and final quantities have the same units, and don’t forget that temperatures must be in Kelvin!)
Note: because quantities appear on both sides of the equation, it is not necessary to use S.I. units when solving problems using the combined gas law. It is, however, important to use the same units for the same quantity on both sides of the equation.
Sample problem:
Q: A gas has a temperature of $25^{\circ} \mathrm{C}$ and a pressure of $1.5 \mathrm{bar}$. If the gas is heated to $35^{\circ} \mathrm{C}$, what will the new pressure be?
Answer/Explanation
A: 1. Find which variables we have.
We have two temperatures $\left(25^{\circ} \mathrm{C}\right.$ and $\left.35^{\circ} \mathrm{C}\right)$, and two pressures ( $1.5 \mathrm{bar}$ and the new pressure that we’re looking for).
2. Find the action being done on the gas (“heated”). Anything that was true about the gas before the action is time ” 1 “, and anything that is true about the gas after the action is time ” 2 “.

3. Set up the formula. We can cancel volume $(V)$, because the problem doesn’t mention it:
$
\frac{P_1 V_1}{T_1}=\frac{P_2 V_2}{T_2} \text { which gives us } \frac{P_1}{T_1}=\frac{P_2}{T_2} \text { (Gay-Lussac’s Law) }
$
4. Plug in our values and solve:
$
\frac{1.5 \mathrm{bar}}{298 \mathrm{~K}}=\frac{P_2}{308 \mathrm{~K}} \rightarrow P_2=1.55 \mathrm{bar}
$
Ideal Gas Law
Notes:
ideal gas: a gas that behaves according to Kinetic-Molecular Theory (KMT).
When we developed the combined gas law, before we cancelled the number of moles or particles, we had the equations: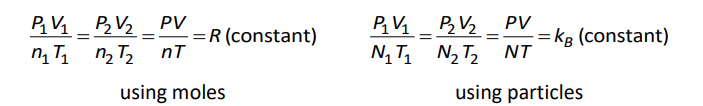
where $n$ is the number of moles of gas, and $N$ is the number of gas particles. One mole is $6.02 \times 10^{23}$ particles, which means $N=\left(6.02 \times 10^{23}\right) n$
Because $P, V, n$ and $T$ are all of the quantities needed to specify the conditions of an ideal gas, this expression must be true for any ideal gas under any conditions. If $V$ is in $\mathrm{m}^3, P$ is in $\mathrm{Pa}, n$ is in moles, and $T$ is in Kelvin, then:
$
R=8.31 \frac{\mathrm{J}}{\mathrm{mol} \cdot \mathrm{K}} \text { and } k_B=1.38 \times 10^{-23} \frac{\mathrm{J}}{\mathrm{K}}
$
$R$ is called “the gas constant,” and $k_{\mathrm{B}}$ is Boltzmann’s constant.
We can rearrange $\frac{P V}{n T}=R$ and $\frac{P V}{N T}=k_B$ to get the ideal gas law in its familiar form:
$
P V=n R T \quad \text { and } \quad P V=N k_B T
$
Other Values of $\mathbf{R}$
The purpose of the gas constant $R$ is to convert the quantity $n T$ from units of mol. $\mathrm{K}$ to units of pressure $\times$ volume. This constant can have different values, depending on the units that it needs to cancel:
$
\begin{aligned}
& \mathrm{R}=0.0821 \frac{\mathrm{L} \cdot \mathrm{atm}}{\mathrm{mol} \cdot \mathrm{K}} \\
& \mathrm{R}=8.31 \frac{\mathrm{J}}{\mathrm{mol} \cdot \mathrm{K}} \equiv 8.31 \frac{\mathrm{m}^3 \cdot \mathrm{Pa}}{\mathrm{mol} \cdot \mathrm{K}} \equiv 8.31 \frac{\mathrm{L} \cdot \mathrm{kPa}}{\mathrm{mol} \cdot \mathrm{K}} \equiv 8.31 \times 10^{-3} \frac{\mathrm{kJ}}{\mathrm{mol} \cdot \mathrm{K}} \\
& \mathrm{R}=62.4 \frac{\mathrm{L} \cdot \mathrm{torr}}{\mathrm{mol} \cdot \mathrm{K}} \\
& \mathrm{R}=1.987 \frac{\mathrm{cal}}{\mathrm{mol} \cdot \mathrm{K}} \equiv 1.987 \frac{\mathrm{BTU}}{\mathrm{lb}-\mathrm{mol} \cdot{ }^{\circ} \mathrm{R}}
\end{aligned}
$
Use of non-S.I. units, such as atm or torr, is more common in chemistry. In this course, we will use the S.I. units of $\mathrm{m}^3$ for volume and Pa for pressure. The unit $\mathrm{Pa} \cdot \mathrm{m}^3$ is equivalent to a joule.
Solving Problems Using the Ideal Gas Law
If a gas behaves according to the ideal gas law, simply substitute the values for pressure, volume, number of moles (or particles), and temperature into the equation. Be sure your units are correct (especially that temperature is in Kelvin), and that you use the correct constant, depending on whether you know the number of particles or the number of moles of the gas.
Sample Problem:
A $3.50^n \mathrm{~mol}$ sample of an ideal gas has a pressure of $120000 \mathrm{P}$ Pa and a temperature of $35^{\circ} \mathrm{C}$. What is its volume?
$T \rightarrow K$ (v)
Answer/Explanation
Answer:
$
\begin{array}{ll}
P=120000 \mathrm{~Pa} & n=3.50 \mathrm{~mol} \\
V=V & R=8.31 \frac{\mathrm{J}}{\mathrm{mol} \cdot \mathrm{K}} \\
T & =35^{\circ} \mathrm{C}+273=308 \mathrm{~K}
\end{array}
$
Then we substitute these numbers into the ideal gas law and solve:
$
\begin{gathered}
P V=n R T \\
V=\frac{n R T}{P}=\frac{(3.50)(8.31)(308)}{120000}=0.0747 \mathrm{~m}^3
\end{gathered}
$
Real Gases
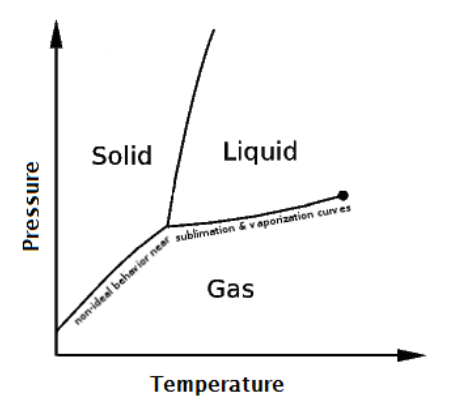
As stated previously, when the temperature and pressure of a gas are close to the solid or liquid regions of the phase diagram for the substance, gases start to exhibit non-ideal behaviors. Recall the following definition of a real gas:
real gas: a gas whose molecules do not behave according to kinetic-molecular theory (KMT). This occurs most commonly at temperatures and pressures that are close to the solid or liquid regions of the phase diagram for the substance.
In the late $19^{\text {th }}$ century, the Dutch physicist Johannes van der Waals published a correction to the ideal gas law that can be applied to real gases.
The van der Waals Equation applies correction factors to the pressure and volume terms in the equation:
$
\left(P+a \frac{n^2}{V^2}\right)(V-n b)=n R T
$
in this equation, the constants $a$ and $b$ are properties specific to a gas and must be looked up or determined experimentally.
The corrected pressure term $\left(P+a \frac{n^2}{V^2}\right.$ instead of $\left.P\right)$ is because molecules attract each other slightly at low pressures, but repel each other when they are forced close together. This repulsion acts like additional pressure.
The corrected volume term $(V-n b$ instead of $V)$ term is because the ideal gas law assumes that the molecules are far enough apart that we do not need to consider the volumes of the molecules themselves as part of the volume of their container. As the molecules are brought closer together, we have to subtract the space taken up by $n$ moles of molecules from the available volume.
You will not need to solve problems using the van der Waals equation in this course.
Thermodynamics
Notes:
thermodynamics: the study of heat-related (thermal) energy changes (dynamics)
Thermodynamics is an application of the law of conservation of energy. In Physics 1 , we studied changes between gravitational potential energy and kinetic energy. Thermodynamic changes involve the same principle; the details and the equations, however, are quite different.
As was the case with gas laws, the topic of thermodynamics is studied by both chemists and physicists. Chemists tend to be more concerned with the heat produced and consumed by chemical changes and reactions. Physicists tend to be more concerned with the conversion between thermal energy (regardless of how it is produced) and other forms of energy, particularly mechanical.
thermal equilibrium: if two systems “A” and “B” are in thermal equilibrium, heat is transferred from A to B at the same rate as heat is transferred from B to A.

temperature: a measure of the average kinetic energy of the particles in a substance. (K)
$K_{\text {ave. }}=\frac{1}{2} m v_{\text {ave. }}^2=\frac{3}{2} k_B T$
where:
$
\begin{aligned}
K_{\text {ave. }} & =\text { average kinetic energy }(\mathrm{J}) \\
m & =\text { mass of a particle }(\mathrm{kg}) \\
M & =\text { molar mass (mass of one mole of particles) }\left(\frac{\mathrm{kg}}{\mathrm{mol}}\right) \\
v_{\text {ave. }} & =\text { average velocity of a particle }\left(\frac{\mathrm{m}}{\mathrm{s}}\right) \\
k_B & =\text { Boltzmann’s constant }=1.38 \times 10^{-23} \frac{\mathrm{J}}{\mathrm{K}} \\
T & =\text { temperature }(\mathrm{K})
\end{aligned}
$
The factor of $\frac{3}{2}$ is because there is an equal probability of a collision between particles in the $x-, y$-, and $z$-directions, and $(3)\left(\frac{1}{2}\right)=\frac{3}{2}$.
root mean square velocity $\left(v_{\text {rms }}\right)$ : the geometric mean (average) velocity of a particle. $\left(\frac{m}{s}\right)$ The rms velocity is derived by solving $\frac{1}{2} m v_{a v e .}^2=\frac{3}{2} k_B T$ for the average velocity:
$
v_{r m s}=\sqrt{v_{a v e:}^2}=\sqrt{\frac{3 k_B T}{m}}=\sqrt{\frac{3 R T}{M}}
$
internal energy $\left(U^*\right):$ the total thermal energy of a system due to the kinetic energy of its particles.
If the kinetic energy of a single particle is $K_{a v e .}=\frac{3}{2} k_B T$, then the total kinetic energy in a system that has $N$ particles would be:
$
U=N K_{\text {ave. }}=\frac{3}{2} N k_B T
$
Because it is generally unwieldy to perform calculations for systems with large numbers of particles, it is more convenient to use moles. Substituting $n R$ for $N k_B$ gives the equation for the internal energy of a system that has $n$ moles of particles:
$
U=\frac{3}{2} n R T
$
Similarly, a chanqe in internal energy $(\Delta U)$ is related to the corresponding change in temperature $(\Delta T)$ :
$
\Delta U=\frac{3}{2} n R \Delta T\left(=\frac{3}{2} N k_B \Delta T\right)
$
heat $(Q)$ : thermal energy transferred into or out of a system. (J)
work $(W)$ : mechanical energy (such as the application of a force over a distance) transferred into or out of a system. (J)
The work that a gas can do comes from its ability to move an object by applying a force on it as it expands. If the pressure is constant:
$
\begin{gathered}
W=F d=F \Delta x \\
P=\frac{F}{A} \rightarrow F=P A \\
\therefore W=(P A) \Delta x \\
\Delta V=A \Delta x \\
\therefore W=P \Delta V
\end{gathered}
$
If a gas does work by expanding, the energy is transferred from the gas (the system) to the object that the gas is pushing against (the surroundings). This means that when the volume increases ( $\Delta V$ is positive), energy is leaving the system ( $W$ is negative). Conversely, if work is done to compress a gas, energy is entering the system in order to compress the gas ( $W$ is positive), and the volume decreases ( $\Delta V$ is negative). This means that $W$ and $P \Delta V$ must have opposite signs, which gives the equation:
$
W=-P \Delta V
$
assuming that pressure is constant.
Laws of Thermodynamics
The laws of thermodynamics describe the behavior of systems with respect to changes in heat energy.
For historical reasons, the laws are numbered from $0-3$ instead of 1-4.
0. If a system is at thermal equilibrium, every component of the system has the same temperature. (“You have to play the game.”)
1. Heat always flows from a region of higher internal energy to a region of lower internal energy. Because internal energy is directly proportional to temperature, this is equivalent to saying that heat flows from a region of higher temperature to a region of lower temperature. This means you can’t get more heat out of a system than you put in. (“You can’t win.”)
2. In almost every change, some energy is irretrievably lost to the surroundings. Entropy is a measure of this “lost” energy. The entropy of the universe is always increasing, which means on any practical scale, you always get out less energy than you put in. (“You can’t break even.”)
3. Conservation of energy always applies. In any closed system, the total energy (internal energy + entropy + work) remains constant. If energy was “lost,” it turned into an increase in entropy. (“You can’t get out of the game.”)
Zeroth Law (or Zero Law)
The zeroth law says that if you have multiple systems in thermal equilibrium (the heat transferred from “A” to ” $B$ ” is equal to the heat transferred from ” $\mathrm{B}$ ” to ” $\mathrm{A}$ “), then the systems must have the same temperature. The consequences of this are:
- If we have three (or more) systems ” $\mathrm{A}$, ” ” $\mathrm{B}$,” and ” $\mathrm{C}$,” and $\mathrm{A}$ is in thermal equilibrium with $B$, and $B$ is in thermal equilibrium with $C$, this means that $A$, $B$, and $C$ must all have the same temperature, and $A$ is therefore in thermal equilibrium with $C$. (This is akin to the transitive property of equality in mathematics.)
- If an object with a higher temperature (a “hotter” object) is in contact with an object with a lower temperature (a “colder” object), heat will flow from the object with higher temperature to the object with lower temperature until the temperatures are the same (the objects are in thermal equilibrium).
First Law
Consider an isolated system-i.e., a system where heat and other forms of energy cannot enter nor leave the system. This system is doing no work, but it has internal energy.
Internal energy is similar to potential energy-it is a property of a system that is not doing work currently, but has the potential to do work in the future.
According to the First Law, the internal energy of a system increases $(\Delta U>0)$ if heat is added to the system $(Q>0)$ or if work is done on the system $(W>0)$. The internal energy decreases if the system gives off heat or the system does work on its surroundings.
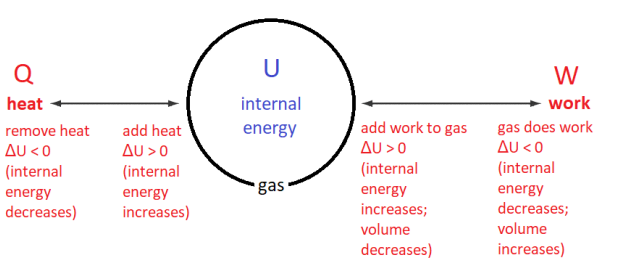
In equation form, the First Law looks like this:
$
\Delta U=Q+W^*
$
The First Law is simply the law of conservation of energy-the change in internal energy comes from the heat added to or removed from the system combined with the work done on or by the system.
Combining the First Law with the definition of internal energy gives:
$
\Delta U=\frac{3}{2} n R \Delta T=Q+W
$
” Some textbooks define work exclusively as work done by the system on the surroundings (i.e., energy leaving the system). Using this definition would reverse the sign of $W$ in the equation, giving:
$
\Delta U=Q-W
$
FSample Problem:
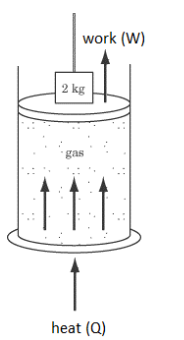
Q: A cylinder containing a gas has a piston with a weight on top. The combined mass of the piston plus the weight is $2 \mathrm{~kg}$. Heat is added, and the piston rises a distance of $0.2 \mathrm{~m}$. If this process occurred while keeping the temperature of the gas in the container constant, how much heat was added to the gas?
Answer/Explanation
A: No gas was added to the system, and the temperature does not change. Because $\Delta U=\frac{3}{2} n R \Delta T$, if $\Delta T=0$, that means $\Delta U=0$
Work was done by the system to raise the piston. Using the work equation from physics 1 :
$
W=\Delta U=m g \Delta h=(2)(10)(0.2)=4 \mathrm{~J}
$
Note that the work is done by the system on the surroundings. This means work is going out of the system.
We use positive numbers for energy coming into the system (from the surroundings), and negative numbers for work leaving the system (going into the surroundings).
This means the work is $-4 \mathrm{~J}$.
Applying the First law:
$
\begin{aligned}
\Delta U & =Q+W \\
0 & =Q+(-4) \\
Q & =+4 \mathrm{~J}
\end{aligned}
$
Second Law
The Second law tells us that heat energy cannot flow from a colder system to a hotter one unless work is done on the system. This is why your coffee gets cold and your ice cream melts.
One consequence of this law is that no machine can work at $100 \%$ efficiency; all machines generate some heat, and some of that heat is always lost to the surroundings.
Entropy
Because energy must be conserved, we have to account for energy that still exists, but has “gotten lost” (“escaped” or “spread out”) and is no longer usable by the system. Energy that has spread out and cannot be recovered is called entropy.
For example, when an egg falls to the floor and breaks, gravitational potential energy is converted to a combination of internal energy (the measurable increase in the temperature of the egg), and entropy (heat energy that is radiated to the environment and “lost”). Over time, the internal energy in the egg is also radiated to the environment and “lost” as the egg cools off. Ultimately, all of the gravitational potential energy ends up converted to entropy, which is the heat energy that is dissipated and cannot be recovered.
Entropy is sometimes called “disorder” or “randomness”, but in the thermodynamic sense this is not correct. The entropy of your room is a thermodynamic property of the heat energy in your room, not a commentary on the amount of dirty laundry on the floor!
Whenever heat is transferred from an object with a higher temperature to an object with a lower temperature, the heat “spreads out” as it warms the colder object. The amount of energy that goes into this “spread” is called entropy.
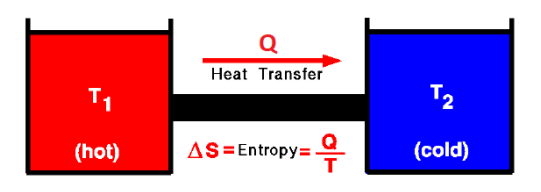
If the heat is transferred in a way that is completely reversible (which is impossible and would take an infinite amount of time), then you would be able to recover the energy that was converted to entropy when transferring it back to the hotter object. We call this fictitious heat “reversible heat,” denoted $Q_{\text {rev. }}$.
$
\Delta S=\frac{Q_{\text {rev }}}{T}
$
Real energy transfers that take place in finite amounts of time can never recover all of the energy that was turned into entropy. This means the actual increase in entropy is always more than the amount that would occur in a reversible process:
$
\Delta S=\frac{Q_{\text {rev }}}{T} \geq \frac{Q}{T}
$
In other words, the energy that is lost to entropy by transfer of an amount of heat $Q$ would be $\frac{Q}{T}$ for a completely reversible process (where $Q=Q_{\text {rev }}$ ), and more than that for any real process.
Because actual heat transfer in a finite amount of time cannot be completely reversible, some heat is lost to the surroundings and the actual entropy change is always greater than the actual heat change at a given temperature. The concept of a reversible process is an idealization that represents the maximum amount of work that could theoretically be extracted from the process.
A consequence of the Second Law is that the entropy of the universe is always increasing.
In physics, there is a hierarchy of thinking. Conservation of energy, conservation of momentum, and the Second Law are at the top of the hierarchy. Just as special relativity tells us that time, distance and mass all need to be changeable in order to maintain conservation of energy and momentum, the Second Law explains why time cannot move backwards-to do so would require a decrease in the entropy of the universe.
Third Law
The Third Law tells us that in an isolated system, the total energy of the system must be constant. (An isolated system is a system for which it is not possible to exchange energy with the surroundings.) This makes intuitive sense; because energy must be conserved, if no energy can be added or taken away, then the total energy cannot change.
Thermodynamic Quantities and Equations
Because energy is complex and exists in so many forms, there are many thermodynamic quantities that can be calculated in order to quantify the energy of
different portions of a system. The following is a list of some of the more familiar ones:
Selected Thermodynamic Quantities
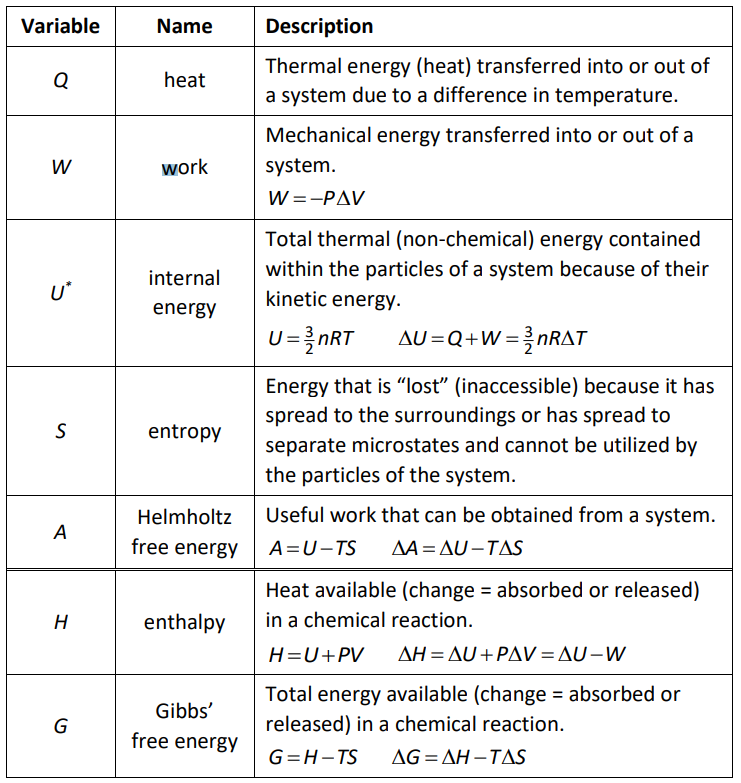
Thermodynamics Equations Used in This Course
Most of the thermodynamics problems encountered in this course are applications of the following equations

$W=-\int P d V=-P \Delta V \quad$ work vs. change in volume (at constant pressure)
Of course, many problems require you to combine these equations, such as:
$
\Delta U=\frac{3}{2} n R \Delta T=Q+W
$
and, if pressure is constant, $\int P d V=P \int d V=P \Delta V^*$ :
$
-W=P \Delta V=n R \Delta T
$
The problems that you will encounter will involve a change in a measurable state variable (pressure, volume and/or temperature). To solve these problems, you will need to:
1. Determine whether the change involves heat transfer, work, and/or a change in internal energy.
2. Apply algebraic combinations of one or more of these equations to answer the question.
* If the pressure is changing, there is no way to calculate the work without using calculus. In this algebra-based course, we will limit ourselves to problems that can be solved without calculus.
Pressure-Volume (PV) Diagrams
Notes:
P-V diagram: a graph that shows changes in pressure vs. changes in volume.
Recall that:
$
W=-\int P d V
$
On a graph, the integral is the area “under the curve” (meaning the area between the curve and the $x$-axis).
Therefore, if we plot a graph of pressure vs. volume with pressure on the $y$-axis and volume on the $x$-axis, the integral would therefore be represented by the area between the curve (pressure) and the $x$-axis.
This means that the work done by a thermodynamic change equals the area under a p-Vgraph. ${ }^*$
” While the above explanation requires calculus, we will limit ourselves to areas that can be calculated using simple geometry equations. Note that some of these will result in situations that would not realistically be achievable in the “real world”.
In the following example, suppose that a gas is compressed from $3 \mathrm{~m}^3$ to $1 \mathrm{~m}^3$ at a pressure of $1 \mathrm{~Pa}$. (A pressure of $1 \mathrm{~Pa}$ is much smaller than you would encounter in any real problem; these numbers were chosen to keep the math simple.)
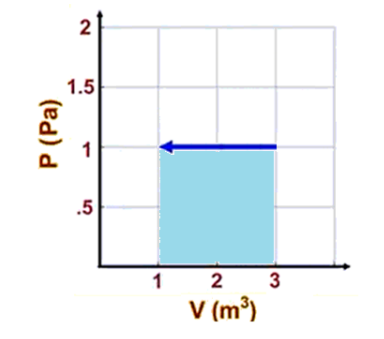
The pressure is $P=1 \mathrm{~Pa}$, and the change in volume is $\Delta V=-2 \mathrm{~m}^3$. Because pressure is constant, we can use $W=-P \Delta V=-(1)(-2)=+2 \mathrm{~J}$.
$P \Delta V$ is the area under the graph. Because it is a rectangular region, the area is the base of the rectangle times the height. The base is $2 \mathrm{~m}^3$ and the height is $1 \mathrm{~Pa}$, which gives an area of $2 \mathrm{~J}$.
Note that the arrow showing the change points to the left, which indicates that the volume is decreasinq. Because work must be put into the gas in order to compress it, this means that the work done on the gas will be positive. This is where the negative sign comes from. $W=-P \Delta V$ means that:
- if work is done on the gas (work is positive), the gas is compressed and the change in volume is therefore negative.
- If work is done by the gas on the surroundings (work is negative), the gas expands and the change in volume is therefore positive.
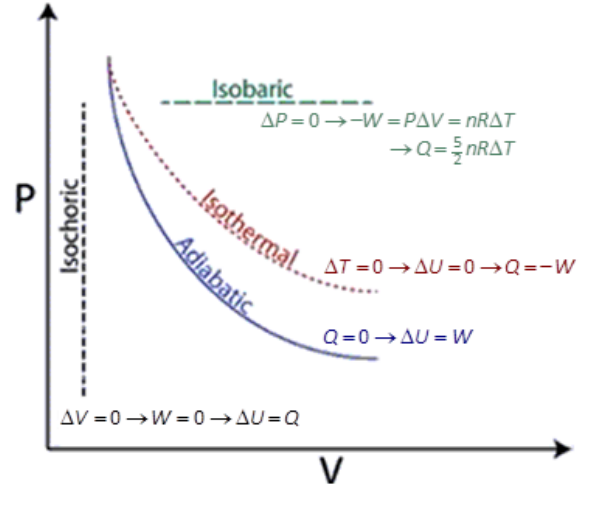
We will look at the effects of changes in pressure vs. volume in four types of pressure-volume changes:
- isochoric (constant volume)
- isothermal (constant temperature)
- adiabatic (no heat loss)
- isobaric (constant pressure).
Isochoric
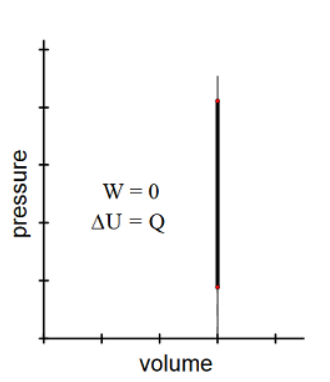
From Greek “iso” (same) and “khoros” (volume).
An isochoric change is one in which volume remains constant, but pressure and temperature may vary.
An example is any rigid, closed container, such as a thermometer.
Because the volume is not changing, there is no way for the gas to push against anything. This means the gas cannot do work, so $W=0$.
$
\begin{aligned}
& W=0 \\
& \Delta U=Q+W^n \\
& \Delta U=Q
\end{aligned}
$
Another way to think of a constant volume change is that if you add heat to a rigid container of gas, none of the energy can be converted to work, so all of it must be converted to an increase in internal energy (i.e., an increase in temperature).
Isothermal
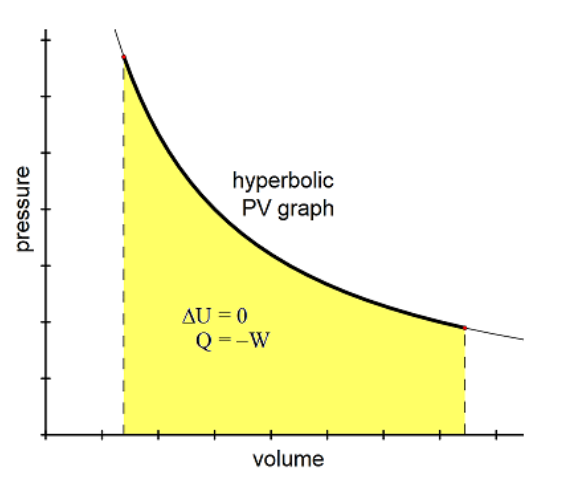
Constant temperature.
From Greek “iso” (same) and “thermotita” (heat). An isothermal change is one in which temperature remains constant, but pressure and volume may vary.
An example is any “slow” process, such as breathing out through a wide open mouth.
Because $\Delta T=0$ (definition of isothermal), this means
$
\Delta U=\frac{3}{2} N k_B \Delta T^n=0
$
Further, because:
$
\begin{aligned}
\Delta U & =Q+W=0 \\
Q & =-W
\end{aligned}
$
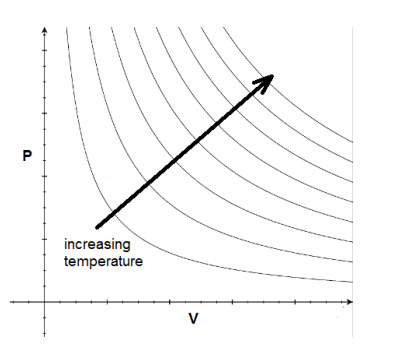
The $\mathrm{P}-\mathrm{V}$ curve for an isothermal process is called an isotherm. Note that isotherms are hyperbolas, i.e., they are solutions to the equation $P V=$ constant. You may recall that allowing pressure and volume to change while keeping temperature constant is represented by Boyle’s Law: $P_1 V_1=P_2 V_2$
As temperature increases, the isotherm moves farther away from the origin.
Adiabatic
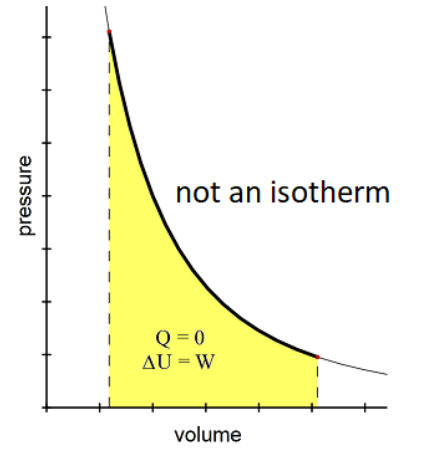
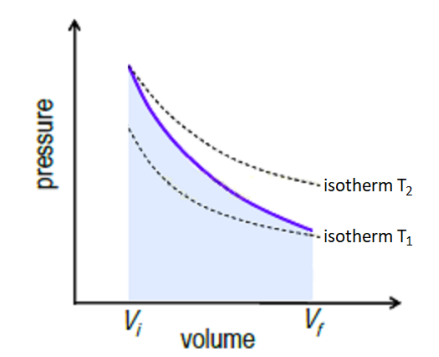
An adiabatic process is one in which there is no heat exchange with the environment.
An example is any “fast” process, such as forcing air out through pursed lips or a bicycle tire pump.
Because the definition of an adiabatic process is one for which $Q=0$, this means:
$
\begin{aligned}
Q & =0 \\
\Delta U & =Q+W \\
\Delta U & =W
\end{aligned}
$
Note that adiabatic expansion (sudden increase in volume without time for heat transfer) results in a decrease in temperature, and adiabatic compression (sudden decrease in volume without time for heat transfer) results in an increase in temperature.
Isobaric
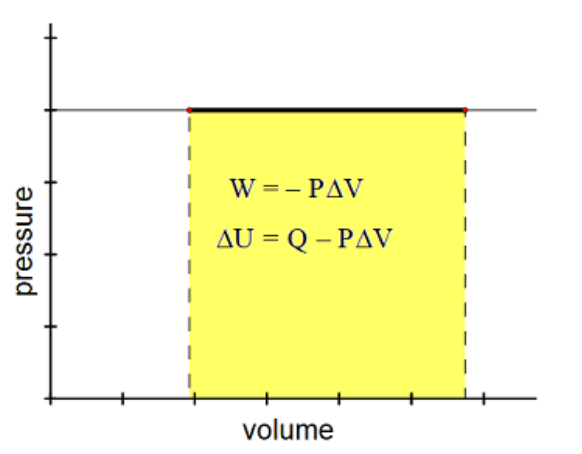
From Greek” iso” (same) and “baric” (heavy). An isobaric change is one in which pressure remains constant, but volume and temperature may vary.
Some examples include a weighted piston, a flexible container in earth’s atmosphere, or a hot air balloon.
Isobaric changes involve changes in both $Q$ and $W$,
because to change the volume of a gas while keeping pressure constant, you need to add or remove heat, but the resulting change in volume means that work is being done.
$
\begin{aligned}
W & =-\Delta(P V)=-P \Delta V \\
\Delta U & =Q+W \\
\Delta U & =Q+(-P \Delta V) \\
\Delta U & =Q-P \Delta V
\end{aligned}
$
Adding $P \Delta V$ to both sides gives $Q=\Delta U+P \Delta V$
Now, because $\Delta U=\frac{3}{2} n R \Delta T$ and $P \Delta V=n R \Delta T=\frac{2}{2} n R \Delta T$, that means:
$
\begin{aligned}
& Q=\Delta U+P \Delta V \\
& Q=\frac{3}{2} n R \Delta T+\frac{2}{2} n R \Delta T \\
& Q=\frac{5}{2} n R \Delta T
\end{aligned}
$
This makes sense, because some of the heat is used to do the work of expanding the gas $(P \Delta V=n R \Delta T)$, and some of the heat is used to increase the temperature.
$
\left(\Delta U=\frac{3}{2} n R \Delta T\right)
$
If we wanted to compare all four processes on the same PV diagram, they would look like this:
Positive vs. Negative Work
In thermodynamics problems, whether work is represented by a positive or negative number depends on how the problem is stated.
Work done on the gas: a positive number means work is coming from the surroundings into the gas.
Work done $\underline{\boldsymbol{b} \boldsymbol{y}}$ the gas: a positive number means work is going from the gas out to the surroundings.
If the problem does not specify otherwise, the convention is to use a positive number to indicate work done on the gas.
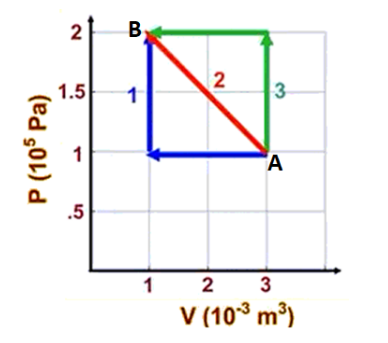
Sample Problem
Q: Calculate the work done as the pressure and volume of a gas are taken from
point A to point B along each of paths 1, 2, and 3.rem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Answer/Explanation
A: Process \#1 is first isobaric (constant pressure), then isochoric (constant volume).
For the isobaric part of the process:
$
\begin{aligned}
& W=-P \Delta V \\
& W=-\left(1 \times 10^5\right)\left(1 \times 10^{-3}-3 \times 10^{-3}\right) \\
& W=-\left(1 \times 10^5\right)\left(-2 \times 10^{-3}\right) \\
& W=2 \times 10^2=200 \mathrm{~J}
\end{aligned}
$
For the isochoric process, there is no change in volume, which means the gas does no work (because it cannot push against anything). Therefore $W=0$.
The total work for process \#1 is therefore $200 \mathrm{~J}$.
Notice that the work is equal to the area under the PV graph, which is a rectangular area with a base of $2 \times 10^{-3} \mathrm{~m}^3$ and a height of $1 \times 10^5 \mathrm{~Pa}$.
$
W=\left(1 \times 10^5\right)\left(2 \times 10^{-3}\right)=200 J
$
Note that because the arrow points to the left, this means the volume is decreasing. That means work is being done on the gas, which means the work is represented by a positive number. (We have to make this determination any time we use the graph to calculate the work.)
For process \#2, the area is the $200 \mathrm{~J}$ square that we calculated for process \#1 plus the area of the triangle above it, which is $\frac{1}{2} b h=\frac{1}{2}\left(2 \times 10^{-3}\right)\left(1 \times 10^5\right)=100 \mathrm{~J}$. Therefore, $200 \mathrm{~J}+100 \mathrm{~J}=300 \mathrm{~J}$.
For process \#3, the area under the curve is $W=\left(2 \times 10^5\right)\left(2 \times 10^{-3}\right)=400 \mathrm{~J}$.
Heat Engines
Notes:
heat engine: a device that turns heat energy into mechanical work.
A heat engine operates by taking heat from a hot place (heat source), converting some of that heat into work, and dumping the rest of the heat into a cooler reservoir (heat sink).
A large number of the machines we use-most notably cars-employ heat engines.
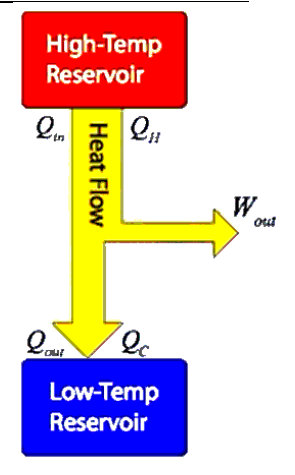
The basic principle of heat engine is the first law of thermodynamics (heat flows from a region of higher temperature to a region of lower temperature). Because heat is a form of energy, some of that energy can be harnessed to do work.
The law of conservation of energy tells us that all of the energy that we put into the heat engine must go somewhere. Therefore, the work done plus the heat that comes out must equal the heat we put in.
This means:
$
Q_{\text {in }}=Q_{\text {out }}+W_{\text {out }}
$
The above picture is easier to understand in the context of a PV diagram.
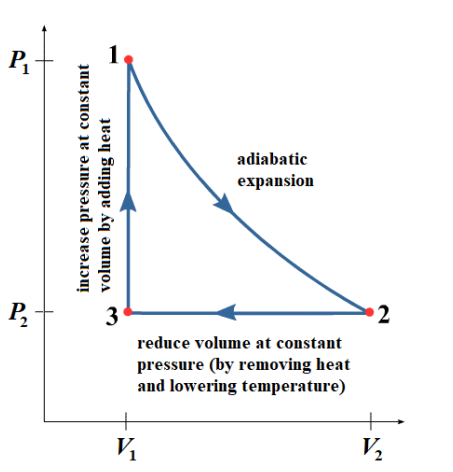
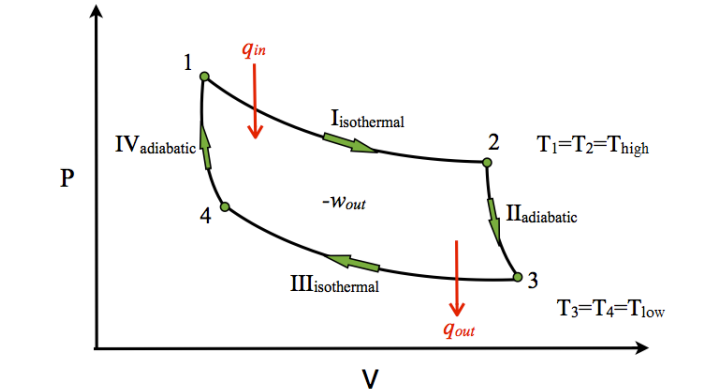
1. Starting from point $1\left(V_1, P_1\right)$, the gas is expanded adiabatically (without losing heat) to point $2\left(V_2, P_2\right)$. The area under the graph from point $1-2$ represents the work that is done by the gas ( $\left.W_{\text {out }}\right)$ as it expands and cools.
2. Ultimately, we need to get the gas back to point 1 so we can begin the cycle over again, but in a way that costs less work than we got out. There are many ways to accomplish this. In this example, the next step is to reduce the volume isobarically, by removing heat $\left(Q_{\text {out }}\right)$. (This is what the low temperature reservoir is for.) This results in a decrease in temperature as well as a decrease in volume, which gets us to point $3\left(V_1\right.$, $\left.P_2\right)$.
3. Now we increase the pressure to get from point $3\left(V_1, P_2\right)$ to point $1\left(V_1, P_1\right)$ by adding heat to the gas without letting the volume change. We do this by bringing the gas back to the high temperature reservoir so it can absorb the heat $\left(Q_{\text {in }}\right)$.
Heat Pumps
A heat pump is a device, similar to a heat engine, that “pumps” heat from one place to another. A refrigerator and an air conditioner are examples of heat pumps. A refrigerator uses a fluid (“refrigerant”) to transfer (or “pump”) heat from the inside of the refrigerator to the outside of the refrigerator (and into your kitchen).
This is why you can’t cool off the kitchen by leaving the refrigerator door openeven if you had a $100 \%$ efficient refrigerator (most refrigerators are actually only $20-40 \%$ efficient), all of the heat that you pumped out of the refrigerator is still in the kitchen!
A refrigerator works by the following process.
1. Work is put in to compress a refrigerant (gas). In most cases, the gas is compressed until it turns into a liquid, which means additional energy is stored in the phase change. This increases the temperature of the refrigerant to about $70^{\circ} \mathrm{C}$.
2. The refrigerant (now a liquid) passes through cooling coils on the back of the refrigerator. The liquid is cooled through convection by the air in the kitchen to about $25^{\circ} \mathrm{C}$
3. The refrigerant (still a liquid) is pumped to the inside of the refrigerator and allowed to expand to a gas adiabatically. Work comes out of the gas, and the temperature drops to about $-20^{\circ} \mathrm{C}$.
4. Heat is transferred via convection from the contents (the food) to the refrigerant.
5. The refrigerant (still a gas) is pumped out of the refrigerator, which brings us back to step 1.
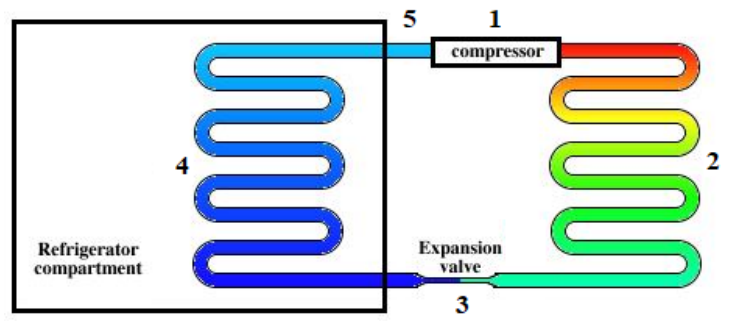
A heater can operate under the same principle, by putting the cooling coils inside the room and having the expansion (which cools the refrigerant) occur outside. Individual rooms in homes are sometimes heated and cooled by reversible heat pumps called “mini-splits”.
Heat Engines and PV Diagrams
On a PV diagram, a heat engine is any closed loop or cycle:
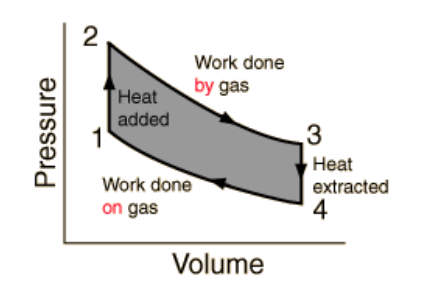
Recall that on a PV diagram, a curve that moves from left to right represents work done $\underline{b y}$ the gas on the surroundings. (Work is leaving the system, so $\Delta W<0$.) $\mathrm{A}$ curve that moves from right to left represents work done on the gas by the surroundings. (Work is entering the system so $\Delta W>0$.)
A heat engine is a clockwise cycle, which means more work is done going to the right than to the left, which means there is a net flow of work out of the system (i.e., the heat is being used to do work). A refrigerator is a counterclockwise cycle, in which more work is put in and more heat is taken out.
The Carnot cycle, named after the French physicist Nicolas Carnot, is the most efficient type of heat engine. The Carnot cycle, which uses only adiabatic (no heat loss) and isothermal processes, is the basis for heat pumps (including refrigerators and air conditioners) :
The internal combustion engine in a car is also a type of heat engine. The engine is called a “four-stroke” engine, because the piston makes four strokes (a back or forth motion) in one complete cycle. The four strokes are:
1. The piston moves down (intake), sucking a mixture of gasoline and air into the cylinder.
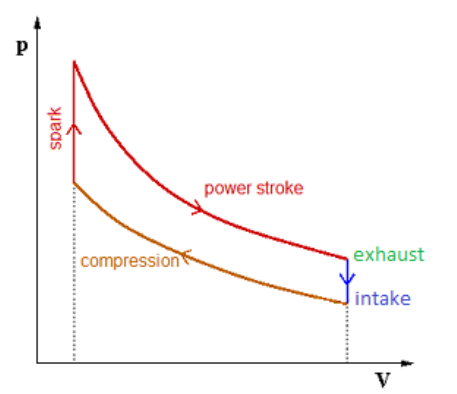
2. The piston moves up (compression), compressing the gases in the cylinder.
3. The spark plug creates a spark, which combusts the gases. This increases the temperature in the cylinder to approximately 250°C.
4. The gas expands (power stroke), which is the work that the engine provides to make the car go.
5. The piston raises again, forcing the exhaust gases out of the cylinder (exhaust).
Note that, at the end of the cycle, the gas is hotter than its original temperature. The hot gas from the cylinder is dumped out the exhaust pipe, and fresh (cool) gas and fuel is added. This is why the blue intake arrow on the right moves downwardthe intake is at a lower temperature (lower isotherm).
The energy to move the piston for the intake and exhaust strokes is provided by the power strokes of the other pistons.
This cycle-constant temperature compression, constant volume heating (spark), constant temperature expansion (power), and constant volume gas exchange (exhaust) is called the Otto cycle, named after Nikolaus August Otto, who used this type of heat engine to build the first commercially successful internal combustion engine.
Efficiency
Notes:
efficiency $(\eta)$ : the ratio of the energy consumed by a device or process to the energy output by the device or process.
Assume that a heat engine starts with a certain temperature, which means a certain internal energy $(U)$. The engine takes heat from a heat source at the incoming temperature $T_{i n}$, does work $(W)$, and exhausts heat at the higher temperature $T_{\text {out }}$. Assuming the internal energy of the machine itself stays constant, this means $\Delta U=0$. Therefore, from the First law:
$
\begin{aligned}
\Delta U & =0=\Delta Q-\Delta W \\
0 & =Q_{\text {in }}-Q_{\text {out }}-\Delta W \\
\Delta W & =Q_{\text {in }}-Q_{\text {out }}
\end{aligned}
$
A $100 \%$ efficient heat engine would turn all of the heat into work, and would exhaust no heat $\left(Q_{o u t}=0\right.$, which would mean $\left.\Delta W=Q_{i n}\right)$. Of course, real engines cannot do this, so we define efficiency, e, as the ratio of work out to heat in, i.e.:
$
e=\frac{\Delta W}{\Delta Q_{i n}}=\frac{\Delta Q_{i n}-\Delta Q_{\text {out }}}{\Delta Q_{i n}}=\frac{\Delta Q_{i n}}{\Delta Q_{i n}}-\frac{\Delta Q_{\text {out }}}{\Delta Q_{i n}}=1-\frac{\Delta Q_{\text {out }}}{\Delta Q_{i n}}
$
Because the engine is doing work, $\Delta W>0$, which means $0 \leq e \leq 1$. Furthermore, a consequence of the Second law is that some energy is always lost to the surroundings (entropy), which means $Q_{\text {out }}>0$ and therefore $0 \leq e<1$.
Sample Problem
Q: 80. J of heat is injected into a heat engine, causing it to do work. The engine then exhausts 20 . J of heat into a cool reservoir. What is the efficiency of the engine?
Answer/Explanation
A: $Q_{\text {in }}=80 \mathrm{~J}$ and $Q_{\text {out }}=20 \mathrm{~J}$. Therefore:
$
e=1-\frac{\Delta Q_{\text {out }}}{\Delta Q_{\text {in }}}=1-\frac{20}{80}=1-0.25=0.75
$
Because efficiency is usually expressed as a percentage, we would say that the engine is $75 \%$ efficient.
The following table gives energy conversion efficiencies for common devices and processes. In all of these cases, the “lost” energy is converted to heat that is given off to the surroundings.

You may notice that an electric heater is 100% efficient, because all of its energy is converted to heat. However, this does not mean that electric heat is necessarily the best choice for your home, because the power plant that generated the electricity is probably only 45% efficient.
Heating Efficiency
Heating efficiency is calculated in a similar way. The difference is that the energy produced by the heater is $Q_{\text {out }}$, which means:
$
\eta=\frac{Q_{\text {out }}}{Q_{i n}}=\frac{\text { usable heat out }}{\text { total energy in }}
$
“Usable heat out” means heat that is not lost to the environment. For example, if the boiler or furnace in your house is $70 \%$ efficient, that means $70 \%$ of the energy from the gas or oil that it burned was used to heat the steam, hot water or hot air that was used to heat your house. The other $30 \%$ of the energy heated the air in the boiler or furnace, and that heat was lost to the surroundings when the hot air went up the chimney.
Older boilers and furnaces (pre-1990s) were typically $70 \%$ efficient. Newer boilers and furnaces are around $80 \%$ efficient, and high-efficiency boilers and furnaces that use heat exchangers to collect the heat from the exhaust air before it goes up the chimney can be $90-97 \%$ efficient.
Efficiency of a Heat Pump
Carnot’s theorem states that the maximum possible efficiency of a heat pump is related to the ratio of the temperature of the heat transfer fluid (liquid or gas) when it enters the heat pump to the temperature when it exits:
$
\eta \leq 1-\frac{T_{\text {in }}}{T_{\text {out }}}
$
Note that the Carnot equation is really the same as the efficiency equation in the previous section. Recall that for heating or cooling a substance:
$
Q=m C \Delta T=m C\left(T_{\text {out }}-T_{\text {in }}\right)
$
The refrigerant is the same substance, which means $m C$ is the same for the input as for the output, and it drops out of the equation.
It is a little counter-intuitive that a higher temperature difference means the heat pump is more efficient, but you should think about the fact that the job of the heat pump is to move heat between one side and the other. In other words, the more heat you pump into the refrigerant, the higher its temperature will be when it leaves the system, and therefore the more efficiently the pump is moving heat.
Conversely, if $T_{\text {out }}=T_{\text {in }}$, then the heat pump is not moving any heat and the efficiency is zero.
Sample Problem
Q: Refrigerant enters a heat pump at $20 .{ }^{\circ} \mathrm{C}\left(293 \mathrm{~K}\right.$ ) and exits at $300 .{ }^{\circ} \mathrm{C}(573 \mathrm{~K})$. What is the Carnot efficiency of this heat pump?
Answer/Explanation
A: Carnot’s equation states that:
$
\begin{aligned}
& \eta=1-\frac{T_{\text {in }}}{T_{\text {out }}}=1-\frac{293}{573} \\
& \eta=1-0.51=0.49
\end{aligned}
$
I.e., this heat pump is $49 \%$ efficient.Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.