Question
Four charge \(+\mathrm{q},+\mathrm{q},-\mathrm{q}\) and \(-\mathrm{q}\) are placed respectively at the corners \(\mathrm{A}, \mathrm{B}, \mathrm{C}\) and D of a square of side (a), arranged in the given order. Calculate the intensity of electric field at the center of the square where \(Q\) is a charge.
▶️Answer/Explanation
Ans:
Consider the problem
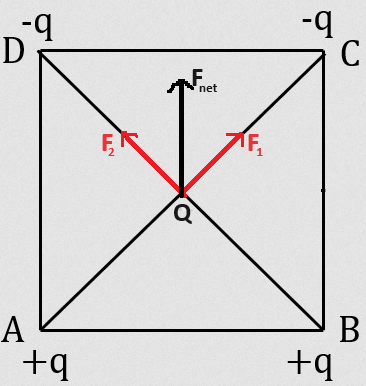
\(\mathrm{F}_1\) by \(-\mathrm{q}\) and \(+\mathrm{q}\) on \(\mathrm{Q}\) charge
\[
\begin{aligned}
& \mathrm{F}_1=\frac{\mathrm{kQq}}{\left(\frac{\mathrm{a}}{\sqrt{2}}\right)^2}+\frac{\mathrm{kQq}}{\left(\frac{\mathrm{a}}{\sqrt{2}}\right)^2} \\
& =\frac{4 \mathrm{kQq}}{\mathrm{a}^2} \mathrm{~N}
\end{aligned}
\]
And
\(F_2\) by \(-q\) and \(+q\) on \(Q\) charge
\[
\begin{aligned}
& F_2=\frac{k Q q}{\left(\frac{a}{\sqrt{2}}\right)^2}+\frac{k Q q}{\left(\frac{a}{\sqrt{2}}\right)^2} \\
& =\frac{4 k Q q}{a^2} \mathrm{~N} \\
& F_1=F_2=\frac{4 k Q q}{a^2} N
\end{aligned}
\]
Now F Resultant
\[
\begin{aligned}
& =\sqrt{\left(F_1\right)^2+\left(F_2\right)^2+2 F_1 F_2 \cos 90^{\circ}} \\
& =\sqrt{2} \mathrm{~F} \\
& =\sqrt{2}\left(\frac{4 \mathrm{kQq}}{\mathrm{a}^2}\right) \\
& =4 \sqrt{2} \frac{\mathrm{kQq}}{\mathrm{a}^2}
\end{aligned}
\]
Question
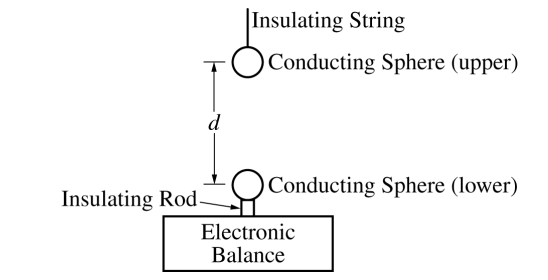
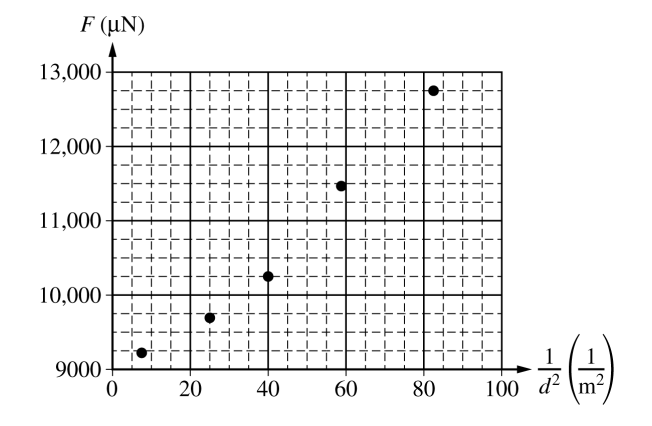
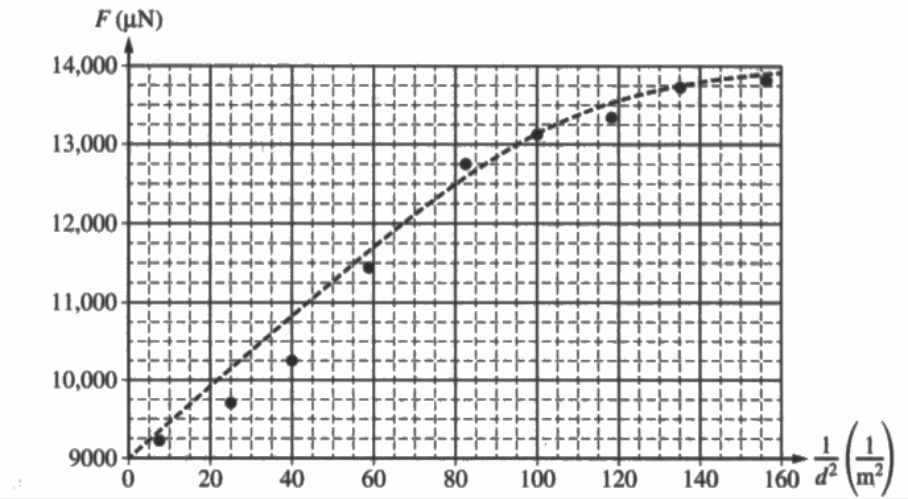
Students perform an experiment to study the force between two charged objects using the apparatus shown above, which contains two identical conducting spheres. The upper sphere is attached to an insulating string, which can be used to move the sphere downward. The lower sphere sits on an insulating rod, which is on an electronic balance. The electronic balance is zeroed before the lower sphere and insulating rod are in place. For the first trial, a charge of Q is placed on each sphere and then the upper sphere is slowly moved downward. The students measure the distance d between the centers of the spheres and the magnitude F of the force that appears on the electronic balance. The recorded data are shown on the graph of F as a function of \(\frac{1}{d^{2}}\) shown below.
(a)
i. Draw a line that represents the best fit to the points shown.
ii. Use the graph to calculate the charge Q.
iii. On the graph on the previous page, draw a circle around the data point that was taken when the distance between the centers of the spheres was the least.
iv. Determine the distance between the centers of the spheres for the data point indicated above.
v. What physical quantity does the vertical intercept represent?
Justify your answer.
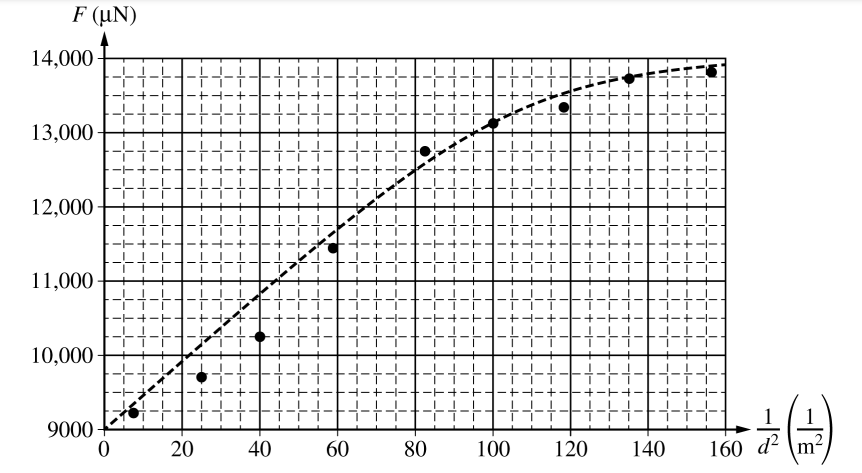
The experiment is extended by collecting additional data points, which appear on the right side of the graph shown above. The new data points do not follow the linear pattern seen with the first points. The group of students tries to explain this discrepancy.
(b) One student suspects that charge is slowly leaking off the top sphere. Could this explain the discrepancy?
____ Yes _____ No
Justify your answer.
(c) A second student suspects that the excess charges have rearranged themselves, polarizing the spheres.
i. On the circles representing the spheres below, use a single “ ”+ sign on each sphere to represent the locations of highest concentration of the excess positive charges.
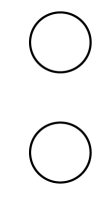
ii. Explain how this rearrangement could be responsible for the discrepancy.
(d) A third student suggests that the experiment be modified so that the top sphere is given a negative charge that is equal in magnitude to the positive charge given to the bottom sphere.
i. On the circles representing the spheres below, use a single “ ”+ sign on the bottom sphere to represent the location of highest concentration of the excess positive charges. Use a single “ ” − sign on the top sphere to represent the location of the highest concentration of the excess negative charges.
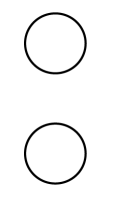
ii. For a separation distance equal to that of the data point indicated in part (a)(iii), would the magnitude of the force reading with spheres of opposite charges be greater than, less than, or equal to the magnitude of the force reading with spheres of the same charges?
_____ Greater than _____ Less than _____ Equal to
Justify your answer.
Answer/Explanation
Ans:
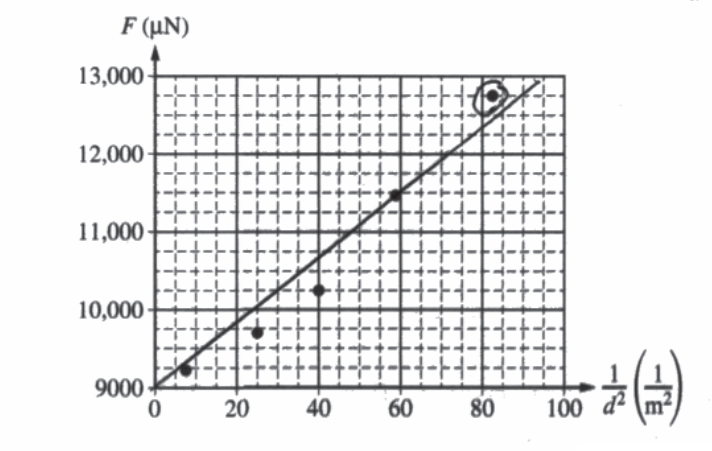
(a) ii.
\(slope = \frac{100.500\mu N}{60\frac{1}{m^{2}}}=0.69 Nm^{2}\)
\(Q = \sqrt{\frac{Fd^{2}}{k}}=\sqrt{\frac{slope}{k}}=8.76 \mu C\)
iv.
\(\frac{1}{d^{2}}= 81\frac{1}{m^{2}}\) d = 0.111 m
v.
the weight of the lower sphere and insulating rod
The vertical intercept represents the force when the top sphere is infinitely for away, so the only force acting on the scale is the weight of the lower sphere and insulating rod.
(b)
X Yes
If the top sphere’s charge decreases, then the force also decreases, as seen in the graph because of the curve of best fit falling below a straight line. Therefore, leaking charge could explain the discrepancy.
(c) i.

ii.
X Less than
With opposite charges, the electric force and weight force oppose each other, which decreases the magnitude of the force when compared to the same charges.
Question
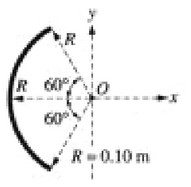
A rod of uniform linear charge density \(\lambda =+1.5 \times 10^{-5}\) C/m is bent into an arc of radius R = 0.10 m. The arc is placed with its center at the origin of the axes shown above.
a. Determine the total charge on rod.
b. Determine the magnitude and direction of the electric field at the center O of the arc.
c. Determine the electric potential at point O.
A proton is now placed at point O and held in place. Ignore the effects of gravity in the rest of this problem.
d. Determine the magnitude and direction of the force that must be applied in order to keep the proton at
rest.
e. The proton is now released. Describe in words its motion for a long time after its release.
Answer/Explanation
Ans:
a. The total charge is \(q=\lambda L = \lambda (2 \piR/3)=3.1 \times 10^{-6}\) C
b. \(E=kQ/R^2\), all of the charge is equidistant, but we must take direction into account. The y components will
cancel so we only need to consider the x (horizontal) component from each infinitesimal element dq = λR dθ
\(E=\int_{120}^{240}\frac{kdq}{R^2}cos \theta d\theta = \int_{120}^{240}\frac{kd \lambda R}{R^2}cos \theta d \theta =\int_{120}^{240}\frac{k\lambda}{R}cos \theta d\theta=\frac{k\lambda}{R}sin \theta |^{240}_{120}=2.3 \times 10^6 N/C\)
To the right
c. \(V=kQ/R=2.8 \times 10^5\) V ( all charge is equidistant from point O)
d. \(F=qE=3.7 \times 10^{-13}N\)
e. The proton moves off to the right, but as the force decreases the proton’s acceleration decreases, all the while
speeding up to the right asymptotic to some value