Focus Question: How does current move through a conductor?
- Current is any motion of charge within a conductor. It can be expressed at the amount of charge flowing through a cross section of a conductor per unit time:
$
I=\frac{d Q}{d t}
$
Example A: How much charge passes through a conductor in from $\mathrm{t}=0 \mathrm{~s}$ to $=5.0 \mathrm{~s}$ if the current is given by $I(t)=0.5 \sin (0.2 t)$ ?
Answer/Explanation
$
\begin{aligned}
& I=\frac{d Q}{d t} \rightarrow Q=\int I d t=\int_0^5 .5 \sin (.2 t) \\
& \rightarrow Q=\left(-\left.2.5 \cos (.2 t)\right|_0 ^5=1.15 \mathrm{C}\right.
\end{aligned}
$
Drift Velocity
- Current can be expressed in terms of drift velocity.
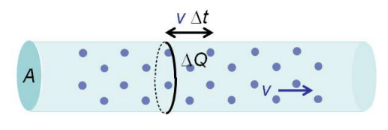
$
\begin{aligned}
I=\frac{Q}{t}=\frac{n e A d}{d / v} \\
\rightarrow \boldsymbol{I}=\boldsymbol{v} \boldsymbol{A n} \boldsymbol{e}
\end{aligned}
$
$\mathrm{n}$ – charge volume density
$\mathrm{v}$ – electron drift velocity
Example B: The cross-sectional area of a wire is $2.5 \times 10^{-6} \mathrm{~m}^2$. The density of free electrons is $n=5.0 \times 10^{28}$ electrons $/ \mathrm{m}^3$. A charge of $60 \mathrm{C}$ passes through the wire in 30 minutes. What is the drift velocity of the electrons in the wire? How long would it take the electrons to go from a light switch to a bulb $20 \mathrm{~m}$ away?
Answer/Explanation
$
\begin{aligned}
I & =V A \cap e \Rightarrow \frac{Q}{t}=v A n e \Rightarrow V=\frac{Q}{\text { Ane }} \\
\Rightarrow V & =\frac{60 C}{\left(30 \mathrm{mins} \times 60 \frac{\mathrm{s}}{\mathrm{min}}\right)\left(2.5 \times 10^{-6} \mathrm{~m}^2\right)\left(5 \times 10^{28}\right)\left(1.6 \times 10^{-19}\right)}=1.67 \times 10^{-6} \mathrm{~m} / \mathrm{s} \\
t & =\frac{20 \mathrm{~m}}{1.67 \times 10^{-6} \mathrm{~m} / \mathrm{s}}=1.2 \times 10^7 \approx 139 \text { days }
\end{aligned}
$
Electron drift velocity is very slow even though electrons move extremely fast. This is because electrons move very erratically, so they mostly move around randomly, but they move on average in the direction of current very slowly. As shown in the example, it takes a long time for a single electron to get anywhere, but the entire circuit starts moving at the same time once a circuit is closed.
- Resistivity – Resistivity is a property of the material. in metals, it is the ratio of electric field to current

density is constant:
$\rho=\frac{E}{J}$
$\mathrm{J}$ – current density
* A perfect conductor has zero resistivity. A perfect insulator has infinite resistivity.
$*$ Resistivity is the reciprocal of conductivity. Conductivity $=\mathrm{J} / \mathrm{E}$
- Resistivity and Resistance – Charge drifts in the direction of the force on it. The charge makes inelastic collisions with stationary particles and transfer energy to them. Thus, conductors get warmer as current flows.
$
\boldsymbol{R}=\frac{\rho L}{A} \quad * d R=\frac{\rho d}{A}
$
$\mathrm{R}$ – resistance
$\mathrm{L}$ – length of conductor
$\mathrm{A}$ – cross sectional area of conductorLorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Example C: A copper wire $\left(\rho=1.72 \times 10^{-8} \Omega \mathrm{m}\right.$ ) has a cross section of area $5.0 \mathrm{~mm}^2$ and carries a current of $5.0 \mathrm{~A}$. The density of free electrons in the wire is $1.0 \times 10^{29}$ electrons $/ \mathrm{m}^3$.
a) How many electrons pass through cross section of the wire per unit time?
b) What is the current density in the wire?
c) What is the drift velocity of the electrons?
d) If the wire is $10 \mathrm{~cm}$ long then what is its resistance?
e) What is the electric field in the wire?
Answer/Explanation
a) $I=5 \mathrm{~A}=5 \frac{c}{\mathrm{~s}}$ \#elections $=5 \frac{Q}{5} \times \frac{1 \text { elation }}{1.6 \times 10^{-14} \ell}=3.1 \times 10^{19}$ elections
b) $J=\frac{I}{A}=\frac{5 \mathrm{~A}}{\left(5 \times 10^{-6} \mathrm{~m}^2\right)}=1 \times 10^6 \frac{\mathrm{A}}{\mathrm{m}^2}$
c) $I=v A n e \Rightarrow V=\frac{I}{A n e}$
$\Rightarrow V=\frac{5 A}{\left(5 \times 10^{-6} \mathrm{~m}^2\right)\left(1 \times 10^{29} / \mathrm{m}^3\right)\left(1.6 \times 10^{-17} \mathrm{C}\right)}=6.3 \times 10^{-5} \mathrm{~m} / \mathrm{s}$
d) $R=\frac{\rho L}{A}=\frac{\left(1.72 \times 10^{-8} \Omega \mathrm{m}\right)(.10 \mathrm{~m})}{\left(5 \times 10^{-6} \mathrm{~m}^2\right)}=3.4 \times 10^{-4} \Omega$
e) $\rho=\frac{E}{J} \Rightarrow E=\rho J=\left(1.72 \times 10^{-8} \Omega_m\right)\left(1 \times 10^6 \frac{\mathrm{A}}{\mathrm{m}^2}\right)=.018 \frac{\mathrm{N}}{\mathrm{C}}$
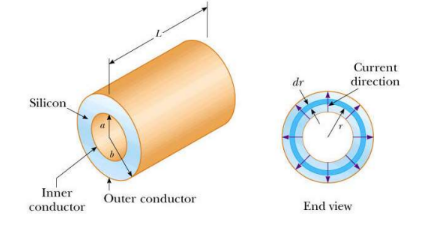
Example D: A coaxial cable consists of two concentric cylindrical conductors. The region between the conductors is filled with a plastic material. Current leakage through the plastic, in the radial direction, is unwanted. The radius of the inner conductor is a a= 0.5 cm, the radius of the outer conductor is $\mathrm{b}=1.0 \mathrm{~cm}$, and the length is $\mathrm{L}=10 \mathrm{~cm}$. The resistivity of the plastic is $1.0 \times 10^{13} \Omega m$.
Answer/Explanation
$\begin{aligned} & R=\frac{\rho L}{A} \rightarrow d R=\frac{\rho d r}{A}=\frac{\rho d r}{2 \pi r L} \\ & \rightarrow R=\int_a^b \frac{\rho}{2 \pi r L} d r=\frac{\rho}{2 \pi L} \int_a^b \frac{d r}{r}\\&R=\frac{\rho}{2 \pi L} \ln |r|_a^b=\frac{\rho}{2 \pi L} \ln \left|\frac{b}{a}\right|=\frac{1.0 \times 10^{13} \Omega m}{2 \pi(.10 \mathrm{~m})} \ln \left|\frac{.01 \mathrm{~m}}{.005 \mathrm{~m}}\right|=1.1 \times 10^{13} \Omega\end{aligned}$
A high resisitance is desirable going across the coaxial cable to prevent current leakage.
- Resistivity and Temperature
$
\Delta \rho=\rho_0 \alpha \Delta T \quad \rightarrow \rho=\rho_0(1+\alpha \Delta T)
$
$\alpha$-temperature coefficient of resistivity, fractional change of resistivity per degree
$\Delta \rho / \rho_0$ – fractional change in resistivity
Since resistance varies directly with resistivity, the following is also true: $\Delta R=R_0 \alpha \Delta T$
*Resistivity of a semiconductor decreases rapidly with temperature.
Example E: Another copper wire $\left(\alpha=.00393 /{ }^{\circ} \mathrm{C}\right)$ has a resistance of $.01 \Omega$ at $20^{\circ} \mathrm{C}$. What is it resistance at $100^{\circ} \mathrm{C}$ ?
Answer/Explanation
$
\Delta R=R_0 \alpha \Delta T \rightarrow R=R_0(1+\alpha \Delta T)=(.01 \Omega)\left(1+\left(.00393 \frac{1}{\rho^{\mathrm{C}}}\right)\left(80^{\circ} \mathrm{C}\right)=. \mathbf{0 1 3} \Omega\right.
$
Power
- A charge moves through an element as shown. The electric field does work on the charge as it passes through
- $
\boldsymbol{W}=\boldsymbol{V} \boldsymbol{q}
$ - Power
$
\begin{aligned}
\text { Power } & =\frac{\text { Work }}{\text { time }}=\frac{V q}{t}=V\left(\frac{q}{t}\right) \\
& \text { – } P=V I
\end{aligned}
$
- Using Ohm’s Law with the power equation above, you can also derive the following two expressions for power:
- $P=I^2 R=\frac{V^2}{R}$
How power is used
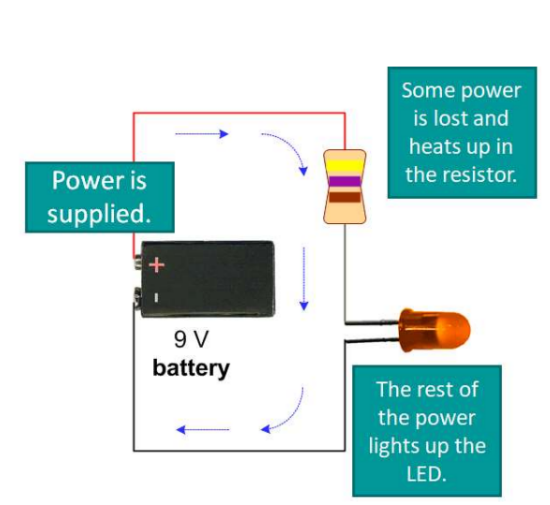
How power is used
- Sources – “Supply” power; $\mathbf{P}>0$
- Loads (lightbulbs, etc.) – Use power, $\mathbf{P}<0$
*more current $=$ more power, makes bulbs brighter. “more flow $=$ more glow” - Resistors and wires – “Dissipate” Power, power is lost to heat. $\mathrm{P}<0$
Example F: Describe why a lightbulb will be less bright over time.
Answer/Explanation
Over time, a lightbulb will get hotter, which will increase the resistance of the bulb. As the resistance increase, the current will decrease. Less current will mean less power and therefore less brightness in the bulb.
Example G: A 90 W stereo is connected to a 120 V source. If energy cost $.10 per kilowatt-hour, find how much it will cost to leave the stereo on for two days straight playing nothing but “Africa” by Toto on repeat.
Answer/Explanation
Cost $=90 \times 5 \times \frac{1 \mathrm{~kW}}{1000 \times \pi} \times 2$ dags $\times \frac{24 \mathrm{he}}{1 \mathrm{deg}} \times 81.10 \mathrm{kuth}=\$ 5.4$